Семантика традиционной силлогистики
Для начала необходимо выделить и определить некоторый универсум рассуждения U. Истинность категорических атрибутивных высказываний можно определить в традиционной силлогистике через выполнимость для субъектов и предикатов отношений, задаваемых некоторыми модельными схемами.
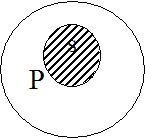
1. Предложение «Всякий S есть Р» истинно тогда и только тогда, когда классы S и Р находятся в одном из следующих отношений:
№ 1 № 2
|
|
Например, «Всякий квадрат – это равносторонний прямоугольник» находится в отношении, задаваемом первой модельной схемой, и, следовательно, является истинным. «Всякий студент является учащимся» также является истинным, так как субъект и предикат этого высказывания находятся в отношении, задаваемом второй модельной схемой.
2. Предложение «Ни один S не есть Р» истинно тогда и только тогда, когда классы S и Р находятся в одном из следующих отношений:
№ 1 № 2
 |  |
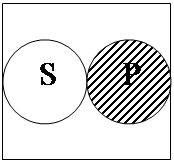Примером истинного предложения, в котором субъект и предикат находятся в отношении, задаваемом первой модельной схемой, может служить предложение «Всякий юридически наказуемый поступок не есть преступление». Вторая модельная схема имеет место для субъекта и предиката предложения «Ни одно натуральное число не является иррациональным», и поэтому оно истинно.
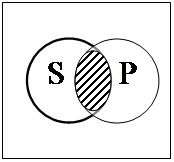
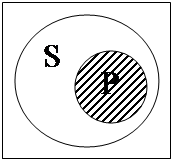
3. Предложение «Некоторый S есть Р» истинно тогда и только тогда, когда S и Р находятся в одном из следующих отношений:
№ 1 № 2
|
|
№ 3 № 4
 |  |
№ 5
Примерами высказываний, субъекты и предикаты которых соответственно удовлетворяют каждой из данных модельных схем, будут: 1) «Некоторый квадрат есть равносторонний прямоугольник», 2) «Некоторые студенты являются учащимися», 3) «Некоторый учащийся – спортсмен», 4) «Некоторый писатель является поэтом», 5) «Некоторое натуральное число, меньше 100, является натуральным числом, большим 80».
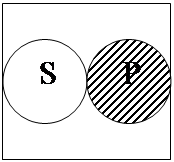
4. Предложение «Некоторый S не есть Р» истинно тогда и только тогда, когда классы S и Р находятся в одном из следующих отношений:
№ 1 № 2
| |
|
 |
№ 3 № 4
| |  |
№ 5
№ 5
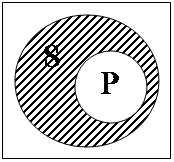
Примерами соответствующих высказываний для каждой модельной схемы будут высказывания: 1) «Некоторое натуральное число, меньшее 100, не является натуральным числом, большим 80», 2) «Некоторый учащийся не является спортсменом», 3) «Некоторый юридически ненаказуемый поступок не есть преступление», 4) «Некоторое натуральное число не является иррациональным», 5) «Некоторый писатель не является поэтом».
5. Предложение «а есть Р» истинно тогда и только тогда, когда между предметом, обозначенным термином «а», и классом Р существует отношение, соответствующее схеме №1:
Это значит, что предмет а является элементом класса Р. Например: «Д.И.Менделеев – химик», «2 – четное число», «Лондон – город» и т.д.
6. Предложение «а не есть Р» истинно тогда и только тогда, когда между предметом, обозначенным термином «а», и классом Р существует отношение, соответствующее схеме №2:
№ 1 № 2
 |  |
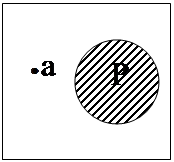Это значит, что предмет а не является элементом класса Р. Например: «5 не является четным числом», «Наполеон не является англичанином» и др.