Для автомата Мура кодировка выходных сигналов не требуется, так как они однозначно связаны с состоянием, а следовательно и с кодами этих состояний

Задание 2.1

Построить цифровой автомат заданного типа (Мили или Мура) для заданной ГСА, используя заданный тип триггера (RS-, D-, T-триггер). Тип автомата, номер ГСА (соответствует номеру рисунка, на котором она находится) и тип триггера выбирается из табл.2.

Тип триггера (ТТ), тип цифрового автомата (ТЦА), номер ГСА (ГСА) задается колонками, соответственно, 1,2 и 3.

Номер варианта определяется последними двумя цифрами зачетной книжки (равен 11).

№	Задание 2.1
вар	ТТ	ТЦА	ГСА
	RS	Мура	Рис.1

Исходная схема (рис. 1)

Решение:

Кодирование входных сигналов выполним через набор логических переменных «х». Множество входных сигналов включает три элемента. Поэтому для представления каждой из них достаточно использовать комбинации из двух переменных х₁, х₂. Кодировка входных переменных представлена таблицей 2.

Таблица1.

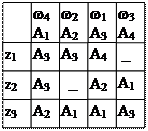
Кодирование состояний выполним через набор логических переменных «Q». Множество состояний включает четыре элемента. Поэтому для представления каждой из них достаточно использовать комбинации из двух переменных Q₁, Q₂. Кодировка состояний представлена в таблице 2. Кодировка входных переменных представлена в таблице 3.

Табл.3 Табл.2

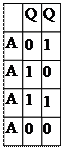Для автомата Мура кодировка выходных сигналов не требуется, так как они однозначно связаны с состоянием, а, следовательно, и с кодами этих состояний.

	Начало	Конец
N	An	Q1Q2Q3Q4	An	Q1Q2Q3Q4	Условие	Выход	qs1 qr1 qs2 qr2 qs3 qr3 qs4 qr4
	A0	0 0 0 0	A1	0 0 0 1	x5	y5y1	0 1 0 1 0 1 1 0
			A3	0 0 1 1	~x5	y11y41y96	0 1 0 1 1 0 1 0
	A1	0 0 0 1	A2	0 0 1 0		y17	0 1 0 1 1 0 0 1
	A2	0 0 1 0	A6	0 1 1 0	x3	y1	0 1 1 0 1 0 0 1
			A5	0 1 0 1	~x3	y22	0 1 1 0 0 1 1 0
	A3	0 0 1 1	A5	0 1 0 1	x11	y22	0 1 1 0 0 1 1 0
			A4	0 1 0 0	~x11	yn	0 1 1 0 0 1 0 1
	A4	0 1 0 0	A5	0 1 0 1	x4	y22	0 1 1 0 0 1 1 0
	A5	0 1 0 1	A7	0 1 1 1	~x9	yn	0 1 1 0 1 0 1 0
		0 1 0 1	A1	0 0 0 1	X9 x10	Y5 y1	0 1 0 1 0 1 1 0
			A8	1 0 0 0	X9 ~x10	Y4	1 0 0 1 0 1 0 1
	A6	0 1 1 0	A7	0 1 1 1	~x9	yn	0 1 1 0 1 0 1 0
			A8	1 0 0 0	X9 ~x10	Y4	1 0 0 1 0 1 0 1
	A7	0 1 1 1	A5	0 1 0 1		Y22	0 1 1 0 0 1 1 0
	A8	1 0 0 0	A9	1 0 0 1		Y13 y18 yk	1 0 0 1 0 1 1 0
	__ __ __
y5=	Q1Q2Q3Q4
	__ __ __	__ __
Y1=	Q1Q2Q3Q4	+Q1Q2Q3Q4
	__ __
y11=	Q1Q2Q3Q4
	__ __
y41=	Q1Q2Q3Q4
	__ __
y96=	Q1Q2Q3Q4
	__ __ __
y17=	Q1Q2Q3Q4
	__ __
y22=	Q1Q2Q3Q4
	__ __ __
y4=	Q1Q2Q3Q4
	__ __
y13=	Q1Q2Q3Q4
	__ __
y18=	Q1Q2Q3Q4
	__ __
yk=	Q1Q2Q3Q4

qr1= Q1Q2Q3Q4x5+ Q1Q2Q3Q4x5+ Q1Q2Q3Q4+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x11+

Q1Q2Q3Q4x11+ Q1Q2Q3Q4x9+ Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4x9+ Q1Q2Q3Q4(1,2,3,4,5,6,7,8,9,10,12,14)

qs1= Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4(11,13,15)

qs2 = Q1Q2Q3Q4x3+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x11+ Q1Q2Q3Q4x9+ Q1Q2Q3Q4 (4,5,6,7,8,9,12,14)

qr2 = Q1Q2Q3Q4x5+ Q1Q2Q3Q4x5+ Q1Q2Q3Q4+ Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4x9x10+ Q1Q2Q3Q4 (1,2,3,10,11,13,15)

qs3 = Q1Q2Q3Q4x5+ Q1Q2Q3Q4+ Q1Q2Q3Q4x3+ Q1Q2Q3Q4x9(2,3,5,9,12)

qr3=Q1Q2Q3Q4x5+Q1Q2Q3Q4x3+Q1Q2Q3Q4x11+Q1Q2Q3Q4x11+Q1Q2Q3Q4x9x10+Q1Q2Q3Q4x9x10+Q1Q2Q3Q4+Q1Q2Q3Q4(1,4,6,7,8,10,11,13,14,15)

qs4=Q1Q2Q3Q4x5+Q1Q2Q3Q4x5+Q1Q2Q3Q4x3+Q1Q2Q3Q4x11+Q1Q2Q3Q4x9+Q1Q2Q3Q4x9x10+Q1Q2Q3Q4+Q1Q2Q3Q4(1,2,4,7,8,9,10,12,14,15)

qr4=Q1Q2Q3Q4+Q1Q2Q3Q4x3+Q1Q2Q3Q4x11+Q1Q2Q3Q4x9x10(3,5,6,11,13)

Схема автомата:

Тип 3.5.

Синтез автомата Мура.

Задача.

Синтезировать цифровой автомат, заданный в виде таблиц 1.

Память автомата построить на RS-триггере. При синтезе логических выражений использовать логический базис И, ИЛИ, НЕ.

Решение

Кодирование входных сигналов выполним через набор логических переменных «х». Множество входных сигналов включает три элемента. Поэтому для представления каждой из них достаточно использовать комбинации из двух переменных х₁, х₂. Кодировка входных переменных представлена таблицей 2.

Таблица1.

Кодирование состояний выполним через набор логических переменных «Q». Множество состояний включает четыре элемента. Поэтому для представления каждой из них достаточно использовать комбинации из двух переменных Q₁, Q₂. Кодировка состояний представлена в таблице 2. Кодировка входных переменных представлена в таблице 3.

Табл.3 Табл.2

Для автомата Мура кодировка выходных сигналов не требуется, так как они однозначно связаны с состоянием, а следовательно и с кодами этих состояний.

Таблица 1 после замены переменных исходного задания цифрового автомата на их кодированные значения будут иметь вид, приведенный в таблице 4.

Таблица 4

				-
		-

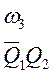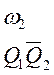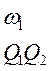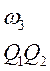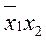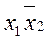В таблице 4 клетки заполнены двухразрядным кодом, первый разряд которого отображает значение переменной Q₁, а вторая - переменную Q₂(«1» - переменная имеет прямое значение, «0» - переменная имеет обратное значение).

Для управления памятью на RS- триггере, необходимо для первого и второго триггера, на которых строится память синтезируемого цифрового автомата, сформировать сигналы установки «1» (q_S) и установки «0» (q_R ).

Логические выражения для этих сигналов, составленные на основе таблицы 4, имеют вид:

.

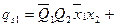
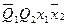
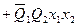
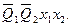
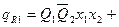
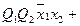
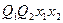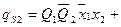
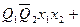
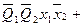
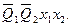
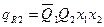
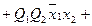
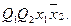
Приведенные выражения формируются следующим образом:

- в дизъюнктивном выражении для q_Si используются конъюнкции, определяющие клетки таблицы, соответствующие случаям, когда в исходном коде состояния i-ый разряд имел значение «0», а конечном - «1»;

- в дизъюнктивном выражении для q_Ri используются конъюнкции, определяющие клетки таблицы, соответствующие случаям, когда в исходном коде состояния i-ый разряд имел значение «1», а конечном - «0».

Для более компактного представления полученных логических выражений и обозначений на формируемой схеме цифрового автомата, введем десятичную кодировку конъюнкций, используемых в полученных логических выражениях. Каждая конъюнкция представляет набор одних и тех же переменных Q₁, Q₂, x₁, x₂, поэтому представление конъюнкций можно рассматривать как четырехразрядный двоичный код и кодировать их десятичными эквивалентами этого двоичного кода. Таким образом, ранее полученные выражения можно представить в следующей компактной форме:

q_S1 = 5+6+7+3; q_R1 = 11+13+15.

q_S2 = 9+11+2+3; q_R2= 7 +13+14.

Таким образом множество неповторяющихся конъюнкций в кодированной форме, которые используются во всех составленных логических выражениях и которые нужно сформировать при построении схемы цифрового автомата, имеет вид:

{2,3,5, 6,7,9,11,13,14,15}.

.Логические выражения для выходных сигналов, исходя из таблицы 3 и 4, имеют вид:

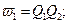
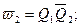
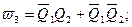
Сигнал w₃ имеет место при двух состояниях цифрового автомата, поэтому соответствующее ему логическое выражение представляет собой дизъюнкцию двух конъюнкций, отражающих коды этих двух состояний автомата.

Схема, реализующая заданный цифровой автомат, включая кодировку входных сигналов, его память, логические схемы, реализующие логические выражения для управления памятью и выработки выходных сигналов, приведена на рис. 1.

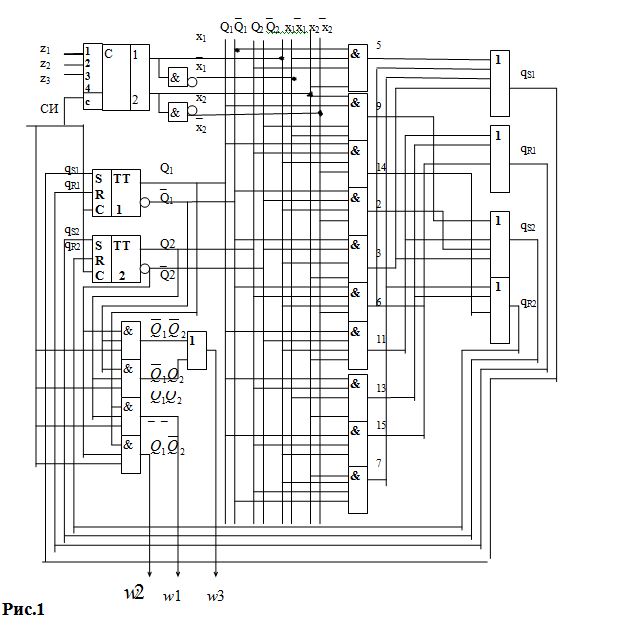
Рис.1