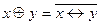Логические операции над высказываниями
Понятие высказывания
Основным (неопределяемым) понятием математической логики является понятие простого высказывания..
Определение.Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем- либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются истина и .ложь.
Приведем примеры высказываний.
1) Новгород стоит на Волхове.
2) Париж - столица Англии.
3) Карась не рыба.
4) Число 6 делится на 2 и на 3.
5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.
Высказывания 1), 4), 5) истинны. а высказывания 2) и 3) ложны.
Очевидно, предложение Да здравствуют наши спортсмены!,» не является высказыванием.
Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).
Высказывания, которые получаются из элементарных с помощью грамматических связок НЕ, И, ИЛИ., .ЕСЛИ .... ТО ..... ТОГДА И ТОЛЬКО ТОГДА.. принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания Карась - рыба. с помощью
отрицания НЕ, высказывание 4) образовано из элементарных высказываний Число 6 делится на 2., 4 Число 6 делится на 3, соединенных союзом И.. Высказывание 5) получается из простых высказываний Юноша окончил среднюю школу, .Юноша получает аттестат зрелости. с помощью грамматической связки .ЕСЛИ ..., ТО ..... Сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок .ИЛИ., .ТОГДА И ТОЛЬКО ТОГДА..
В алгебре логики все высказывания рассматриваются только С точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно. либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
В дальнейшем будем элементарные высказывания обозначать малыми буквами латинского алфавита: х. у, z, .... а, b. с, ...; истинное значение высказывания цифрой 1, а ложное значение цифрой 0.
Если высказывание а истинно. то будем писать а = 1 , а если а ложно, то а = 0 .
Логические операции над высказываниями.
1. Отрицание. Отрицанием высказывания х называется новое высказывание 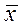 , которое истинно тогда и только тогда, когда х ложно, и ложно, если высказывание х истинно.
, которое истинно тогда и только тогда, когда х ложно, и ложно, если высказывание х истинно.
| х | 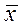 |
2. Конъюнкция (логическое умножение). Конъюнкцией двух высказываний х и у называется новое высказывание 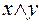 , которое считается истинным, если оба высказывания х и у истинны, и ложным во всех остальных случаях.
, которое считается истинным, если оба высказывания х и у истинны, и ложным во всех остальных случаях.
Таблица истинности операции конъюнкции имеет следующий вид:
| х | у | 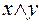 |
3. Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний х и у называется новое высказывание 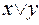 , которое считается ложным, если оба высказывания х и у ложны, и истинным во всех остальных случаях.
, которое считается ложным, если оба высказывания х и у ложны, и истинным во всех остальных случаях.
Эту операцию наглядно можно изобразить с помощью таблицы истинности:
| х | у | 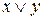 |
4. Импликация.Импликацией двух высказываний х и у называет новое высказывание 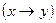 , которое считается ложным, если х- истинно, а у- ложно, и истинным во всех остальных случаях.
, которое считается ложным, если х- истинно, а у- ложно, и истинным во всех остальных случаях.
Высказывание х называют посылкой, а у – заключением.
Таблица истинности имеет следующий вид:
| х | у | 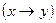 |
5. Эквиваленция.Эквиваленцией двух высказываний х и у называют новое высказывание 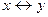 , которое считается истинным, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны..
, которое считается истинным, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны..
Эту операцию наглядно можно изобразить с помощью таблицы истинности.
| х | у | 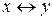 |
Символы 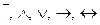 называются позиционными связками. Логическим связкам приписывают ранги в следующем порядке убывания старшинства:
называются позиционными связками. Логическим связкам приписывают ранги в следующем порядке убывания старшинства: 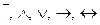 . Таким образом, связка более высокого ранга имеет большую область действия.
. Таким образом, связка более высокого ранга имеет большую область действия.
Существуют операции, с помощью которых может быть выражена любая из пяти логических операций, рассмотренных выше. Такими операциями являются:
1. Штрих Шеффера (читается «А несовместно с В»). Эта операция обозначается 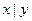 и определяется следующей таблицей истинности.
и определяется следующей таблицей истинности.
| x | y | 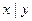 |
Имеет место следующее равенство 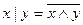
2. Стрелка Пирса(читается «ни А, ни В»). Эта операция обозначается 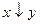 и определяется следующей таблицей истинности.
и определяется следующей таблицей истинности.
| x | y | 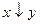 |
Имеет место следующее равенство 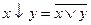
3. Сложение по модулю два (исключающее или). Эта операция обозначается 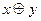 и определяется следующей таблицей истинности.
и определяется следующей таблицей истинности.
| x | y | 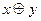 |
Имеет место следующее равенство