Правила построения косвенного (апагогического) доказательства

Косвенное доказательство формулы (*) строится согласно следующему предписанию.

На любом шаге построения можно написать:

1) одну из формул 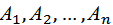в качестве допущения;

1а) формулу противоречащую формуле С;

2) формулу, следующую из ранее написанных форм по одному из правил логического следования;

3) ранее доказанную формулу.

Косвенное доказательство формулы (*) считается построенным, если в соответствии с пп. 1)-3), включая и п. 1а), получена последовательность формул, содержащая пару противоречащих формул и оканчивающаяся одной из них.

Пример. Докажем формулу

~q→~(q&p)

Доказательство.

1. ~q – допущение;

2. q&p – допущение косв. док-ва;

3. q – УК (2)

Противоречие: 1,3.

Пример. Докажем формулу

(~p→p)→p

Доказательство.

1. ~p→p – допущение;

2. ~p – допущение косв. док-ва;

3. p – МП (1,2);

Противоречие: 2, 3.

Пример. Докажем формулу

(~p→q)→((~p→~q)→p)

Доказательство

1.~p→q – допущение;

2. ~p→~q – допущение;

3. ~p – допущение косв. док-ва;

4. q – МП (1,3);

5. ~q – МП (2,3);

Противоречие: 4, 5.

Доказательство в системе N связано с конечной системой, или совокупностью доказательств, упорядоченных некоторым естественным образом.

Завершая описание системы N, мы введём следующее определение доказуемой формулы. Формула называется доказуемой формулой, или логической теоремой (системы N), если можно построить доказательство данной формулы (по правилам системы N).

Кроме того, мы принимаем следующее определение знака эквивалентности:

.

Оно означает, что выражение, стоящее слева от знака (знака равенства по определению), рассматривается как сокращённая запись выражения, стоящего справа от этого знака. Согласно данному определению, если в формуле имеется вхождение выражения из правой части данного определения, то его можно заменять на вхождение выражения из его левой части (и наоборот).

Из определения знака ↔ непосредственно следует, что правила

A→B B→A – введение эквивалентности (ВЭ)

A↔B

A↔B – удаление эквивалентности (УЭ);

A→B

A↔B – удаление эквивалентности (УЭ)

B→A

представляют собой частные случаи правил ВК и УК.

Логические средства, используемые в исчислении высказываний для построения рассуждений, являются слишком бедными, чтобы с их помощью можно было описать всё многообразие различных приёмов, применяемых в процедурах дедукции в конкретных науках и повседневной жизни. Эти средства ограничены бедностью языка исчисления высказываний, в котором простые предложения трактуются как не имеющие внутренней структуры. С этой точки зрения язык исчисления предикатов обладает гораздо большими выразительными возможностями и позволяет анализировать и изучать такие рассуждения, которые зависят от внутренней структуры простых предложений.

В исчислении предикатов сохраняются все правила вывода исчисления высказываний, но к ним теперь надо присоединить новые правила, позволяющие оперировать с кванторами.

Кванторные правила вывода:

– введение всеобщности (ВВ);

- удаление всеобщности (УВ);

введение существования (ВС);

– удаление существования (УС).

С

А, С– формулы, x, y – переменные, -результат корректной подстановки y в А вместо х.

Ограничения на применение правил «введения всеобщности» и «удаление существования».

1. При построении доказательства правило введения всеобщности применяется, если выполняются следующие условия:

а) собственная переменная данного правила не входит свободно в формулы, написанные ранее в качестве допущений;

б) собственная переменная не входит свободно в формулу, обозначенную в схеме правила посредством .

2. При построении доказательства правило «устранение существования» применяется, если выполняются следующие условия:

а) собственная переменная данного правила не входит свободно в формулы, ранее написанные в качестве допущений;

б) собственная переменная не входит свободно ни в формулу, обозначенную посредством , ни в формулу, обозначенную посредством С, в схеме правила УС (т.е. ни в левую посылку, ни в заключение данного правила).

Покажем, как строится доказательство формулы логики предикатов.

Пример. Следует доказать в системе естественного вывода логики предикатов формулу

Доказательство.

1. – допущение;

2. – допущение;

3. A→B – УВ (1);

4. A – УВ (2);

5. В – МП (3,4);

– ВВ (5).

Пример. Следует доказать в системе естественного вывода логики предикатов формулу

Доказательство.

1. –допущение;

2. – допущение;

3. A→B – УВ (1);

4. B – УС (2,3);

– ВС (4).

Хотя исчисление предикатов представляет собой семантически полную логическую теорию, оно не является разрешимой теорией. Для исчисления предикатов не существует эффективного метода, позволяющего ответить на вопрос, доказуема или нет произвольная формула данного исчисления.

Контрольные вопросы:

1. В чём разница между формальными и формализованными теориями?

2. Дайте определение системы естественного вывода.

3. Что такое кратная импликация?

4. Какие ограничения существуют на применение правил «введения всеобщности» и «удаления существования»?

5. Как соотносятся вывод и доказательство?

6. В чём состоит отличие между построением прямого доказательства и построением косвенного доказательства?

7. Что такое антецедент и консеквент?

8. В чём заключается преимущество исчисления предикатов по отношению к исчислению высказываний?

Тема 11. Силлогистика

Изучив материалы темы, Вы сможете:

- понять структуру простого категорического силлогизма;

- определить вид силлогизма со сложными суждениями;

- показать в чём состоит отличие между фигурами простого категорического силлогизма;

- восстановить любую энтимему;

- определить разницу между соритом и полисиллогизмом;

- узнать возможности и недостатки силлогизма.

Любое умозаключение можно определить как такую мыслительную структуру, в которой из двух или более истинных исходных суждений, называемых посылками, на основании определенной логической связи между ними, формируется новое истинное суждение, называемое заключением.

По направленности движения мысли умозаключения подразделяют на дедуктивные и индуктивные. Особенность всех дедуктивных умозаключений является то, что они дают истинностное знание. Индуктивные умозаключения дают не истинностное, а только вероятное знание (за исключением полной индукции, которая дает истинностное знание).

Поскольку термины простых категорических суждений могут рассматриваться в логических рассуждениях либо в качестве элементарных, либо в качестве сложных образований, постольку в рамках традиционной силлогистики выделяют позитивную традиционную силлогистику и негативную традиционную силлогистику.

Первая из них не учитывает внутреннюю структуру терминов, трактует субъект и предикат как элементарные выражения, неразложимые на составные части.

В суждении «Ни одно чётное число не является нечётным» предикатом считается имя «являющийся нечётным», т. е. имя «нечётный» берётся без учёта выраженного частицей «не» смысла (терминного отрицания). Если же этот смысл оказывается выявленным, учтённым в структуре высказывания, то в приведённом выше примере предикатом будет считаться имя «являющийся чётным», взятое с отрицанием. Обозначив терминное отрицание символом «-», получим запись:

«Ни один S не есть -P».

Необходимо отметить, что к позитивной силлогистике, как правило, относят такой вид непосредственного умозаключения, как обращение, а к негативной силлогистике такие виды непосредственного умозаключения как превращение, противопоставление субъекту, противопоставление предикату. Все эти виды умозаключений будут рассмотрены ниже.

Для всех видов силлогистики большое значение имеет распределённость терминов. Распределённым называется термин, взятый в полном объёме.

№ п/п	Вид суждения	S	P
1.	A	+	– (+)
2.	I	–	– (+)
3.	E	+	+
4.	O	–	+

В таблице «+» обозначает то, что термин распределён, а «–» обозначает то, что термин нераспределён.

Например, общеутвердительное суждение (A): «Все люди являются разумными существами». Люди – субъект (S), разумные существа – предикат (P). Схема отношений между S и P в этом суждении будет такой:

Так как субъект (S) и предикат (P) находятся в отношении тождества, то они оба распределены.

Общеутвердительное суждение (A): «Все стоматологи – врачи». Стоматологи – субъект (S), врачи – предикат (P). Схема отношений между S и P в этом суждении будет такой:

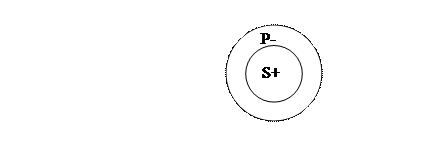
При этом субъект (S) будет распределён, т. е. взят в полном объёме, а предикат (P) нераспределён.

Общеотрицательное суждение (E) «Ни один человек не является пресмыкающимся». Человек – субъект (S), пресмыкающееся – предикат (P). Схема отношений между S и P в этом суждении будет такой:

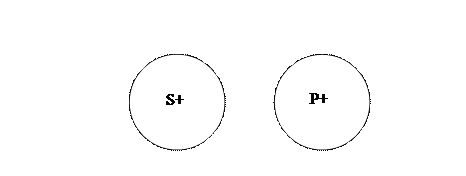
В данном примере и субъект (S) и предикат (P) распределены.

Частноутвердительное суждение (I): «Некоторые учащиеся являются школьниками». Учащиеся – субъект (S), школьники – предикат (P). Схема отношений между S и P в этом суждении будет такой:

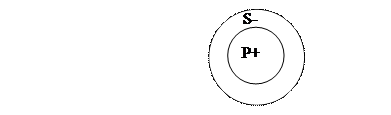
В этом примере субъект (S) нераспределён, а предикат (P) распределён.

Частноутвердительное суждение (I) «Некоторые люди являются умеющими плавать». Люди – субъект (S), умеющие плавать – предикат (P). Схема отношений между S и P в этом суждении будет такой:

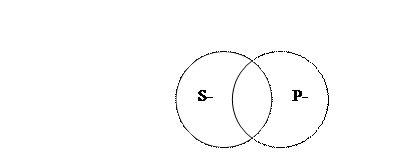
В этом примере и субъект (S) и предикат (P) нераспределены. Здесь нас интересует та часть объёма, которая включает в себя людей, которые при этом являются умеющими плавать.

Примечательно, что если мы суждение из последнего примера преобразуем в частноотрицательное, то схема отношений между субъектом и предикатом будет та же, а распределённость терминов будет иная.

«Некоторые люди не являются умеющими плавать» – частноотрицательное суждение (O). Люди – субъект (S), умеющие плавать – предикат (P). Схема отношений между S и P в этом суждении будет такой:

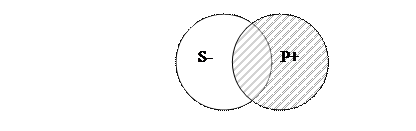
В данном примере субъект (S) нераспределён, а предикат (P) распределён. Нас интересует та часть объёма S, в которую входят люди не являющиеся умеющими плавать.

Для частноотрицательного суждения характерна ещё одна схема отношений между субъектом и предикатом.

«Некоторые растения являются цветами» – частноотрицательное суждение (O). Растения – субъект (S), цветы – предикат (P). Схема отношений между S и P в этом суждении будет такой:

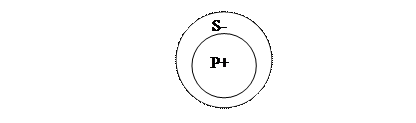
Самым простым видом умозаключения является непосредственное умозаключение. Непосредственное умозаключение – умозаключение, в котором вывод строится на основе лишь одной посылки. К непосредственным видам умозаключения относятся: превращение, обращение, противопоставление предикату (субъекту).

Превращение – умозаключение, при котором изменяется качество посылки при одновременной замене предиката на противоречащий ему термин.

1) Превращение общеутвердительного суждения:

A: Все S есть P

E: Ни одно S не есть не P

Все осины являются деревьями

Ни одна осина не является не деревом

2) Превращение общеотрицательного суждения:

E: Ни одно S не есть P

A: Все S есть не P

Ни один соловей не является вороной

Все соловьи являются не воронами

3) Превращение частноутвердительного суждения:

I: Некоторые S есть P

O: Некоторые S не есть не P

Некоторые люди являются коллекционерами

Некоторые люди не являются не коллекционерами

4) Превращение частноотрицательного суждения:

O: Некоторые S не есть P

I: Некоторые S есть не P

Некоторые художники не являются импрессионистами

Некоторые художники являются не импрессионистами

Обращение – умозаключение, при котором происходит замена субъекта предикатом, а предиката субъектом при сохранении качества суждения. Обращение бывает двух видов: обращение чистое и обращение с ограничением. Чистое обращение – обращение, при котором не меняется количество исходного суждения. Обращение с ограничением – это обращение, при котором меняется количество исходного суждения.

1) Обращение общеутвердительного суждения (с ограничением):

A: Все S есть P

I: Некоторые P есть S

Все белые медведи являются медведями

Некоторые медведи являются белыми медведями

Обращение общеутвердительного суждения (чистое):

A: Все S есть P

A: Все P есть S

Все люди является разумными существами

Все разумные существа является людьми

2) Обращение общеотрицательного суждения (чистое):

E: Ни одно S не есть P

E: Ни одно P не есть S

Ни один студент не является школьником

Ни один школьник не является студентом

3) Обращение частноутвердительного суждения (чистое):

I: Некоторые S есть P

I: Некоторые P есть S

Некоторые книги являются полезными

Некоторые полезные вещи являются книгами

Обращение частноутвердительного суждения (с ограничением):

I: Некоторые S есть P

A: Все P есть S

Некоторые юристы являются следователями

Все следователи являются юристами

4) Обращение частноотрицательного суждения невозможно.

Противопоставление предикату (субъекту) – умозаключение, в котором субъектом (предикатом) заключения является термин, противоречащий предикату (субъекту) посылки, а предикатом (субъектом) – субъект (предикат) посылки. Противопоставление включает в себя превращение и обращение. Общие суждения можно противопоставить и S и P. Частные суждения можно противопоставить или только S или только P.

1) Противопоставление общеутвердительного суждения:

«Все гладиолусы являются цветами»

Противопоставление S (сначала применяем операцию обращения, затем операцию превращения):

A: Все S есть P

I: Некоторые P есть S

O: Некоторые P не есть не S

Все гладиолусы являются цветами

Некоторые цветы являются гладиолусами

Некоторые цветы не являются не гладиолусами

Противопоставление P (сначала применяем операцию превращения, затем операцию обращения):

A: Все S есть P

E: Ни одно S не есть не P

E: Ни одно не P не есть S

Все гладиолусы являются цветами

Ни один гладиолус не является не цветком

Ни один не цветок не является гладиолусом

2) Противопоставление общеотрицательного суждения:

«Ни один православный не является мусульманином»

Противопоставление S (сначала применяем операцию обращения, затем операцию превращения):

E: Ни одно S не есть P

E: Ни одно P не есть S

A: Все P есть не S

Ни один православный не является мусульманином

Ни один мусульманин не является православным

Все мусульмане являются не православными

Противопоставление P (сначала применяем операцию превращения, затем операцию обращения):

E: Ни одно S не есть P

A: Все S есть не P

I: Некоторые не P есть S

Ни один православный не является мусульманином

Все православные являются не мусульманами

Некоторые не мусульмане являются православными

3) Противопоставление частноотрицательного суждения:

«Некоторые люди не являются здравомыслящими»

Противопоставление P (сначала применяем операцию превращения, затем операцию обращения):

O: Некоторые S не есть P

I: Некоторые S есть не P

I: Некоторые не P есть S

Некоторые люди не являются здравомыслящими

Некоторые люди являются не здравомыслящими

Некоторые не здравомыслящие являются людьми

Противопоставление S невозможно.

4) Противопоставление частноутвердительного суждения:

«Некоторые грибы являются мухоморами»

Противопоставление S (сначала применяем операцию обращения, затем операцию превращения):

I: Некоторые S есть P

A: Все P есть S

E: Ни одно P не есть не S

Некоторые грибы являются мухоморами

Все мухоморы являются грибами

Ни один мухомор не является не грибом

Противопоставление P невозможно.

Невозможность противопоставления частноотрицательного суждения субъекту (S) и частноутвердительного суждения предикату (P) связана с тем, что на определённом этапе преобразований возникает необходимость обратить частноотрицательное суждение, а это невозможно.

Более сложными по своей структуре являются дедуктивные умозаключения или силлогизмы.

Среди дедуктивных умозаключений различают простой категорический силлогизм, чисто условный силлогизм, условно-категорический силлогизм, чисто разделительный силлогизм, разделительно-категорический силлогизм и условно-разделительный силлогизм. Заметим, что получение истинного вывода в большинстве названных силлогизмов – тривиальная задача. Исключение составляют только простой категорический и условно-категорический силлогизмы.

Простой категорический силлогизм - умозаключение, в котором из двух категорических суждений выводится третье категорическое суждение, термины которого связаны определённым отношением с термином, общим для обеих посылок. Простой категорический силлогизм состоит из трех категорических суждений и включает в себя средний «М», больший «Р» и меньший термины «S». Больший термин (P) – предикат заключения, содержится в большей посылке, которая находится на первом месте. Меньший термин (S) – субъект заключения, содержится в меньшей посылке, стоящей на втором месте. Средний термин (M) – термин, который содержится в обеих посылках, но не содержится в заключении. В простом категорическом силлогизме существуют четыре фигуры, которые определяются местоположением среднего термина. Фигура – это разновидность силлогизма в зависимости от местоположения среднего термина.

I фигура II фигура III фигура IV фигура

Пример силлогизма, построенного по I фигуре:

Все христиане – верующие

Все католики – христиане

Все католики – верующие

Пример силлогизма, построенного по II фигуре:

Ни один кашалот не является рыбой

Некоторые живые существа являются рыбами

Некоторые живые существа не являются кашалотами

Пример силлогизма, построенного по III фигуре:

Некоторые студенты являются талантливыми

Все студенты – учащиеся

Некоторые учащиеся являются талантливыми

Пример силлогизма, построенного по IV фигуре:

Все танкисты – военные

Все военные дают присягу

Некоторые дающие присягу люди, являются военными

В простом категорическом силлогизме существуют 256 модусов, которые зависят от количественно-качественных характеристик посылок и заключения. Из 256 теоретически возможных модусов правильными, т.е. дающими истинное заключение, являются 19. Поэтому далеко не всегда заключение следует из посылок. Например, следующие рассуждения дают ложный вывод: «Все планеты – шарообразны. Земля тоже шарообразна. Значит, она планета»; «Ни один бог не есть человек, а все люди – смертны. Значит, все смертные не есть боги». А в рассуждении «Некоторые поэты XIX века – декабристы. Некоторые друзья Пушкина – поэты XIX века. Значит, некоторые друзья Пушкина – декабристы» вывод фактически является истинным, но он не следует из посылок.

Существуют соответствующие правилапростого категорического силлогизма, соблюдения которых гарантирует истинность вывода. Общие правила силлогизма, включающие в себя правила терминов и правила посылок, распространяются на все фигуры силлогизма. Кроме того, есть специальные правила для каждой фигуры силлогизма.

Правила терминов:

1. Силлогизм должен содержать только три термина.

Пример:

Материя – вечна

Ситец – материя

Ситец – вечен

Слово «материя» используется в разных смыслах, поэтому в данном силлогизме не три термина, а четыре. Данная ошибка представляет собой частный случай нарушения закона тождества.

2. Средний термин должен быть распределён хотя бы в одной из посылок.

Пример:

Некоторые животные являются привередливыми

Кошки – животные

?

Из этих двух посылок нельзя вывести заключение, потому что средний термин «животные» нераспределен как в большей посылке (в частноутвердительном суждении субъект всегда нераспределён), так и в меньшей посылке (в общеутвердительном суждении предикат, как правило, нераспределён). Если средний термин нераспределён в обеих посылках, то затруднительно сказать что-то определённое о соотношении крайних терминов.

3. Термин, не распределённый в посылке, не может быть распределён в выводе.

Пример:

Все стоматологи – врачи

Некоторые люди – стоматологи

Все люди – врачи

Здесь очевидная ошибка получается вследствие того, что термин «люди» в посылке берётся лишь в части объёма – говорится о «некоторых людях», а в заключении мы говорим обо всём его объёме – «все люди». Правильным был бы вывод: «Некоторые люди являются врачами».

Правила посылок:

1. Из двух отрицательных посылок вывод не следует.

Пример:

Ни один велосипед (M) не является мотоциклом (P).

Ни один самокат (S) не является велосипедом (M).

?

В первой посылке отрицается связь большего термина (P) со средним термином (M); во второй отрицается связь меньшего термина (S) со средним термином (M). Получается, что средний термин не может обеспечить связь крайних терминов. Мы не можем ничего сказать о соотношении S и P. Если изобразить отношения между терминами в данном силлогизме, то схема будет такая:

Вывод оказывается невозможным.

2. Из двух частных посылок вывод не следует.

Если в силлогизме две частные посылки, то возможны следующие сочетания: обе посылки – частноутвердительные суждения, обе посылки – частноотрицательные суждения, одна из посылок – частноутвердительное суждение, другая – частноотрицательное суждение.

Пример:

Некоторые стулья (M) –деревянные (P).

Некоторые предметы мебели (S) –стулья (M).

?

В данном силлогизме средний термин нераспределён ни в одной из посылок, т.к. в первой посылке – он субъект частноутвердительного суждения, а во второй – предикат частноутвердительного суждения.

Если обе посылке являются частноотрицательными суждениями, то вывода из них не следует согласно правилу 1 (правила посылок).

Если одна из посылок – частноутвердительное суждение, другая – частноотрицательное суждение, то здесь возможны два варианта:

1) Некоторые M есть P.

Некоторые S не есть M.

?

2) Некоторые M не есть P.

Некоторые S есть M.

?

В первом случае больший термин P не распределён как предикат утвердительного суждения, но в выводе он должен быть распределён как предикат отрицательного суждения. Это нарушает правило 3 (правила терминов). Во втором случае средний термин M не распределён ни в одной из посылок, что нарушает правило 2 (правила терминов).

3. Если одна из посылок частное суждение, то и вывод должен быть частным.

Пример:

Все львы – млекопитающие.

Некоторые животные – львы.

Некоторые животные – млекопитающие.

Попытка при частной посылке сделать общий вывод приводит к нарушению правила 3 (правила терминов). Меньший термин (S) нераспределённый в посылке будет распределён в заключение.

Пример:

Все киты – млекопитающие.

Некоторые животные – киты.

Все животные – млекопитающие.

В данном силлогизме меньший термин – «животные» нераспределён в посылке, но распределён в заключение.

4. Если одна из посылок отрицательное суждение, то и вывод должен быть отрицательным.

Пример:

Все сосны – хвойные деревья.

Это дерево не является хвойным.

Это дерево не является сосной.

Отрицательная посылка означает, что либо M лежит вне P, либо S лежит вне M. В обоих случаях вывод может быть только один: S лежит вне P.

Специальные правила для I фигуры:

1. Большая посылка должна быть общей.

2. Меньшая посылка должна быть утвердительной.

Специальные правила для II фигуры:

1. Большая посылка должна быть общей.

2. Одна из посылок должна быть отрицательным суждением.

Специальные правила для III фигуры:

1. Меньшая посылка должна быть утвердительной.

2. Заключение должно быть частным суждением.

Специальные правила для IV фигуры:

1. Если большая посылка – утвердительное суждение, то меньшая посылка должна быть общим суждением.

2. Если одна из посылок – отрицательное суждение, то большая посылка должна быть общей.

3. Вывод всегда частное суждение.

Правильные модусы: I фигура – AAA, EAE, AII, EIO; II фигура – EAE, AEE, EIO, AOO; III фигура – AAI, IAI, AII, EAO, OAO, EIO; IV фигура – AAI, AEE, IAI, EAO, EIO.

На основе простого категорического силлогизма могут быть построены сокращенные (энтимемы), сложные (полисиллогизмы) и сложносокращенные силлогизмы (сориты).

Энтимема – сокращенный категорический силлогизм, в котором пропущена одна из посылок или отсутствует заключение.

Например, «Юпитер, ты сердишься, значит ты не прав».

Для того чтобы восстановить эту энтимему, необходимо выяснить какой из элементов пропущен (одна из посылок или заключение). Необходимо помнить, что после слов «следовательно», «поэтому», «значит» следует заключение, после «так как» – посылка. Если суждения в энтимеме связаны союзами «но», «а», «и», то пропущено заключение.

В нашем примере пропущена одна из посылок – большая, так как имеющаяся посылка является меньшей, ибо содержит субъект заключения. Если восстановить недостающую посылку, то получится следующий силлогизм:

Тот, кто сердится, тот не прав.

Юпитер, ты сердишься.

Юпитер, ты не прав.

Или, например, «Все киты – млекопитающие, а кашалоты – киты».

В этой энтимеме суждения связаны союзом «а», значит пропущено заключение. Если восстановить заключение, то получится следующий силлогизм:

Все киты – млекопитающие.

Все кашалоты – киты.

Все кашалоты – млекопитающие.

Или, например, «Все профессиональные музыканты знают нотную грамоту, поэтому Оленев знает нотную грамоту».

В данной энтимеме пропущена меньшая посылка, так как имеющаяся посылка: «Все профессиональные музыканты знают нотную грамоту» является большей, ибо содержит предикат заключения. Если восстановить недостающую посылку, то получится следующий силлогизм:

Все профессиональные музыканты знают нотную грамоту

Оленев – профессиональный музыкант

Оленев знает нотную грамоту

Полисиллогизм – сложный силлогизм, состоящий из двух и более простых категорических силлогизмов, связанных между собой таким образом, что заключение каждого предыдущего силлогизма становится большей (в прогрессивном полисиллогизме) или меньшей (в регрессивном полисиллогизме) посылкой другого силлогизма.

Общая схема прогрессивного полисиллогизма:

Все A суть B.

Все C суть A.

Все C суть B.

Все D суть C.

Все D суть B.

Пример:

Спорт (A) укрепляет здоровье (B)

Плавание (C) – спорт (A)

Плавание (C) укрепляет здоровье (B)

Синхронное плавание (D) – плавание (C)

Синхронное плавание (D) укрепляет здоровье (B)

Общая схема регрессивного полисиллогизма:

Все A суть B.

Все B суть C.

Все A суть C.

Все C суть D.

Все A суть D.

Пример:

Берёзы (A) – деревья (B)

Деревья (B) – растения (C)

Берёзы (A) – растения (C)

Растения (C) – организмы (D)

Берёзы (A) – организмы (D)

Сорит – сокращённый полисиллогизм, в котором пропущены заключение предшествующего силлогизма и одна из посылок последующего силлогизма. Так же, как и полисиллогизм, сорит имеет две схемы.

Общая схема прогрессивного сорита:

Все A суть B.

Все C суть A.

Все D суть C.

Все D суть B.

Пример:

Всё, что укрепляет здоровье (A) – полезно (B)

Физкультура (C) укрепляет здоровье (A)

Прыжки (D) – вид физкультуры (C)

Прыжки (D) укрепляют здоровье (A)

Общая схема регрессивного сорита:

Все A суть B.

Все B суть C.

Все C суть D.

Все A суть D.

Пример:

Все ромашки (A) – цветы (B)

Все цветы (B) – растения (C)

Все растения (C) дышат (D)

Все ромашки (A) дышат (D)

Эпихейрема – сокращённый и одновременно сложный силлогизм, посылки которого представляют собой энтимемы.

Пример:

Ни одна птица не примат, так как ни одна птица не млекопитающее.

Данные особи – птицы, так как они имеют перьевой покров.

Данные особи не приматы

Восстановив пропущенные посылки, мы получаем два простых категорических силлогизма модуса AEE II фигуры и модуса AAA I фигуры:

Все приматы – млекопитающие

Ни одна птица не млекопитающее

Ни одна птица не примат

Все имеющие перьевой покров являются птицами

Данные особи имеют перьевой покров

Данные особи – птицы

Кроме простого категорического силлогизма выделяют силлогизмы со сложными суждениями. К ним относятся условно-категорический силлогизм, разделительно-категорический силлогизм и условно-разделительный силлогизм.

В условно-категорическом силлогизме первая посылка является условным суждением, вторая посылка и вывод – простыми категорическими суждениями.

Условно-категорический силлогизм имеет два правильных модуса:

1) утверждающий (modus ponens) – категорическая посылка утверждает истинность основания, заключение утверждает истинность следствия. Его схема в символической записи:

A→B, A ;

B

Пример:

Если человек болен гриппом (A), то у него высокая температура (B)

Данный человек болен гриппом (A)

У данного человека высокая температура (B)

2) отрицающий (modus tollens) – категорическая посылка отрицает истинность следствия, заключение отрицает истинность основания. Его схема в символической записи:

A→B, ~B .

~A

Пример:

Если будет кворум (A), то собрание состоится (B)

Собрание не состоялось (~B)

Кворума не было (~A)

Два других модуса: 3) от отрицания истинности основания к отрицанию истинности следствия и 4) от утверждения истинности следствия к утверждению истинности основания – достоверных выводов не дают. Их схемы в символической записи:

A→B, ~A; A→B, B .

~B A

Например:

Если идет дождь (А), то на улице мокро (В)

На улице мокро (В)

Дождь идет (А)

В данном случае причиной того, что «на улице мокро», вовсе не обязательно будет дождь.

Или, например:

Если у человека высокая температура (A), то он болен (B)

У данного человека нет высокой температуры (~A)

Данный человек не болен (~B)

В этом силлогизме вывод тоже носит вероятностный характер, так как есть болезни, которые не сопровождаются повышением температуры.

Если первая посылка является эквивалентным суждением, то есть если следствие (В) вызывается данной и только данной причиной (А), то достоверные выводы получаются по всем четырём модусам.

Анализируя условное суждение, необходимо правильно выявить какая часть условного суждения является основанием, а какая – следствием.

Разделительно-категорический силлогизм есть умозаключение, в котором первая посылка является разделительным суждением, а вторая посылка и вывод – простыми категорическими суждениями.

Разделительно-категорический силлогизм имеет два правильных модуса: