Комбинационные элементы. Сумматоры и АЛУ. Номенклатура и характеристики ТТЛ серий

Сумматоры

Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов. Например, если один входной код - 7 (0111), а второй - 5 (0101), то суммарный код на выходе будет 12 (1100). Сумма двух двоичных чисел с числом разрядов N может иметь число разрядов (N + 1). Например, при суммировании чисел 13 (1101) и 6 (0110) получается число 19 (10011). Поэтому количество выходов сумматора на единицу больше количества разрядов входных кодов. Этот дополнительный (старший) разряд называется выходом переноса.

На схемах сумматоры обозначаются буквами SM. В отечественных сериях код, обозначающий микросхему сумматора, - ИМ.

Сумматоры бывают одноразрядные (для суммирования двух одноразрядных чисел), 2-х разрядные (суммируют 2-х разрядные числа) и 4-х разрядные (суммируют 4-х разрядные числа). Чаще всего применяют именно 4-разрядные сумматоры. На рис. 6.1 показаны для примера 2-разрядный и 4-разрядный сумматоры. Микросхема ИМ6 отличается от ИМ3 только повышенным быстродействием и номерами используемых выводов микросхемы, функция же выполняется та же самая.

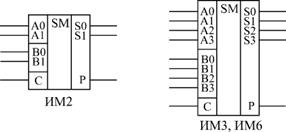
Рис. 6.1. Примеры микросхем сумматоров

Помимо выходных разрядов суммы и выхода переноса, сумматоры имеют вход расширения (другое название - вход переноса) С для объединения нескольких сумматоров с целью увеличения разрядности. Если на этот вход приходит единица, то выходная сумма увеличивается на единицу, если же приходит нуль, то выходная сумма не увеличивается. Если используется одна микросхема сумматора, то на ее вход расширения С необходимо подать нуль.

Для примера в табл. 6.1 приведена полная таблица истинности 2-разрядного сумматора ИМ2. Как видно из таблицы, выходной 3-разрядный код (Р, S1, S0) равен сумме входных 2-разрядных кодов (А1, А0) и (В1, В0), а также сигнала С. Нулевые разряды - младшие, первые разряды - старшие. Полная таблица истинности 4-разрядного сумматора будет чрезмерно большой, поэтому она не приводится. Но суть работы остается точно такой же, как и в случае 2-разрядного сумматора.

Сумматоры могут использоваться также для суммирования чисел в отрицательной логике (когда логической единице соответствует электрический нуль, и наоборот, логическому нулю соответствует электрическая единица). Но в этом случае входной сигнал переноса С также становится инверсным, поэтому при использовании одной микросхемы сумматора на вход С надо подать электрическую единицу (высокий уровень напряжения). Инверсным становится и выходной сигнал переноса Р, низкий уровень напряжения на нем (электрический нуль) соответствует наличию переноса. То есть получается, что сумматор абсолютно одинаково работает как с положительной, так и с отрицательной логикой.

Таблица 6.1. Таблица истинности микросхемы 2-разрядного сумматора ИМ2
Входы	Выходы
	C=0	C=1
A1	A0	B1	B0	P	S1	S0	P	S1	S0

Рассмотрим пример. Пусть нам надо сложить два числа 5 и 7 в отрицательной логике. Числу 5 в положительной логике соответствует двоичный код 0101, а в отрицательной - код 1010. Числу 7 в положительной логике соответствует двоичный код 0111, а в отрицательной - код 1000. При подаче на вход сумматора кодов 1010 (десятичное число 10 в положительной логике) и 1000 (десятичное число 8 в положительной логике) получаем сумму 10 + 8 = 18, то есть код 10010 в положительной логике. С учетом входного сигнала переноса С=1 (отсутствие входного переноса в отрицательной логике) выходной код сумматора получится на единицу больше: 18 + 1 = 19, то есть 10011. При отрицательной логике это будет соответствовать числу 01100, то есть 12 при отсутствии выходного переноса. В результате получили 5+7=12.

Сумматор может вычислять не только сумму, но и разность входных кодов, то есть работать вычитателем. Для этого вычитаемое число надо просто поразрядно проинвертировать, а на вход переноса С подать единичный сигнал (рис. 6.2).

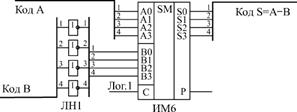
Рис. 6.2. 4-х разрядный вычитатель на сумматоре ИМ6 и инверторах ЛН1

Например, пусть нам надо вычислить разность между числом 11 (1011) и числом 5 (0101). Инвертируем поразрядно число 5 и получаем 1010, то есть десятичное 10. Сумматор при суммировании 11 и 10 даст 21, то есть двоичное число 10101. Если сигнал С равен 1, то результат будет 10110. Отбрасываем старший разряд (выходной сигнал Р) и получаем разность 0110, то есть 6.

Еще пример. Пусть надо вычислить разность между числом 12 (1100) и числом 9 (1001). Инвертируем поразрядно 9, получаем 0110, то есть десятичное 6. Находим сумму 12 и 6, получаем 18, а с учетом С = 1 получаем 19, то есть двоичное 10011. В четырех младших разрядах имеем 0011, то есть десятичное 3.

Каскадировать сумматоры для увеличения разрядности очень просто. Надо сигнал с выхода переноса сумматора, обрабатывающего младшие разряды, подать на вход переноса сумматора, обрабатывающего старшие разряды (рис. 6.3). При объединении трех 4-разрядных сумматоров получается 12-разрядный сумматор, имеющий дополнительный 13-й разряд (выход переноса Р).

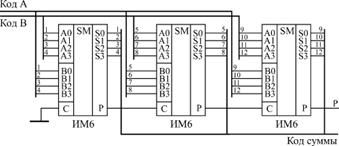
Рис. 6.3. Каскадирование сумматоров ИМ6 для увеличения разрядности

Неопределенные состояния на выходах сумматора могут возникать при любом изменении любого из входных кодов (рис. 6.4). Выходной код суммы может принимать в течение короткого времени значения, никак не связанные с входными кодами, а на выходе переноса могут появляться короткие паразитные импульсы. Это связано прежде всего с неодновременным изменением разрядов входных кодов. Чтобы избежать влияния этих неопределенных состояний на дальнейшую схему, необходимо предусматривать синхронизацию или стробирование выходных сигналов. Но для этого надо располагать информацией о моментах изменения входных кодов, которая имеется далеко не всегда.

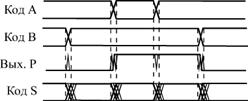
Рис. 6.4. Неопределенные состояния на выходах сумматора при изменении входных кодов

Задержки сумматора ИМ6 от входов до выходов суммы примерно вдвое превышает задержку логического элемента, а от входов до выхода переноса - примерно в полтора раза. Задержки сумматора ИМ3 больше задержек ИМ6 почти вдвое. Поэтому в схемах, где важно быстродействие, лучше использовать ИМ6. Особенно это существенно при каскадировании для увеличения разрядности, так как там задержки отдельных микросхем суммируются. Точные величины задержек надо смотреть в справочниках.

Арифметическо-логическое устройство – схема комбинационного типа, не требующая для своей работы каких-либо привязанных ко времени тактовых сигналов. Результат операции появляется на выходе АЛУ спустя задержку, равную сумме задержек логических элементов, образующих самую длинную цепь внутри АЛУ. Из-за последовательного прохождения переноса через все разряды АЛУ, длина самой длинной цепи, а следовательно, и общая задержка АЛУ растет пропорционально его разрядности. Грубо говоря, задержка 32-разрядного АЛУ будет в 32 раза больше, чем задержка одноразрядного АЛУ. Использование специальных схем ускоренного переноса позволяет в несколько раз уменьшить задержку многоразрядных АЛУ.

В общем случае многофункциональное АЛУ включает операционную часть (ОУ) и устройство управления (УУ), которое осуществляет вторичную дешифрацию кода команды и определяет выполняемую в АЛУ операцию.

.

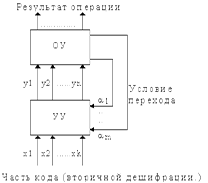
Рисунок 4.2. Структура АЛУ

Набор выполняемых в АЛУ операций должен обладать функциональной полнотой. Чтобы обеспечить функциональную полноту достаточно четырех операций :

• обращение к памяти для записи/чтения данных;
• инкремент/декремент;
• сравнение (реализует возможность условного перехода);
• останов работы устройства.

В первых процессорах количество операций ограничивалось шестнадцатью, теперь достигает нескольких сотен.

Количество выполняемых операций является важной характеристикой АЛУ.

Классификация АЛУ

АЛУ можно классифицировать по ряду признаков, приведенных ниже.

Классификация по способу представления данных:

• с фиксированной запятой;
• с плавающей запятой.

2. Классификация по способу действия над операндами:

·последовательные АЛУ, где каждая операция выполняется последовательно над каждым разрядом;

·параллельные АЛУ, операция выполняется над всеми разрядами данных одновременно;

·последовательно - параллельные АЛУ, где слово данных делится на слоги, обработка данных ведется параллельно над разрядами слога и последовательно над слогами.

3. Классификация по использованию систем счисления:

• двоичная;

· двоично- десятичная;

· восьмеричная;

· шестнадцатеричная;

• и т.д.

4. Классификация по характеру использования элементов и узлов:

• блочные- для выполнения отдельных арифметических операций в структуру АЛУ вводят специальные блоки, что позволяет процесс обработки информации вести параллельно;
• конвейерные- в конвейерных АЛУ операция разбивается на последовательность микроопераций, выполняемых за одинаковые промежутки времени (такты) на разных ступенях конвейера, что позволяет выполнять операцию над потоком операндов каждый такт;
• многофункциональные- это универсальные АЛУ, выполняющие множество операций в одном устройстве. В таких АЛУ требуется настройка на выполнение данной операции при помощи кода операции.

5.Классификация по временным характеристикам.

По временным характеристикам АЛУ делятся на:

• синхронные- в синхронных АЛУ каждая операция выполняется за один такт.
• асинхронные- не тактируемые АЛУ, обеспечивающие высокое быстродействие, так как выполняются на комбинационных схемах.

6.Классификация по структуре устройства управления: