Построение графа переходов абстрактного автомата и таблицы переходов-выходов
ВВЕДЕНИЕ
Согласно заданию необходимо провести синтез автомата модели Мили. На вход автомата поступает 16 различных входных последовательностей длины 4, составленных из букв алфавита 0, 1. На выходе вырабатывается 16 выходных последовательностей, составленных из букв того же алфавита. Для задания работы автомата используется оператор соответствия, представляющий собой таблицу, в которой каждому входному набору сигналов ставится в соответствие выходной набор. Заполнение оператора соответствия ведется на основе заданного числа W по определенному правилу.
После заполнения оператора соответствия необходимо привести его к автоматному виду с помощью введения пустых символов во входной и выходной алфавит (α и β соответственно). Затем строится граф переходов автомата Мили. По построенному графу строится совмещенная таблица переходов-выходов. Минимизация числа состояний выполняется в два этапа. На первом этапе необходимо найти и объединить в одно все состояния, имеющие одинаковые выходные символы и при переходе вырабатывающие одинаковые состояния. Второй этап минимизации проводится с помощью треугольной таблицы.
После минимизации необходимо провести структурный синтез автомата. На данном этапе осуществляется
1) выбор метода устранения критических состязаний (гонок) элементов памяти в автомате;
2) кодирование состояний автомата, входных и выходных символов;
3) составление таблицы функций возбуждения для JK-триггера;
4) формирование логических выражений для функций возбуждения и их минимизация с помощью карт Вейча;
5) построение кодированной таблицы выходов;
6) формирование логических выражений для выходов и их минимизация с помощью карт Вейча.
На основе минимизированных выражений строится схема электрическая функциональная в базисе "стрелка Пирса". Проверка работоспособности схемы осуществляется с помощью симулятора MAX+PLUS.
АБСТРАКТНЫЙ СИНТЕЗ КОНЕЧНОГО АВТОМАТА
ФОРМИРОВАНИЕ ОПЕРАТОРА СООТВЕТСТВИЯ
Формирование оператора соответствия ведется следующим образом:
I. заданное число W нормализуется, и мантисса переводится в двоичную систему счисления; переведенное 16-разрядное число записывается в столбец W1;
По заданию W = 0.104041. Осуществим его перевод в двоичную систему счисления. Для этого исходная дробь умножается на основание системы счисления, в которую переводится; в полученном произведении целая часть преобразуется в соответствии с таблицей в цифру нужной системы счисления и отбрасывается - она является старшей цифрой получаемой дроби; оставшаяся дробная часть вновь умножается на нужное основание системы счисления с последующей обработкой полученного произведения в соответствии с шагами. Произведем эти действия.
1) 0.104041∙2 = 0.208082
2) 0.208082∙2 = 0.416164
3) 0.416164∙2 = 0.832328
4) 0.832328∙2 = 1.664656
5) 0.664656∙2 = 1.329312
6) 0.329312∙2 = 0.658624
7) 0.658624∙2 = 1.317248
8) 0.317248∙2 = 0.634496
9) 0.634496∙2 = 1.268992
10) 0.268992∙2 = 0.537984
11) 0.537984∙2 = 1.075968
12) 0.075968∙2 = 0.151936
13) 0.151936∙2 = 0.303872
14) 0.303872∙2 = 0.607744
15) 0.607744∙2 = 1.215488
16) 0.215488∙2 = 0.430976
Таблица 1.1.1 – Перевод в двоичную систему счисления числа W
II. нормализованная мантисса числа W возводится в квадрат, нормализуется и переводится в двоичную систему, переведенное 16-разрядное число записывается в столбец W2;
W2 = (0.104041)2 = 0.0108245. В результате нормализации получаем 0.108245
1) 0.108245∙2 = 0.216490
2) 0.216490∙2 = 0.432980
3) 0.432980∙2 = 0.865960
4) 0.865960∙2 = 1.731920
5) 0.731920∙2 = 1.463840
6) 0.463840∙2 = 0.927680
7) 0.927680∙2 = 1.855360
8) 0.855360∙2 = 1.710720
9) 0.710720∙2 = 1.421440
10) 0.421440∙2 = 0.842880
11) 0.842880∙2 = 1.685760
12) 0.685760∙2 = 1.371520
13) 0.371520∙2 = 0.743040
14) 0.743040∙2 = 1.486080
15) 0.486080∙2 = 0.972160
16) 0.972160∙2 = 1.944320
Таблица 1.1.2 – Перевод в двоичную систему счисления числа W2
III. нормализованная мантисса числа W возводится в куб, нормализуется и переводится в двоичную систему, переведенное 16-разрядное число записывается в столбец W3;
W3 = (0.104041)3 = 0.001126194. В результате нормализации получаем 0.1126194
1) 0.1126194∙2 = 0.225238
2) 0.225238∙2 = 0.450476
3) 0.450476∙2 = 0.900952
4) 0.900952∙2 = 1.801904
5) 0.801904∙2 = 1.603808
6) 0.603808∙2 = 1.207616
7) 0.207616∙2 = 0.415232
8) 0.415232∙2 = 0.830464
9) 0.830464∙2 = 1.660928
10) 0.660928∙2 = 1.321856
11) 0.321856∙2 = 0.643712
12) 0.643712∙2 = 1.287424
13) 0.287424∙2 = 0.574848
14) 0.574848∙2 = 1.149696
15) 0.149696∙2 = 0.299392
16) 0.299392∙2 = 0.598784
Таблица 1.1.3 – Перевод в двоичную систему счисления числа W3
IV. нормализованная мантисса числа W возводится в четвертую степень, нормализуется и переводится в двоичную систему, переведенное 16-разрядное число записывается в столбец W4;
W4 = (0.104041)4 = 0.00011717. В результате нормализации получаем 0.11717
1) 0.11717∙2 = 0.23434
2) 0.46868∙2 = 0.93736
3) 0.93736∙2 = 1.87472
4) 0.87472∙2 = 1.74944
5) 0.74944∙2 = 1.49888
6) 0.49888∙2 = 0.99776
7) 0.99776∙2 = 1.99552
8) 0.99552∙2 = 1.99104
9) 0.99104∙2 = 1.98208
10) 0.98208∙2 = 1.96416
11) 0.96416∙2 = 1.92832
12) 0.92832∙2 = 1.85664
13) 0.85664∙2 = 1.71328
14) 0.71328∙2 = 1.42656
15) 0.42656∙2 = 0.85312
16) 0.85312∙2 = 1.70624
Таблица 1.1.4 – Перевод в двоичную систему счисления числа W3
Полученный в результате вычислений оператор сооответствия представлени в таблице 1.1.5.
Таблица 1.1.5 – Оператор соответствия
| Входные сигналы | Выходные сигналы | |||||||
| Z1 | Z2 | Z3 | Z4 | W1 | W2 | W3 | W4 | |
ПРИВЕДЕНИЕ ОПЕРАТОРА СООТВЕТСТВИЯ К АВТОМАТНОМУ ВИДУ
Приведем оператор соответствия к автоматному виду в соответствии со следующими правилами:
1) длины входной последовательности и соответствующей ей выходной должны быть одинаковыми
2) на одинаковые начальные участки входной последовательности автомат должен отвечать формированием одинаковых начальных участков выходных последовательностей
Приведение оператора соответствия к автоматному виду осуществляется путем использования пустых символов α и β.
Результат приведения представлен в таблице 1.2.1.
Таблица 1.2.1 – Автоматный оператор соответствия
| Входные сигналы | Выходные сигналы | |||||||||||||
| Z1 | Z2 | Z3 | Z4 | W1 | W2 | W3 | W4 | |||||||
| α | α | β | β | |||||||||||
| α | α | β | β | |||||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β | |||||||||
| α | α | β | β | |||||||||||
| α | α | β | β | |||||||||||
| α | α | α | β | β | β | |||||||||
| α | α | α | β | β | β |
ПОСТРОЕНИЕ ГРАФА ПЕРЕХОДОВ АБСТРАКТНОГО АВТОМАТА И ТАБЛИЦЫ ПЕРЕХОДОВ-ВЫХОДОВ
Граф переходов автомата Мили строится на основе таблицы 1.2.1. При этом предполагается, что последний символ каждого входного слова должен переводит автомат в начальное состояние.
В момент времени t = 0 автомат находится в состоянии а0. При подаче в последующие моменты времени каждого входного сигнала z(t) автомат вырабатывает выходной сигнал w(t) и переходит в новое состояние. Порядок нумерации состояний, отличных от начального, для абстрактного автомата безразличен.
Рассмотрим для примера первую строчку в таблице 1.2.1. Под воздействием нуля автомат переходит из а0 в а1 и вырабатывает сигнал β. Под воздействием второго нуля автомат из а1 переходит в а3 и вырабатывает сигнал β. Под воздействием третьего нуля автомат из а3 переходит в а7 и вырабатывает сигнал 0. Под воздействием четвертого нуля автомат из а7 переходит в а15 и вырабатывает сигнал 0. Далее под воздействием первого α автомат из а15 переходит в а31 и вырабатывает сигнал 0. Под воздействием второго α автомат из а31 переходит снова в а0 и вырабатывает сигнал 0. Рассуждая аналогичным образом можно построить остальные ветки графа.
Граф переходов заданного автомата представлен на рисунке 1.3.1.
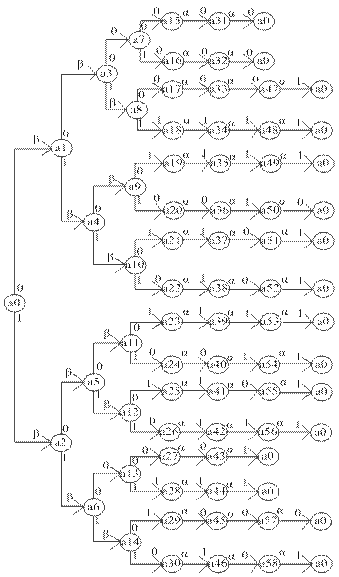
Рисунок 1.3.1 – Граф переходов автомата Мили
На основе полученного графа построим таблицу переходов-выходов.
Таблица 1.3.1 – Таблица переходов-выходов
| α | |||
| a0 | a1/β | a2/ β | – |
| a1 | a3/β | a4/β | – |
| a2 | a5/β | a6/β | – |
| a3 | a7/0 | a8/β | – |
| a4 | a9/β | a10/β | – |
| a5 | a11/β | a12/β | – |
| a6 | a13/0 | a14/β | – |
| a7 | a15/0 | a16/0 | – |
| a8 | a17/0 | a18/1 | – |
| a9 | a19/1 | a20/0 | – |
| a10 | a21/1 | a22/0 | – |
| a11 | a23/1 | a24/0 | – |
| a12 | a25/1 | a26/0 | – |
| Таблица 1.3.1 – Продолжение | |||
| a13 | a27/0 | a282/1 | – |
| a14 | a29/1 | a30/0 | – |
| a15 | – | – | a31/0 |
| a16 | – | – | a32/0 |
| a17 | – | – | a33/0 |
| a18 | – | – | a34/1 |
| a19 | – | – | a35/1 |
| a20 | – | – | a36/0 |
| a21 | – | – | a37/1 |
| a22 | – | – | a38/1 |
| a23 | – | – | a39/1 |
| a24 | – | – | a40/0 |
| a25 | – | – | a41/1 |
| a26 | – | – | a42/1 |
| a27 | – | – | a43/0 |
| a28 | – | – | a44/1 |
| a29 | – | – | a45/0 |
| a30 | – | – | a46/1 |
| a31 | – | – | a0/0 |
| a32 | – | – | a0/0 |
| a33 | – | – | a47/0 |
| a34 | – | – | a48/1 |
| a35 | – | – | a49/1 |
| a36 | – | – | a50/1 |
| a37 | – | – | a51/0 |
| a38 | – | – | a52/0 |
| a39 | – | – | a53/1 |
| a40 | – | – | a54/1 |
| a41 | – | – | a55/0 |
| a42 | – | – | a56/1 |
| a43 | – | – | a0/1 |
| a44 | – | – | a0/1 |
| a45 | – | – | a57/0 |
| a46 | – | – | a58/0 |
| a47 | – | – | a0/1 |
| a48 | – | – | a0/1 |
| a49 | – | – | a0/1 |
| a50 | – | – | a0/0 |
| a51 | – | – | a0/1 |
| a52 | – | – | a0/1 |
| a53 | – | – | a0/1 |
| a54 | – | – | a0/1 |
| a55 | – | – | a0/1 |
| a56 | – | – | a0/1 |
| a57 | – | – | a0/0 |
| a58 | – | – | a0/1 |
