Семантика логики высказываний

Перечисление исходных знаков (символов) и правил образования формул составляет синтаксис языка. Пока мы не придадим нашим знакам никаких значений, мы имеем лишь некоторую схему языка. Операция приписывания определенных значений выражениям языка называется интерпретацией. При этом логические константы получают единую и постоянную для данного языка интерпретацию, а пропозициональные переменные в составе формул, – могут получить различные интерпретации от случая к случаю. Существование этой интерпретации определяет семантику языка. Интерпретации подлежат лишь значимые выражения языка. Наряду с пропозициональными переменными к ним принадлежат теперь и формулы. Интерпретацию можно разбить на два этапа. На первом этапе указываются лишь типы возможных значений для значащих выражений языка.

Этапы интерпретации:

1. Пропозициональным знакам в качестве предметных значений приписываются объекты из множества истинностных значений – И (истина), Л (ложь). При этом каждому пропозициональному знаку в каждом случае интерпретации приписывается лишь одно из указанных значений. Естественно, подразумевается, что эти объекты (И, Л) являются истинностными значениями каких-то высказываний, от смысловых структур которых мы отвлекаемся в языке логики высказываний.

2. Формулам приписываются значения того же типа (И, Л) по следующим правилам:

♦ Формула вида А & В имеет значение И, если и только если значение А есть И и значение В есть И. В противном случае – если значение А, или значение В, или значения обоих вместе есть Л – формула этого вида имеет значение Л.

♦ Формула вида А 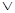В имеет значение И если и только если – какая-нибудь из ее составляющих – А или В – имеет это значение.

♦ Значение А 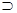есть И если и только если имеет место какой-нибудь из случаев (или оба): значение А = Л или значение В = И.

♦ Значение формулы вида 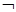А есть И если и только если значение А = Л.

Из этих правил видно, что конъюнкция (&) в применении к двум высказываниям А и В указывает на наличие в действительности ситуаций, описываемых в высказываниях А и В. Они соответствует союзу «и» естественного языка при некоторых типичных его употреблениях.

Дизъюнкция ( 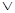) в применении к таким же высказываниям указывает на наличие какой-нибудь из этих ситуаций, а, возможно, и обеих. Она представляет собой аналог естественноязыкового слова «или», когда оно употребляется в разделительном смысле.

Отрицание высказывания А ( 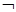А)указывает на отсутствие ситуации А.

Импликация ( 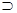).Эта связка соответствует союзу «если…, то…» естественного языка, используемого для выражения некоторой связи между явлениями действительности. Например: «Если по проводнику течет ток, то проводник нагревается» или «Если число оканчивается на 0 или на 5, то оно делится на 5» и т.д. Логическая же связка « 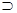» является результатом определенного упрощения смысла этого союза. В результате этого упрощения истинными являются, например, такие высказывания, как: «Если Эйфелева башня находится в Англии, то Париж столица Англии» или «Если Эйфелева башня находится в Париже, то Новосибирск находится в Сибири». Первое их этих высказываний истинно в силу ложности первого члена импликации, который называется антецедентом импликации. Второе истинно в силу истинности второго члена импликации, называемого консеквентом импликации. Несмотря на такое упрощение, и даже в силу его, эта связка оказывается весьма полезной в составе описываемого языка при использовании его как инструментов для анализа определенных логических процедур и отношений в рамках естественного языка.

В результате указанной интерпретации логических связок каждая формула приобретает некоторый смысл. Они представляют собой логические формы возможных высказываний. Назовем такие формулы полуинтерпретированными. Полная интерпретация той или иной формулы получается в результате приписывания истинностных значений пропозициональным переменным. Полностью интерпретированная формула – это некоторое высказывание нашего языка. 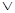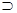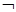Такая интерпретация формул интересует логику лишь при решении некоторых конкретных задач, например, при вычислении истинностных значений сложных высказываний вида (p q) p при заданных значениях его составляющих: значение р – Л (ложь), q – И (истина). 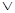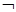Для вычисления всего выражения надо вычислить значения его составляющих (p q) и p.