Тема 10. Теория дедуктивных рассуждений

Изучив материалы темы, Вы сможете:

- уяснить смысл и значение теории дедуктивных рассуждений;

- понять, что такое система натурального вывода;

- объяснить разницу между системой естественного вывода логики высказываний и системой естественного вывода логики предикатов;

- дать определение кратной импликации;

- знать правила логического следования, правила построения прямого доказательства, правила построения косвенного доказательства и кванторные правила вывода;

Исследование рассуждений, их видов и способов осуществления входит в число основных задач логики. В общем случае под рассуждением понимают процедуру последовательного пошагового перехода от одних высказываний, принятых в качестве исходных, к другим высказываниям. Каждый шаг этого процесса осуществляется на основе некоторого правила, называемого правилом вывода. Последнее высказывание, полученное в данном процессе, называется заключением рассуждения.

Дедуктивными являются лишь те рассуждения, в которых между высказываниями, принятыми в качестве исходных, и заключением сохраняется отношение логического следования.

Теория дедуктивных рассуждений отвечает на вопрос, как строятся рассуждения дедуктивного типа.

Процедуры дедукции, как теоретического метода исследования имеют большое значение при построении научного знания. В зависимости от степени прояснённости дедуктивных связей между отдельными утверждениями теорий различают несколько их типов. К первому типу относятся содержательные теории. В их составе дедукция если и используется, то лишь для связи некоторых отдельных положений теории. При этом исходные утверждения в рассуждениях представляют собой некоторые допущения, называемые посылками. Посылки не обязаны быть истинными, а потому любое предложение, которое дедуцируется с их использованием, считается не истинным, а условно истинным: заключительное предложение истинно при условии, что посылки являются истинными. Примерами логических содержательных теорий являются логики высказываний и предикатов.

Другой тип составляют формализованные теории. К их числу относятся теории, содержание которых взаимосвязано и дедуктивно выводится из некоторых первоначально принятых исходных утверждений. Последние называются аксиомами, а сами теории носят название аксиоматизированных теорий. Так как аксиомы представляют собой истинные высказывания о некоторой предметной области, все другие положения, дедуцируемые из них, тоже считаются истинными.

Кроме формализованных теорий, можно выделить формальные теории. В отличие от формализованных теорий, в которых специально не выделяются средства дедукции, и в силу этого многие дедуктивные шаги осуществляются на интуитивном уровне, в формальных теориях структурируется не только само знание, но и способы его получения. К формальным теориям относятся исчисление высказываний и исчисление предикатов первого порядка. Задача этих логических теорий – описание обычных процедур рассуждения, используемых в теоретической деятельности людей. Причём рассуждения, которые строятся в данных исчислениях, будут формальными рассуждениями, состоящими в выведении одних формул из других формул. Каждое такое формальное рассуждение можно трактовать как модель различных содержательных рассуждений, имеющих ту же самую логическую структуру.

Исчисление высказываний и исчисление предикатов первого порядка являются разновидностями натурального вывода. Система натурального вывода – система классической логики, которая не содержит аксиом и основывается только на правилах вывода.

Когда в обычных рассуждениях мы выводим следствия из посылок, подыскиваем посылки (гипотезы), из которых может быть выведено некоторое предложение, находим доказательства или опровержения и т. п., то во всех этих случаях наши рассуждения развёртываются в соответствии с правилами логического следования.

Как формы выражения логических законов, тождественно-истинные формулы, или логические тождества, используются для обоснования правил логического следования. С точки зрения самой процедуры их обоснования особое значение имеет способ представления формул в виде так называемых кратных импликаций.

Кратной импликацией называется формула вида

…( ) …) (*)

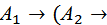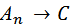Формула (*) читается так: если 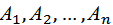, то С.

Члены кратной импликации, обозначенные в (*) посредством 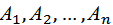называются антецедентами, а член С – консеквентом.

При n=1 имеем схему однократной (обычной) импликации

;

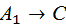при n=2 – схему двукратной импликации

;

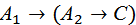при n=3 – схему трехкратной импликации

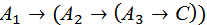
и т.д.

При n=0 считаем, что формула построенная по схеме (*) кратной импликации, совпадает с формулой С. В этом случае мы имеем дела с так называемой нулькратной, или, как ещё говорят «вырожденной» импликацией. Таким образом, нулькратная импликация содержит консеквент и не содержит антецедентов.

Любую формулу независимо от того, содержит она знак импликации в качестве главного логического знака или нет, можно рассматривать как кратную импликацию.

Важно уметь анализировать формулу с помощью схемы кратной импликации. Этот анализ может иметь различную глубину, в зависимости от того, какие части анализируемой формулы рассматриваются в качестве антецедентов 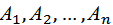и консеквента С в схеме кратной импликации.

Так, формулу

((p→q)&(q→r))→(p→r)

Можно рассматривать в качестве однократной импликации, т.е. как построенную по схеме

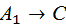
в этом случае мы в качестве 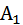берём формулу

((p→q)&(q→r)),

а в качестве С

(p→r).

Но если в качестве 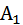взять

((p→q)&(q→r)),

в качестве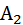

p

и в качестве С

r,

то формула

((p→q)&(q→r))→(p→r)

рассматривается теперь уже как двукратная импликация, т.е. как формула вида

.

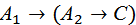Для данной формулы неосуществим более тонкий анализ по схеме кратной импликации. Но возможен ещё более грубый анализ, если всю анализируемую формулу рассматривать в качестве С, т.е. в качестве нулькратной импликации, не учитывая того, что она содержит знак импликации в качестве главного логического знака.

Между тем формулу pv(q&(~p→r)) можно рассматривать только в качестве нулькратной импликации.

При анализе формулы по схеме кратной импликации следует обращать внимание на расположение скобок. Так, каждая из приводимых ниже формул

((p→r)→p)→r,

(p→q)→(p→q)

может быть представлена в виде

,

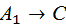но только вторая – в виде

.

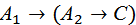Таким образом, проанализировать формулу Fпо схеме кратной импликации значит, для данной формулы подобрать схему

…( ) …)

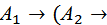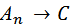с некоторым подходящим значением n и каждому 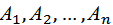, Споставить в соответствие подформулы формулы F так, что заменяя 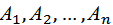, С сопоставленными им подформулами, мы снова получаем анализируемую формулу.

Анализ формулы F по схеме кратной импликации мы назовём предельным, если букве С в этой схеме ставится в соответствие подформула формулы F, не содержащая знака → в качестве главного логического знака.

В силу естественно сложившихся методов рассуждения при осуществлении процедуры обычного (неформального доказательства), особенно в математике и других точных науках, доказываемые предложения, или тезисы доказательства, приводят как правило, к форме условного предложения. Их называют теоремами. В теореме различают условие (или допущения) – часть, стоящую после слова «если» и перед словом «то», и заключение – часть стоящую после слова «то». Как явствует из способа чтения кратной импликации, формула такого вида является аналогом условного предложения; причём её антецеденты отвечают пунктам условия, а консеквент – заключению данного предложения. В свою очередь выше описанный анализ формулы по схеме кратной импликации служит аналогом процедуры выявления в доказываемом предложении условий и заключения.

С помощью табличного метода легко убедиться, что кратная импликация истинна во всех случаях, кроме того, когда каждый из её антецедентов истинен, а консеквент ложен. Кратная импликация тождественно-истинна тогда и только тогда, когда во всех строках её таблицы, где каждому антецеденту приписывается логическое значение «истинно», консеквенту приписывается то же значение.

Тождественно-истинная кратная импликация определяет некоторое правило логически корректного перехода, иначе говоря, правило логического следования, от посылок, имеющих структуру её антецедентов, к заключению, имеющему структуру её консеквента.

Логические рассуждения способствуют применению критерия практики для проверки гипотез посредством проверки выводимых из них следствий и дальнейшему превращению гипотез в теории. Правила следования играют также известную роль в подыскании гипотез и в процессах научного объяснения, поскольку возможно «применение» дедуктивных правил в обратном порядке – от заключения к посылкам.

В логике правила следования записываются в виде фигур рассуждения

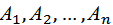
С

которые читаются так: из 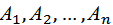следует С. Члены 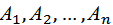называются посылками, а член С называется заключением данной фигуры. Не всякая фигура такого вида является правилом следования.

Определение правила логического следования.

Фигура

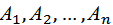
С

называется корректной фигурой, или правилом следования, если формула вида

…( ) …)

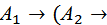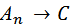есть логическое тождество.

Таким образом, для проверки корректности некоторой фигуры рассуждения, нужно образовать кратную импликацию, сделав посылки фигуры антецедентами, а заключение фигуры – консеквентом этой импликации, и выяснить, является ли полученная этим путём формула тождественно-истинной.

Применяя правила следования, мы можем из исходных формул, называемых посылками, или допущениями, получать новые формулы, логически следующие из исходных, путём построения последовательностей формул, в которых каждая формула или является посылкой, или же следует из предшествующих формул по одному из правил следования.

Такого рода последовательности формул называются формальными выводами. Они служат в логике моделями, на которых изучаются закономерности обычных логических рассуждений.

Пример. Приводимая ниже последовательность формул

1. p→(q→r) – посылка;

2. p&q – посылка;

3. p – УК (2);

4. q→r – МП (1,3);

5. q – УК (2);

6. r – МП (4,5)

есть вывод из исходных формул (посылок) 1-2 формулы 6 (заключения данного вывода), при построении которого используются правила УК и МП.

Для того чтобы придать точный смысл описательной характеристики логической структуры обычных рассуждений была создана логическая система, получившая название система естественного вывода или натуральное исчисление. В рамках данного исчисления можно строить формальные доказательства, структура которых возможно точно передаёт логическое строение обычных рассуждений.

Опишем систему естественного вывода, которую обозначим буквой N.

Основные правила системы N содержат:

Правила логического следования:

A A→B – модус поненс (МП);

B

A B –введение конъюнкции (ВК);

A&B

A&B –удаление конъюнкции (УК);

A

A&B – удаление конъюнкции (УК);

B

A – введение дизъюнкции (ВД);

AvB

B – введение дизъюнкции (ВД);

AvB

AvB A→C B→C– удаление дизъюнкции.

C

Правила построения прямого доказательства:

Прямое доказательство формулы (кратной импликации) вида

…( ) …)

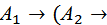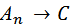строится согласно следующей процедуре.

На любом шаге построения можно написать:

1) одну из формул 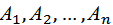в качестве допущения;

2) формулу, следующую из ранее написанных формул по одному из правил логического следования;

3) ранее доказанную формулу.

Прямое доказательство данной формулы считается построенным, если в соответствии с пп. 1)-3) получена последовательность формул оканчивающаяся формулой С.

Пример. Ниже построено доказательство формулы

(p→q)→((p&r)→(q&r))

Доказательство.

1. p→q – допущение;

2. p&r – допущение;

3. p – УК (2);

4. r – УК (2);

5. q – МП (1,3);

q&r – ВК (4,5).

Непронумерованная последняя строка означает, что доказательство закончено.

Ещё один пример. Надо доказать формулу

q→q

Доказательство.

q – допущение.

Введя в качестве допущения формулу, совпадающую с антецедентом доказываемой импликации, мы сразу же заканчиваем доказательство, потому что консеквент доказываемой импликации совпадает с её антецедентом, а, прямое доказательство заканчивается получением последовательности формул, оканчивающейся формулой, совпадающей с консеквентом доказываемой формулы.

Эту формулу мы можем использовать в процессе доказательства других формул.

Например. Следует доказать формулу

(pvq)→((p→q)→q)

Доказательство.

1. pvq – допущение;

2. p→q – допущение;

3. q→q – ранее доказанная формула (р.д.ф.);

q – УД (1, 2, 3).

Для формулировки ещё одного правила построения доказательства потребуется следующее понятие. Назовём две формулы противоречащими, если одна из них может быть получена из другой приписыванием слева знака ~.