Тема 8. Классическая логика высказываний

Изучив материалы темы, Вы сможете:

- понять, что такое логика высказываний, и какую роль она играет в анализе естественного языка;

- перевести на язык логики высказываний любое сложное суждение и построить для него таблицу истинности;

- указать основные законы логики;

- уяснить суть семантической проблемы разрешения;

- уметь использовать в качестве разрешающей процедуры построение таблиц истинности и приведение к нормальным формам формул логики высказываний;

- знать основные равносильности логики высказываний.

Логика высказываний, или исчисление высказываний – раздел математической логики, изучающий логические операции с простыми высказываниями, которые объединяются в сложные высказывания с помощью пропозициональных связок, сходных с принятыми в обычной речи союзами: «и» (в математической логике представлен символом &), «или» (v), «если…, то…» (→), «если … и только если…», «тогда и только тогда, когда» (↔), а также с отрицанием, обозначаемым частицей «не» (). Исчисление – такая система изучения тех или иных областей объективного мира, в которой предметам какой-либо определённой области ставятся в соответствие материальные знаки (цифры, буквы и др.), с которыми затем по принятым в системе точным правилам производятся операции, необходимые для решения поставленной цели.

Высказыванием в исчислении высказываний называют выражение, в отношении которого можно утверждать, что его содержание либо истинно, либо ложно.

Особенность исчисления высказываний состоит в том, что в нём не рассматривается логическая структура простых высказываний, т. е. связь между субъектом и предикатом, как это имеет место в суждении.

Алфавит логики высказываний содержит три категории знаков:

1. Пропозициональные переменные, которыми обозначают простые суждения, входящие в состав сложного –

2. Логические союзы и знак одноместной операции отрицания: ~, &, v, →, ↔, .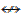

3. Скобки, которые выполняют роль знаков препинания: ( , ).

Роль структурных образований, аналогичных элементарным и сложным высказываниям, играют в этом языке формулы. Формулы – это такие конечные последовательности знаков алфавита, которые построены по определённым правилам и образуют законченные выражения логики высказываний.

Определение формулы логики высказываний:

1. Пропозициональная переменная есть формула.

2. Если А – произвольная формула, то ~А – тоже формула.

3. Если А и В – произвольные формулы, то (А&В), (АvВ), (А→В), (А↔В), (А 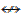В) – тоже формулы.

Заглавные латинские буквы А и В, которые употребляютсяв определении формулы, принадлежат не языку логики высказываний, а его метаязыку, то есть тому языку, на котором мы говорим о языке логики высказываний, и служит для обозначения произвольных формул, записанных на языке логики высказываний. В отличие от букв, которые являются пропозициональными переменными, их называют метапеременными, или метабуквами.

Содержащие метабуквы выражения ~А, (АvВ), (А&В), (А→В), (А↔В), (А 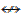В) – не формулы, а схемы формул определённого вида. Например, выражение (А&В) есть схема формул (p&q), ((p↔q)&r), ((p→q)&(sv~r)) и т.п., а выражение (АvА) – схема формул (pvp), (~qv~q), ((p→r)v(p→r)).

Каждая формула логики высказываний превращается в истинное или ложное высказывание, если все входящие в неё пропозициональные переменные заменить конкретными истинными или ложными высказываниями.

Точный смысл (семантика) логических знаков может быть разъяснён с помощью специальных таблиц, в которых зафиксировано, при каких логических значениях формул А и В формулы ~А, (А&В), (АvВ), (А→В), (А↔В), (А 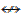В) истинны, а при каких ложны.

Таблица истинности

p	q	p&q	pvq	p 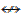q	p→q	p↔q
и и л л	и л и л	и л л л	и и и л	л и и л	и л и и	и л л и

Таблица истинности (для отрицания)

p	~p
и л	л и

Построив искусственный логический язык, постоянным которого придан точный смысл, мы можем теперь переводить на него выражения естественного языка. Перевод с обычного разговорного языка на язык логики высказываний осуществляется в результате содержательного анализа смысла предложений.

Рассмотрим в качестве примера сложное суждение: «Спортсмен подлежит дисквалификации, если он нетактично себя ведёт по отношению к сопернику или судье иесли спортсмен употребляет стимулирующие вещества». В этом сложном суждении 4 простых суждения, обозначим каждое из них пропозициональной переменной:

Спортсмен подлежит дисквалификации – p;

Он нетактично ведёт себя по отношению к сопернику – q;

Он нетактично ведёт себя по отношению к судье – r;

Спортсмен употребляет стимулирующие вещества – s.

Запишем это суждение в виде формулы:

(((qvr)&s)→p)

Осуществив перевод с естественного языка на язык логики высказываний, мы достигли того, что избавились от всей информации, которая не относится к логике, выявили логическую структуру сложного высказывания, сделали её недвусмысленной и доступной прямому наблюдению.

По каждой формуле логики высказываний всегда можно построить отвечающую ей таблицу, в которой зафиксировано, какие логические значения будет получать данная формула при различных наборах логических значений своих переменных.

Построим таблицу истинности для данной формулы, причём количество комбинаций истинностных значений определяется по формуле 2n (два в энной степени), где n – количество переменных, входящих в формулу. В нашей формуле 4 переменные, поэтому комбинаций истинностных значений будет 16:

p	q	r	s	(qvr)	((qvr)&s)	(((qvr)&s)→p)
и	и	и	и	и	и	и
и	и	и	л	и	л	и
и	и	л	л	и	л	и
и	л	л	л	л	л	и
л	л	л	л	л	л	и
л	л	л	и	л	л	и
л	л	и	и	и	и	л
л	и	и	и	и	и	л
л	и	л	и	и	и	л
и	л	и	л	и	л	и
л	л	и	л	и	л	и
и	и	л	и	и	и	и
и	л	л	и	л	л	и
л	и	и	л	и	л	и
и	л	и	и	и	и	и
л	и	л	л	и	л	и

Заключительный столбец (последний столбец в нашей таблице) содержит и значение «истина» и значение «ложь». Это значит, что наша формула является нейтральной (фактической). Существуют тождественно-истинные высказывания – это высказывание, которое при любых значениях простых суждений, входящих в его состав, имеет значение «истина». Такие высказывания называют также тавтологиями, а формулы, которые им соответствуют, тождественно-истинными формулами или законами логики. Каждая тождественно-истинная формула выражает какой-то логический закон.

Например, формула p→p является выражением закона тождества. Согласно закону тождества всякая мысль в процессе рассуждения должна оставаться тождественной самой себе.

Построим таблицу истинности для данного закона:

p	p→p
и	и
л	и

Независимо от того, принимает пропозициональная переменная p значение «истина» или «ложь», формула p→p имеет значение «истина».

Закон исключённого третьего, согласно которому два противоречащих друг другу суждения не могут быть одновременно истинными и одновременно ложными, имеет формулу pv~p.

Построим таблицу для данного закона:

p	~p	pv~p
и	л	и
л	и	и

Независимо от того, принимает пропозициональная переменная p значение «истина» или «ложь», формула pv~p имеет значение «истина».

Закон противоречия, согласно которому два противоположных суждения не могут быть одновременно истинными, по крайней мере, одно из них необходимо ложно, имеет формулу ~(p&~p).

Построим таблицу для данного закона:

p	~p	p&~p	~(p&~p)
и	л	л	и
л	и	л	и

Независимо от того, принимает пропозициональная переменная p значение «истина» или «ложь», формула ~(p&~p) имеет значение «истина».

Существуют также тождественно-ложные формулы или противоречия, которые принимают только значение «ложь».

Например, суждение «Она хорошо готовит, если и только если неверно, что она хорошо готовит». Формула данного суждения: p↔~p.

Данная формула имеет таблицу:

p	~p	p↔~p
и	л	л
л	и	л

Независимо от того, принимает пропозициональная переменная p значение «истина» или «ложь», формула p↔~p имеет значение «ложь».

Иногда различные по своей структуре формулы таковы, что одинаковым наборам логических значений переменных во входных столбцах таблиц этих формул отвечают одинаковые логические значения в соответствующих строках заключительных столбцов.

Например, в таблицах формул (p→~q) и ~(p&q)

p	q	~q	(p→~q)
и	и	л	л
л	и	л	и
и	л	и	и
л	л	и	и

p	q	p&q	~(p&q)
и	и	и	л
и	л	л	и
л	и	л	и
л	л	л	и

одинаковым наборам логических значений переменных p и q во входных столбцах отвечают одинаковые логические значения в соответствующих строках заключительных столбцов. О таких формулах говорят, что они равносильны.

Отношение равносильности, во-первых, рефлексивно, т.е. А равносильно А; во-вторых, симметрично, т.е. если А равносильно В, то В равносильно А; в-третьих транзитивно, т. е. если А равносильно В и В равносильно С, то А равносильно С.

Пусть А и В – формулы, Е1, Е2,…, Еn список всех пропозициональных переменных, входящих по крайней мере в одну из них. Будем говорить, что А и В – равносильные формулы, если при любых логических значениях Е1, Е2,…,Еn логические значения А и В совпадают.

Список равносильных формул:

(1) ~~A равносильно A;

(2) A&B равносильно B&A – закон коммунитативности конъюнкции;

(3) A&(B&C) равносильно (A&B)&C – закон ассоциативности конъюнкции;

(4) AvB равносильно BvA – закон коммутативности дизъюнкции;

(5) Av(BvC) равносильно (AvB)vC – закон ассоциативности дизъюнкции;

(6) Av(B&C) равносильно (AvB)&(AvC) – закон дистрибутивности дизъюнкции относительно конъюнкции;

(6') (B&C)vA равносильно (AvB)&(AvC) – закон дистрибутивности дизъюнкции относительно конъюнкции;

(7) A&(BvC) равносильно (A&B)v(A&C) – закон дистрибутивности конъюнкции относительно дизъюнкции;

(7') (BvC)&A равносильно (A&B)v(A&C) – закон дистрибутивности конъюнкции относительно дизъюнкции;

(8) A&A равносильно A – закон идемпотентности конъюнкции;

(9) AvA равносильно A – закон идемпотентности дизъюнкции;

(10) ~(A&B) равносильно ~Av~B – закон де Моргана;

(11) ~(AvB) равносильно ~A&~B – закон де Моргана;

(12) A&B равносильно ~(A→~B);

(13) A→B равносильно ~AvB;

(14) A&B равносильно ~(~Av~B);

(15) AvB равносильно ~(~A&~B);

(16) A↔B равносильно (~AvB)&(~BvA);

(17) A 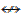B равносильно (AvB)&(~Av~B);

(18) (AvB)&(~AvB) равносильно B – закон исключения;

(19) A&(AvB) равносильно A – закон поглощения;

(20) Av(A&B) равносильно A – закон поглощения;

(21) (AvC)&(Bv~C) равносильно (AvC)&(Bv~C)&(AvB) – закон выявления;

(22) (A&C)v(B&~C) равносильно (A&C)v(B&~C)v(A&B) – закон выявления;

(23) A→B равносильно ~B→~A – закон контрапозиции;

(24) A↔B равносильно ~A↔~B;

(25) A 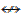B равносильно ~(A↔B);

(26) A↔B равносильно (A→B)&(B→A);

(27) A↔B равносильно (A&B)v(~A&~B);

(28) AvB равносильно ~A→B;

(29) A→B равносильно ~(A&~B);

(30) ~(A→B) равносильно A&~B;

(31) A↔B равносильно ~(~A 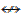~B);

(32) A 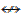B равносильно ~(~A↔~B);

(33) ~A↔B равносильно (~A 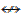~B);

(34) ~(A 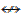B) равносильно (~A↔~B).

Знаки & и v, а также знаки ↔ и 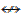являются двойственными логическими знаками.

Пусть А формула, в которую не входит знак →. Формулой, двойственной А, называют формулу А*, которая получается из А заменой каждого вхождения знаков & и ↔ соответственно двойственными им знаками v и 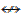и заменой каждого вхождения знаков v и 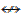в А соответственными им знаками & и ↔.

Например, если А – формула

(pvq)↔((p&r)v(q&r)),

То двойственная ей формула А* будет иметь вид

(p&q) ((pvr)&(qvr)).

Все приведённые равносильности можно доказать при помощи таблиц истинности.

Используя транзитивность отношения равносильности, зная о равносильности одних формул, можем судить о равносильности других.

Правило разрешающее в формуле А выделенное вхождение подформулы В заменять равносильной формулой В', называется правилом равносильной замены.

Например, надо доказать равносильность формул ~(pvq) и ~(~p→~~q).

~(pvq) равносильна (~p&~q) согласно равносильности (11)

(~p&~q) равносильна ~(~p→~~q) согласно равносильности (12)

Как уже было сказано каждая формула логики высказываний может быть или тождественно-истинной, или тождественно – ложной, или нейтральной. Тождественно-истинные и нейтральные формулы являются выполнимыми формулами. Выполнимая формула – формула логики высказываний, получающая значение «истина» хотя бы для одного набора логических значений своих переменных.

Задача, состоящая в отыскании процедуры, позволяющей для любой формулы выяснить, какому из трёх перечисленных выше классов она принадлежит, называется семантической проблемой разрешения для формул логики высказываний. В соответствии с этим процедура, позволяющая конечным числом простых действий решить проблему разрешения, называется разрешающей процедурой. Процесс построения по данной формуле отвечающей ей таблицы есть разрешающая процедура семантической проблемы разрешения для формул логики высказываний.

Впрочем, использовать табличный метод можно только в том случае, когда в формулу входит небольшое количество переменных и она не очень длинная. Для формул, содержащих большое количество переменных, существуют другие разрешающие процедуры.

Известно, что смысл разрешающей процедуры заключается в возможности отличить тождественно-истинные формулы от остальных.

Первым пунктом разрешающей процедуры является приведение к нормальной форме.

Формула логики высказываний имеет нормальную форму, если она: а) не содержит знаков →,↔, 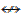и б) знаки отрицания стоят в ней только при переменных.

Например, формула (((pv~q)&r)v(~rvq)) имеет нормальную форму, а формула (~(p&q)v~r)v(~qvs) – нет.

Любую формулу А, не имеющую нормальной формы, можно преобразовать в формулу А', которая имеет нормальную форму.

Для того чтобы данную формулу привести к нормальной форме, необходимо произвести в ней следующие равносильные замены:

1) каждую подформулу вида (А 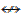В) заменить согласно равносильности (17) формулой ((AvB)&(~Av~B));

2) каждую подформулу вида (A↔B) заменить согласно равносильности (16) формулой ((~AvB)&(~BvA));

3) каждую подформулу вида (A→B) заменить согласно равносильности (13) формулой (~AvB);

4) каждую подформулу вида ~(A&B) заменить согласно равносильности (10) формулой (~Av~B);

5) каждую подформулу вида ~AvB заменить согласно равносильности (11) формулой (~A&~B);

6) каждую подформулу вида ~~A заменить согласно равносильности (1) формулой А.

Формула имеет нормальную форму, если ни один из перечисленных пп. 1) – 6) настоящего предписания к ней не применим.

Например, дана формула

(p 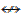q)→((p→r)→(q→r))

Четырежды применяя правило равносильной замены, согласно равносильности (13) получаем формулу

~(p 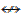q)v(~(~pvr)v(~qvr))

Из неё согласно равносильности (17) получаем формулу

~((pvq)&(~pv~q))v(~(~pvr)v(~qvr))

Из неё согласно равносильности (10) получаем формулу

~(pvq)v~(~pv~q)v(~(~pvr)v(~qvr))

Из неё согласно равносильности (11) получаем формулу

(~p&~q)v(~~p&~~q)v((~~p&~r)v(~qvr))

Трижды применяя правило замены, согласно равносильности (1) получаем следующую формулу в нормальной форме

(~p&~q)v(p&q)v((p&~r)v(~qvr))

Которую, пользуясь соглашением о бесскобочной записи кратной дизъюнкции, можно записать

(~p&~q)v(p&q)v(p&~r)v(~qvr)

Приведение к конъюнктивной нормальной форме (КНФ) позволяет по виду формулы, приведённой к некоторой стандартной форме, судить о том, тождественно-истинная она или нет.

Формула логики высказываний имеет КНФ, если она имеет вид

В1&B2&…&Bm,

Где В1, В2,…, Вm – элементарные дизъюнкции и m ≥ 1.

Элементарной дизъюнкцией называется формула, которая имеет вид

А1vА2v…vАn,

Где n ≥1, а Аi (i ≤ n ) есть или переменная, или отрицание переменной.

Для того чтобы формулу привести к КНФ, необходимо вначале с помощью известной процедуры привести её к нормальной форме. Затем каждую подформулу вида (Av(B&C)) согласно равносильности (6) и каждую подформулу вида ((B&C)vA) согласно равносильности (6') заменить формулой ((AvB)&(AvC)).

Например, формула (p→q)→(~pvq)

Приведём её вначале к нормальной форме:

(~pvq)→(~pvq) (13)

~(~pvq)v(~pvq) (13)

(~~p&~q)v(~pvq) (11)

(p&~q)v(~pvq) (1)

Затем, с помощью равносильности (6') получаем формулу

(~pvqvp)&(~pvqv~q),

Которая имеет КНФ. Данная формула является тождественно-истинной.

Формула, имеющая КНФ, тождественно-истинна тогда и только тогда, когда тождественно-истинны все её конъюнктивные члены, т.е. когда каждая элементарная дизъюнкция содержит хотя бы одну пару дизъюнктов, из которых один есть некоторая переменная, а другой – её отрицание.

Каждая не тождественно-истинная формула имеет КНФ, которая называется совершенной.

Совершенной конъюнктивной нормальной формой (СКНФ) некоторой формулы называется такая её КНФ, которая удовлетворяет следующим условиям:

a) в ней нет двух одинаковых конъюнктивных членов, и ни в одном конъюнктивном члене нет двух одинаковых дизъюнктов;

b) ни в одном конъюнктивном члене нет таких двух дизъюнктов, из которых один есть переменная, а другой – отрицание этой переменной;

c) в каждом конъюнктивном члене содержатся все переменные данной формулы.

Для того чтобы привести формулу к СКНФ необходимо:

1) Привести её к КНФ;

2) На основании равносильностей (2), (4), (8) устранить из КНФ повторяющиеся конъюнкты, т. е. из всех имеющихся одинаковых конъюнктивных членов оставить один и вычеркнуть остальные;

3) На основании равносильностей (4) и (9) устранить все повторения в конъюнктивных членах КНФ;

4) На основании равносильностей (2), (4) и (47) (AvИ (тождественно-истинная формула) равносильно А) устранить из КНФ те конъюнктивные члены, которые являются тождественно-истинными элементарными дизъюнкциями;

5) Ко всем тем конъюнктивным членам, в которых отсутствует какая-либо из содержащихся в данной формуле переменных Е, на основании равносильности (50) приписать знак дизъюнкции и вслед за ним тождественно-ложную конъюнкцию (Е&~Е), а затем применить правило замены по равносильности (6). Эту процедуру повторять до тех пор, пока в каждый конъюнктивный член не будут входить все переменные, содержащиеся в данной формуле;

6) Если в получившейся КНФ снова появились одинаковые конъюнктивные члены, то надо устранить повторения.

Процедура приведения формулы к СКНФ используется для отыскания логических следствий данных посылок.

Например, приведём к СКНФ формулу (p→q)v(~p&r)

Сначала приведём её к КНФ

(~pvq)v(~p&r) (13)

(~pvqv~p)&(~pvqvr)

Потом устраняем повторения в первом конъюнкте

(~pvq)&(~pvqvr)

Так как в первом конъюнктивном члене отсутствует переменная r, то присоединяем к нему знаком дизъюнкции формулу (r&~r)

(~pvqv(r&~r))&(~pvqvr)

Затем применяем равносильность (6) получаем формулу

(~pvqvr)&(~pvqv~r)&(~pvqvr)

Устраняем один из одинаковых конъюнктивных членов и получаем формулу в СКНФ:

(~pvqvr)&(~pvqv~r)

С помощью СКНФ можно получить обзор всех таких следствий из данных посылок, которые сами имеют СКНФ. Однако интерес представляют наиболее сильные следствия данных посылок. Формула А сильнее формулы В, а формула В слабее формулы А, если тождественно-истинна формула А→В, но не формула В→А. Поэтому представляют интерес простые следствия. Следствие В из посылок А1, А2,…, Аn называют простым, если В есть такая не содержащая повторений и не тождественно-истинная элементарная дизъюнкция, которая не «поглощается» никаким другим более сильным следствием из посылок А1, А2,…, Аn такого же вида. Простые следствия из данных посылок мы можем найти при помощи процедуры приведения к сокращённой КНФ.

Сокращённой КНФ данной формулы называется такая её КНФ, которая удовлетворяет следующим условиям:

а) ни в одном конъюнктивном члене нет двух одинаковых дизъюнктов;

б) ни в одном конъюнктивном члене нет таких двух дизъюнктов, из которых один есть переменная, а другой отрицание этой переменной;

в) нет таких пар конъюнктивных членов, что каждый дизъюнкт из одного имеется в другом, т.е. нет двух одинаковых конъюнктивных членов и нет таких двух конъюнктивных членов, из которых один поглощается другим;

г) если имеются такие два конъюнктивных члена, из которых один содержит некоторую переменную, а другой – её отрицание, то в той же КНФ имеется конъюнктивный член, который является элементарной дизъюнкцией, построенной из всех дизъюнктов данной пары, отличных от упомянутой переменной и её отрицания.

Для того чтобы привести формулу к сокращённой КНФ необходимо:

1) привести её к КНФ;

2) из всех одинаковых конъюнктивных членов КНФ оставить только один и в элементарных дизъюнкциях также устранить все повторения;

3) устранить все тождественно-истинные конъюнктивные члены;

4) если среди конъюнктивных членов КНФ имеются два таких, что один содержит некоторую переменную, а другой – её отрицание, то на основании закона выявления, необходимо добавить новый конъюнктивный член, являющийся дизъюнкцией остальных дизъюнктов этих двух конъюнктивных членов, а также, новый конъюнктивный член не должен быть тождественно-истинным и отличается от уже имеющихся;

5) применяя закон поглощения, равносильность (19), устраняем все поглощаемые конъюнктивные члены.

Например, даны посылки ~p→r, ~r→q, ~p→~r. Необходимо найти все их простые следствия. Приводим конъюнкцию посылок к КНФ:

(~p→r)&(~r→q)&(~p→~r)

(pvr)&(rvq)&(pv~r)&(qvp)&(pvp)

Устраняем повторения в новых конъюнктах

(pvr)&(rvq)&(pv~r)&(qvp)&p

Производим все поглощения:

(rvq)&p

Формулы (rvq) и p являются простыми следствиями данных посылок, т.е. если посылки истинны, то формула (rvq) – истинна, и p – истинна.

Формулы логики высказываний наряду с КНФ могут иметь дизъюнктивную нормальную форму (ДНФ).

Формула логики высказываний имеет дизъюнктивную нормальную форму, если она имеет вид В1, В2,…Вm, где В1, В2,…Вm – элементарные конъюнкции и m ≥ 1.

Элементарной конъюнкцией называется формула, которая имеет вид А1, А2,…, Аn, где n ≥ 1, Аi (I ≤ n) – либо переменная, либо отрицание переменной.

Для того чтобы привести формулу к ДНФ, необходимо привести её вначале к нормальной форме. Затем каждую подформулу вида (A&(BvC)) согласно равносильности (7) и каждую подформулу вида ((BvC)&A) согласно равносильности (7') заменить формулой ((А&B)v(A&C)).

Например, надо привести к ДНФ формулу (((p→q)→(q→r))&(~rvp)).

Сначала приводим её к нормальной форме:

((p&~q)v(~qvr))&(~rvp)

Затем приводим к ДНФ:

(((~rvp)&(p&~q))v((~rvp)&(~qvr)))

(p&~q&~r)v(p&~q&p)v(((~rvp)&~q)v((~rvp)&r)))

(p&~q&~r)v(p&~q&p)v(~q&~r)v(~q&p)v(r&~r)v(r&p)

Данная формула не является тождественно-ложной, так как только один дизъюнктивный член содержит пару конъюнктов, из которых один есть переменная, а другой – её отрицание (r&~r). Если бы все дизъюнктивные члены содержали бы пару конъюнктов, из которых один есть переменная, а другой – её отрицание, то формула была бы тождественно-ложной.

Каждая не тождественно-ложная формула имеет ДНФ, которая называется совершенной.

Совершенной ДНФ (СДНФ) некоторой формулы называется её ДНФ, которая удовлетворяет следующим условиям:

а) в ней нет двух одинаковых дизъюнктивных членов, и ни в одном дизъюнктивном члене нет двух одинаковых конъюнктов;

б) ни в одном дизъюнктивном члене нет таких двух конъюнктов, из которых один есть переменная, а другой – отрицание этой переменной;

в) в каждом дизъюнктивном члене содержатся все переменные данной формулы.

Для того чтобы привести формулу к СДНФ, необходимо:

1) привести её к ДНФ;

2) на основании равносильностей (2), (4) и (9) устранить из ДНФ повторяющиеся дизъюнкты;

3) на основании равносильностей (2) и (8) устранить все повторения в дизъюнктивных членах ДНФ;

4) на основании равносильностей (2), (4) и (50) устранить из формулы те дизъюнктивные члены, которые являются тождественно-ложными элементарными конъюнкциями;

5) ко всем тем дизъюнктивным членам, в которых отсутствует какая-нибудь из содержащихся в данной формуле переменных Е, на основании равносильности (47) приписать знак конъюнкции, вслед за ним – тождественно-истинную дизъюнкцию (Еv~Е) и применить правило замены по равносильности (7). Эту процедуру повторять до тех пор, пока не окажется, что в каждый дизъюнктивный член входят все переменные, содержащиеся в данной формуле. Если в формуле снова появились одинаковые дизъюнктивные члены, то надо устранить повторения.

С помощью СДНФ можно получить обзор всех гипотез данной формулы, которые имеют СДНФ.

Гипотезой формулы В называют такую формулу А, что формула А→В тожденственно-истинна.

Например, приведём формулу (q&(~rvs)) к СДНФ.

Вначале приведём её к ДНФ:

(q&~r)v(q&s)

Пополняем оба дизъюнкта недостающими переменными:

((q&~r)&(sv~s))v((q&s)&(rv~r))

(q&~r&s)v(q&~r&~s)v(q&s&r)v(q&s&~r)

Устраняем возникшие повторения и получаем СДНФ данной формулы:

(q&~r&~s)v(q&s&r)

С помощью сокращенной ДНФ можно найти все простые гипотезы формулы. Гипотеза А формулы В называется простой, если А есть элементарная конъюнкция, которая не тождественно-ложная, не содержит повторений и не поглощается никакой другой, более слабой, гипотезой формулы В такого же вида.

Сокращённой ДНФ данной формулы называется такая её ДНФ, которая удовлетворяет следующим условиям:

а) ни в одном дизъюнктивном члене нет двух одинаковых конъюнктов;

б) ни в одном дизъюнктивном члене нет таких двух конъюнктов, из которых один есть переменная, а другой – отрицание этой переменной;

в) нет двух одинаковых дизъюнктивных членов и нет таких двух членов, из которых один поглощается другим;

г) если имеются такие два дизъюнктивных члена, из которых один содержит некоторую переменную, а другой – её отрицание, то в этой же ДНФ имеется дизъюнктивный член, который является элементарной конъюнкцией, построенной из всех конъюнктов данной пары, отличных от упомянутой переменной и её отрицания.

Для того чтобы привести формулу к сокращённой ДНФ нужно произвести следующие преобразования:

1) привести её к ДНФ;

2) во всех дизъюнктивных членах ДНФ и в элемнтарных конъюнкциях устранить все повторения;

3) устранить из ДНФ все тождественно-ложные дизъюнктивные члены;

4) если среди дизъюнктивных членов ДНФ имеются два таких, что один содержит некоторую переменную, а другой – её отрицание, то на основании закона выявления, т.е. равносильности (22), добавить новый дизъюнктивный член, представляющий собой конъюнкцию остальных конъюнктов этих двух дизъюнктивных членов, при условии, что новый дизъюнктивный член не тождественно-ложный и отличается от всех остальных;

5) снова устранить повторения в новых дизъюнктивных членах ДНФ;

6) если среди дизъюнктивных членов ДНФ имеются такие, которые поглощаются другими, то по равносильности (20), устраняются все поглощаемые дизъюнктивные члены.

Например, дана формула (((p&q)v(r&s))→~(p&~q&r)). Необходимо найти все простые гипотезы данной формулы.

Сначала приводим её к ДНФ:

(~((p&q)v(r&s))v~(p&~q&r))

((~(p&q)&~(r&s))v(~pvqv~r))

(((~pv~q)&(~rv~s))v~pvqv~r)

((((~pv~q)&~r)v((~pv~q)&~s))v~pvqv~r)

(~r&~p)v(~r&~q)v(~s&~p)v(~s&~q)v~pvqv~r

Затем приводим полученную формулу к сокращённой ДНФ:

~pv~rv(~s&~q)vq

~pv~rv(~s&~q)vqv~s

~pv~rv~svq

Таким образом, данная формула логически следует из гипотезы ~p, или гипотезы ~r, или гипотезы ~s, или гипотезы q.

Контрольные вопросы:

1. Дайте определение логики высказываний.

2. Какие формулы называются тождественно-истинными?

3. В чём отличие между законом исключённого третьего и законом противоречия?

4. Как Вы думаете, почему при ложности антецедента и истинности консеквента, импликация принимает значение «истина»?

5. В чём заключается смысл процедуры приведения формулы к нормальной форме?

6. Какие логические знаки являются двойственными?

7. Укажите преимущества и недостатки построение таблицы истинности для данной формулы как разрешающей процедуры семантической проблемы разрешения.