Суперпозиция функций алгебры логики
Суперпозиция – основная операция, которую можно производить над логическими функциями. Суперпозиция – это образование новой функции из нескольких исходных.
Строгое определение суперпозиции дается по индукции.
Определение. Пусть  - конечная система логических функций. Функция
- конечная система логических функций. Функция  называется элементарной суперпозицией или суперпозицией ранга 1 функций системы
называется элементарной суперпозицией или суперпозицией ранга 1 функций системы  , если она получена одним из следующих способов
, если она получена одним из следующих способов
а. Из какой-либо функции  переименованием какой-то из ее переменных xij, буква xij заменяется некоторой буквой y. В этом случае
переименованием какой-то из ее переменных xij, буква xij заменяется некоторой буквой y. В этом случае  . В частности, буква y может совпадать с одной из переменных xis функции
. В частности, буква y может совпадать с одной из переменных xis функции  . Тогда говорят об отождествлениипеременных xij и xis.
. Тогда говорят об отождествлениипеременных xij и xis.
Пример. Пусть  . Тогда
. Тогда 


 - это суперпозиции ранга 1;
- это суперпозиции ранга 1;
б. Подстановкой некоторой функции  вместо какого-то аргумента xij одной из функций
вместо какого-то аргумента xij одной из функций  .
.
Тогда  . Эта функция зависит от аргументов xi1,…, xij-1, xij+1,…,
. Эта функция зависит от аргументов xi1,…, xij-1, xij+1,…,  , xr1,…,
, xr1,…,  .
.
Пример. В условиях предыдущего примера функции  ,
,  ,
,  , - это суперпозиции ранга 1.
, - это суперпозиции ранга 1.
Определение. Суперпозиции ранга 1 образуют класс  , суперпозиций ранга 1. Суперпозиции ранга 1 функций из множества
, суперпозиций ранга 1. Суперпозиции ранга 1 функций из множества  образуют класс
образуют класс  ,…, суперпозиции ранга 1 функций из множества
,…, суперпозиции ранга 1 функций из множества  образуют класс
образуют класс  суперпозиций ранга p+1 функций исходной системы
суперпозиций ранга p+1 функций исходной системы  .
.
Определение. Суперпозицией функций из системы  называется всякая функция, входящая в какой-либо из классов
называется всякая функция, входящая в какой-либо из классов  , р=0,1,2,…. Здесь
, р=0,1,2,…. Здесь  - исходная система функций (суперпозиции ранга ноль).
- исходная система функций (суперпозиции ранга ноль).
Пример. Функции  ,
,  ,
,  ,
,  ,
,  - это суперпозиции функции системы
- это суперпозиции функции системы 
Замечание 1. Если функции  и
и  имеют одинаковые таблицы истинности, отличаясь только обозначениями переменных, то каждая из них является суперпозицией другой.
имеют одинаковые таблицы истинности, отличаясь только обозначениями переменных, то каждая из них является суперпозицией другой.
Замечание 2. 
Замечание 3. Если все функции исходной системы  обладают некоторым свойством, которое наследуется всякой суперпозицией ранга 1, то этим свойством обладают все функции из системы
обладают некоторым свойством, которое наследуется всякой суперпозицией ранга 1, то этим свойством обладают все функции из системы  ,…, системы
,…, системы  ,…, все суперпозиции функций из
,…, все суперпозиции функций из  .
.
Замечание 4. Описывая правила построения формулы, мы неявно пользовались понятием суперпозиции, ведь всякая формула - это суперпозиция функций  x~y,
x~y,  и символов констант 0 и 1.
и символов констант 0 и 1.
Примеры решения задач.
Пример 1.
Доказать равносильности:  (один из законов де Моргана);
(один из законов де Моргана);
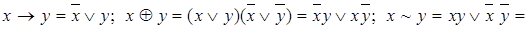
= 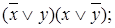
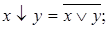 x|y =
x|y = 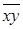 .
.
Решение. Составим таблицу истинности некоторых из указанных функций (табл. 7).
Таблица 7
| x | y | x→y |  | x~y |  |  |  |  |  |
Пример 2. Преобразовать данную формулу к равносильной формуле, в которой отрицания стоят только над аргументами:  .
.
Решение.  .
.
Пример 3. Упростить формулу:  .
.
Решение  Пример 4. Составить таблицу истинности формулы:
Пример 4. Составить таблицу истинности формулы:

Решение(табл. 8).
Таблица 8
| x | y | z |  |  |  |  | |  |  |  |  |
Пример 5.
Функции  и
и  заданы таблицами истинности (табл. 9, табл. 10). Построить таблицу истинности суперпозиции
заданы таблицами истинности (табл. 9, табл. 10). Построить таблицу истинности суперпозиции
 .
.
Таблица 9 Таблица 10
 |  |  |  |  |  | |
Решение. Построим таблицу истинности функции  (табл. 11).
(табл. 11).
Таблица 11
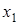 | 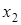 |  |  |  |  |
