Существенные и несущественные переменные

Основы алгебры логики

Основные определения

Определение. Функцией алгебры логики (логической функцией, булевой функцией) n переменных f(x₁,…, x_n) называется функция, принимающая значения 0 или 1, аргументы которой также принимают значения 0 или 1. Константу 1 по-другому называют истиной, а константу 0 − ложью.

Аргументы логической функции называют логическими (булевыми)

переменными.

Итак, если 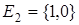, то 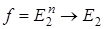- это логическая функция n переменных.

Булеву функцию n переменных можно задать таблицей истинности вида (табл. 1)

Таблица 1

x1	x2	...	xn-1	xn	f(x1,…, xn)
		...			0 или 1
		...			0 или 1
		...			0 или 1
...	...	...	...	...	0или 1
		...			0 или 1

Таблица истинности функции n переменных содержит 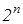строк, в которых записаны 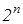разных возможных наборов значений аргументов функции (такие наборы называются двоичными наборами длины n). Число 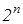получается по принципу умножения: чтобы задать двоичный набор длины n нужно выполнить n действий, каждое из которых можно выполнить двумя способами – приписать очередной переменной значение 0 или 1.

Каждому набору значений аргументов можно поставить в соответствие два варианта значений функции на этом наборе – 0 или 1. Таким образом, число различных булевых функций n переменных равно 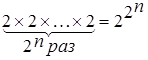и очень быстро растет с ростом n.

Если n=1, то 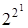= 2² = 4; если n = 2, то 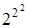= 16; если n = 3, то 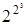= 256.

Итак, двоичный набор – это упорядоченная энка, элементы которой – цифры 0 или 1. В записи двоичного набора их можно не разделять запятыми.

Всякий двоичный набор 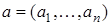можно рассматривать как натуральное число, записанное в двоичной системе счисления, это число называется номером набора. Например,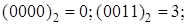

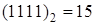. Номера наборов - это натуральные числа от 0 до 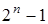. Набор с номером 0 называется нулевым, потому что содержит одни нули. Набор с номером 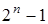называется единичным, его составляют только единицы. В таблице истинности наборы значений переменных располагаются в порядке возрастания номеров, от нулевого к единичному. Поэтому задать логическую функцию можно одним столбцом ее значений, после чего таблица истинности однозначно восстанавливается. Столбец значений функции, превращенный в строку, называется вектором значений.

Существенные и несущественные переменные.

Говорят, что функция f(x₁,...,x_n) существенно зависит от переменной x_i ,если существует такой набор 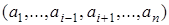значений других аргументов, что 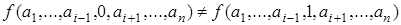. В этом случае переменная x_i называется существенной переменной, в противном случае x_i называется несущественной (фиктивной) переменной.

Пример. Пусть булевы функции f₁(x,y) и f₂(x,y), f₃(x,y), f₄(x,y) заданы таблицей истинности (табл. 2)

Тогда y – фиктивная переменная функции f₁, x - фиктивная переменная функции f₂, как x, так и y – несущественные переменные функции f₃, а

функция f₄ существенно зависит от обоих своих аргументов.

Таблица 2

x	y	f1(x,y)	f2(x,y)	f3(x,y)	f4(x,y)