Пример реализации логических функций в базисе Жегалкина

Таблица 2.5 – Таблица истинности булевой функции трех переменных

x1	x2	x3	y

Для данной таблицы истинности после преобразований была получена следующая функция в операторной форме:

.

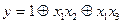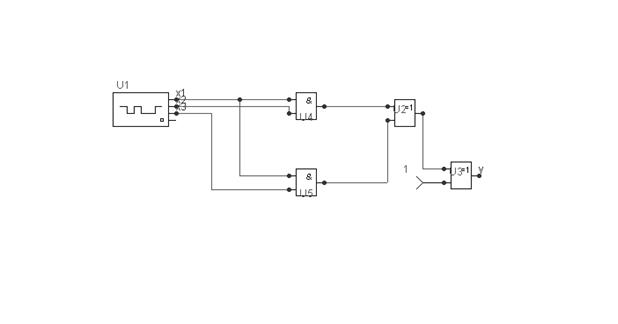
Рисунок 2.4 - Комбинационная схема, реализующая функцию заданную таблицей 2.2.

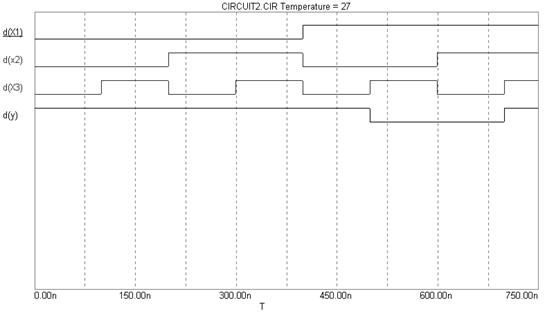
Рисунок 2.5 – Временная диаграмма работы схемы, изображенной на рисунке 2.4

2.6 Содержание отчета

Отчет должен содержать краткие теоретические сведения, необходимые для выполнения заданий и ответа на контрольные вопросы, все схемы, таблицы, диаграммы, полученные при выполнении задания, а также выводы по работе.

2.7 Контрольные вопросы

1. Сформулируйте определение логической функции, конституенты, импликанты и простой импликанты функции.

2.Что такое совершенная, сокращенная, тупиковая и минимальная ДНФ (КНФ)?

3.Дайте определение функциональной полноты булевых функций.

4.В чем заключается сущность минимизации булевых функций?

5.Охарактеризуйте основные этапы синтеза комбинационных схем.

6.Какова специфика синтеза комбинационных схем с несколькими выходами ?

7.Как осуществляется развязка схем по коэффициентам объединения и разветвления логических элементов?

3 ЛАБОРАТОРНАЯ РАБОТА № 3

ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ ТРИГГЕРОВ

3.1 Цель работы

3.1

Изучить принципы фуцнкционирования триггеров различных типов, овладеть методами их проектирования.

3.2 Основные положения

Триггер представляет собой устройство с двумя устойчивыми состоя- ниями и широко используется в цифровых схемах в качестве запоминающего элемента.

Триггеры отличаются как по функциональному признаку, так и по способу записи информации.

Среди множества функциональных типов триггеров,которые находят широкое применение можно выделить RS, D, DV, JK, T, RSR, RSS, RSE триггеры. Способ функционирования триггеров может быть описан таблицею переходов, характеризующей состояния входов и выходов триггера в момент времени до его срабатывания (t ^s) и после его срабатывания (t ^s+1) .

Из таблицы переходов RS – триггера (таблица 4.1) следует, что триггер не меняет своего состояния в момент t ^s+1 (Q ^s+1 = Q ^s), если в момент времени t ^s имеет место R ^s = 0 и S ^s = 0.

При комбинации сигналов R ^s = 0, S ^s = 1 триггер устанавливается в единичное состояние (Q ^s+1 = 1), а при комбинации R ^s = 1, S ^s = 0 в нулевое

(Q ^s+1 = 0).

При R ^s = 1, S ^s = 1 состояние триггера не определено (Q ^s+1 = *). Такая комбинация сигналов для RS - триггера является запрещенной.

RSR - триггер отличается от RS - триггера тем, что при комбинации входных сигналов R ^s = S ^s = 1 он переходит в нулевое состояние (Q ^s+1 = 0). RSS - триггер в этом случае переходит в единичное состояние (Q ^s+1 = 1), а RSЕ - триггер не изменяет своего состояния (Q ^s+1 = Q ^s).

D - триггер называют триггером эадержки (таблица 4.2). Он осуществляет задержку входного сигнала, поступающего на информационный вход (D - вход). Для такого триггера справедливо равенство Q ^s+1 = D ^s .

DV - триггер отличается от D - триггера тем, что имеет дополнительный вход V (таблица 4.3 ). При V = 1 DV - триггер работает как D - триггер, а при V = 0 - не изменяет своего состояния.

Таблица 4.1 – Переходы RS, RSR, RSS, RSE триггеров

t s	t S+1
R s	S s	Q s+1
RS	RSR	RSS	RSE
		Q s	Q s	Q s	Q s
		*			Q s

Таблица 4.2 – Переходы D - триггерa

t s	t S+1
D s	Q s+1

Таблица 4.3 – Переходы DV - триггерa

t s	t S+1
D s	V s	Q s+1
		Q s
		Q s

Таблица 4.4 – Переходы T - триггерa

t s	t S+1
T s	Q s+1
	Q s

Т- триггер называют также счетным триггером. Он осуществляет подсчет единиц, поступающих на вход Т, по модулю два, что видно из таблицы 4.4.

Из таблицы переходов JK – триггера (таблица 4.5) следует, что при комбинации входных сигналов J = K = 1 он изменяет свое состояние на противоположное, то есть работает как счетный триггер, а при остальных комбинациях он работает как RS - триггер.

Таблица 4.5 – Переходы JK - триггерa

t s	t S+1
J s	K s	Q s+1
		Q s

Классификация по способу записи разделяет триггеры на асинхронные и синхронные.

У асинхронных триггеров имеются только информационные входы. Запись информации в асинхронные триггеры осуществляется непосредственно с поступлением информационных сигналов.

Синхронные триггеры имеют тактирующие входы. Синхронизирующие (тактирующие) сигналы задают частоту смены информации в дискретные моменты времени.

Различают следующие типы синхронных триггеров:

- управляемые уровнем тактирующего сигнала,

- управляемые перепадом тактирующего сигнала

Триггеры первого типа при появлении тактирующего сигнала могут переключаться столько раз, сколько раз изменяются информационные сигналы. Другими словами ,синхронные триггеры при активном состоянии тактирующего сигнала ведут себя подобно асинхронным.

В триггерах второго типа выходные сигналы, соответствующие новому состоянию триггера, появляются только в момент перехода тактирующего сигнала из 0 в 1 или наоборот.

MS схема всегда срабатывает по заднему фронту (при снятии активного уровня) тактирующего сигнала, т.е. на элементах ИЛИ-НЕ при переходе из 0 в 1, а на элементах И-НЕ при переходе из 1 в 0.

Схема же трех триггеров всегда срабатывает по переднему фронту (при подаче) синхроимпульса, т.е. на ИЛИ-НЕ при переходе из 1 в 0, а на И-НЕ при переход из 0 в 1.

Проектирование триггерных устройств состоит в выборе запоминающего элемента (ЗЭ) (рисунок 4.1) и синтезе схемы управления (СУ), реализующей функции возбуждения f₁ и f₂ в заданном элементном базисе.

Рисунок 4.1 – Структура триггера

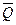Если в столбце Q ^s+1 таблицы переходов проектируемого триггера имеется значение , то сигналы на выходах Q и триггера являются аргументами функций f₁ и f₂ , поэтому в этом случае используют ЗЭ с внутренней задержкой. Аналогичная ситуация возникает и в том случае, когда аргументами функций f₁ и f₂ являются сигналы на выходах Q и 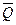других триггеров, переключающихся в процессе работы одновременно с данным триггером.

Наибольшее распространение среди ЗЭ триггеров с внутренней задержкой получили:

- МS схема с инвертором в цепи тактирования,

- MS схема с запрещающими связями,

- ЗЭ по схеме трех триггеров.

MS схема с инвертором в цепи тактирования, представлена на рисунке 4.2.

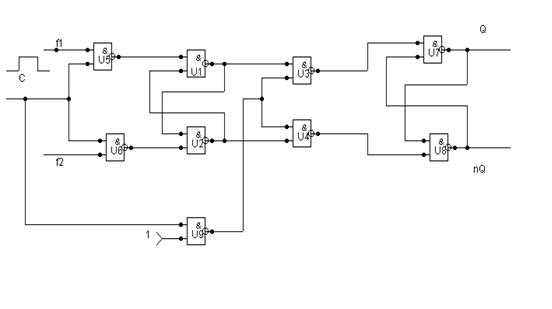
Рисунок 4.2 – MS схема с инвертором в цепи тактирования

на элементах И - НЕ

На рисунке 4.3 представлен запоминающий элемент, который выполнен

по MS схеме с запрещающими связями.

Рисунок 4.3 – MS схема с запрещающими связями

на элементах И - НЕ

Подграфы переходов этих ЗЭЗЭ одинаковы.

Таблица 4.6 – Подграфы переходов ЗЭЗЭ по МS схеме на элементах И - НЕ

	f 1	f 2
		─
	─

Примечание: знаком «─» отмечены произвольные значения функций возбуждения f ₁ и f ₂.

Аналогичные ЗЭЗЭ можно построить и на элементах ИЛИ – НЕ. Структура их ничем не отличается от схем на элементах И – НЕ. Подграфы переходов этих схем представлены в таблице 4.7.

Таблица 4.7 – Подграфы переходов ЗЭЗЭ по МS схеме на элементах ИЛИ - НЕ

	f 1	f 2
	─
		─

Еще одним типом ЗЭЗЭ, управляемых перепадом тактирующего сигнала, являются ЗЭЗЭ по схеме трех триггеров.

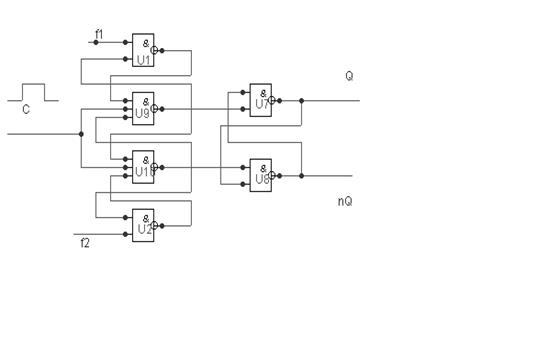
Рисунок 4.4 – ЗЭ по схеме трех триггеров на элементах И – НЕ

Его подграфы переходов представлены в таблице 4.8.

Таблица 4.8 – Подграфы переходов ЗЭЗЭ по схеме трех триггеров на элементах И - НЕ

	f 1	f 2
		─
	─

Аналогичный ЗЭ можно построить на элементах ИЛИ – НЕ.

Таблица 4.9 – Подграфы переходов ЗЭЗЭ по схеме трех триггеров на элементах ИЛИ - НЕ

	f 1	f 2
	─
		─

Перед синтезом схемы управления (СУ) необходимо определить, при каких значениях f ₁ и f ₂ триггер осуществляет определенные переходы из одного состояния в другое. Для этого на основании таблицы переходов триггера строится полная таблица переходов, в которой отражают также значение Q ^s в момент времени t ^s и, при необходимости значение С. Из полной таблицы переходов получают выражение для f ₁ и f _2. Затем выполняют минимизацию полученных функций и реализуют их на заданных элементах.

3.3 Пример построения DV-триггеров по MS схеме на элементах И-НЕ

Таблица 4.10 - Полная таблица переходов DV-триггера

D	V	QS	QS+1

На основании таблицы переходов и подграфа переходов ЗЭ по MS -схеме составим таблицу истинности для функций возбуждения ЗЭ.

Таблица 4.11 - Таблица истинности для функций возбуждения ЗЭ

D	V	QS	f1	f2
				—
			—
				—
				—
			—
			—

Произведём минимизацию функций возбуждения.

Таблица 4.12 - Минимизацию функций возбуждения для построения DV-триггера

D\VQs
		—
		—	—

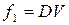
D\VQs
	—			—
	—

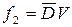
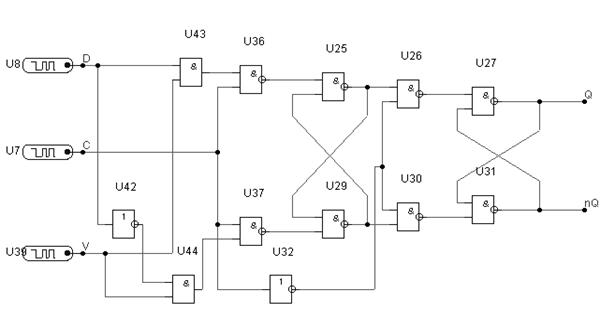
Рисунок 4.5 - Комбинационная схема DV-триггера по MS-схеме на И-НЕ

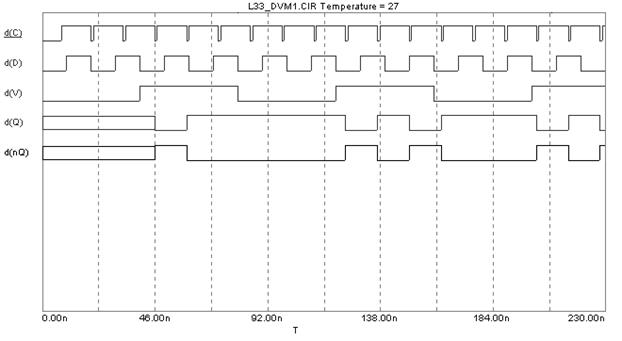
Рисунок 4.6 – Диаграммы для комбинационной схемы DV-триггера по MS-схеме на И-НЕ

3.4 Задания для домашней подготовки

1. Построить и начертить в протоколе триггеры, управляемые уровнем тактирующего сигнала на элементах И-НЕ и ИЛИ-НЕ по таблицам переходов ( таблица 4.1).

2. Построить и начертить в протоколе триггеры, управляемые перепадом тактирующего сигнала на элементах И-НЕ и ИЛИ-НЕ по MS схеме и по схеме трех триггеров в соответствии с таблицами переходов (таблицы 4.2, 4.3, 4.4, 4.5). Для всех шестнадцати полученных схем определить, по какому фронту тактирующего сигнала осуществляется переключение триггера.

3.Построить и начертить триггер по MS схеме на элементах ИЛИ-НЕ и по схеме трех триггеров на элементах И-НЕ в соответствии с таблицей вариантов (таблица 4.7). Номер варианта соответствует порядковому номеру в журнале.

Таблица 4.7 – Варианты заданий

t s

t S+1

x1

x2

Q S+1

Варианты

QS

QS

QS

QS

QS

QS

QS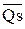

QS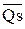

QS

QS

QS

QS

QS

QS

QS

QS

QS

QS

QS

QS

QS

QS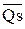

QS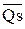

QS

QS

QS

QS

QS

QS

QS

3.5 Порядок выполнения работы

1. Подготовить схемы всех указанных выше триггеров.

2. По указанию преподавателя показать указанные схемы и их диаграммы работы.

3.6 Содержание отчета

Отчет должен содержать краткие теоретические сведения, необходимые для выполнения работы, таблицы, схемы и диаграммы, полученные при выполнении работы, а также выводы по работе.

3.7 Контрольные вопросы

1. Составьте таблицы переходов RS, RSR, RSS, RSE, D, T, DV и JK триггеров.

2. В чем различие между синхронными и асинхронными триггерами?

3. В чем различие между синхронными триггерами, управляемыми уровнем тактирующего сигнала и синхронными триггерами, управляемыми перепадом тактирующего сигнала?

4. Объяснить работу синхронных триггеров, выполненных по MS схеме и по схеме трех триггеров.

5. Охарактеризуйте этапы проектирования триггеров.

6. Как построить Т – триггер на основе D и JK триггеров?

4 ЛАБОРАТОРНАЯ РАБОТА № 4

ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ

СИНХРОННЫХ АВТОМАТОВ

4.1 Цель работы

4.1

Изучить методы проектирования и отладки цифровых синхронных автоматов Мура и Мили.

4.2 Основные положения

4.2

Для задания автомата необходимо описать все элементы множества S = {A, X, Y, d, l, a0}, т.е.

· алфавит состояний А = {а0 ... аk}, где а0 - начальное состояние автомата,

· входной алфавит Х = {х1 ... хn},

· выходной алфавит Y = {y1 ... ym},

· функцию переходов d и выходов l.

С этой целью наиболее часто используют табличный или графический способы задания. На этом и завершается первый этап синтеза автоматов.

Однако, автомат может содержать лишние внутренние состояния и

поэтому необходимо провести минимизацию числа состояний автомата.

Основная идея одного из методов минимизации состоит в разбиении

всех состояний исходного автомата на попарно не пересекающиеся классы эквивалентных состояний и замене каждого класса эквивалентности одним состоянием. Таким образом, получающийся в результате минимальный автомат имеет столько же состояний, на сколько классов эквивалентности разбиваются состояния исходного автомата.

Два состояния а_m и а_s называются эквивалентными (а_m º а_s), если (а_m, e) = (а_s, e) для всевозможных входных слов e. Если а_m и а_s не эквивалентны, они различимы.

Введем понятие k эквивалентности. Два состояния а_m и а_s k – экви- валентны, если l (а_m, e_k) = l (а_s, e_k) для всевозможных входных слов длины k, если состояния не k - эквивалентны, они k - различимы. Приведенные ношения эквивалентности и k - эквивалентности используются для разбиения множества состояний автомата на попарно не пересекающиеся классы (классы эквивалентности). Соответствующие разбиения на классы эквивалентности и k-эквивалентности будем обозначать p и p_k .Разбиение p позволяет определить избыточные элементы в множестве состояний автомата.

Минимизация числа состояний автомата состоит из следующих шагов.

1. Находятся последовательные разбиения p₁, p₂ ... p_k, p_k+1 мно- жества состояний на классы до тех пор, пока на каком-то k+1 шаге не окажется p_k+1 = p_k .B этом случае p_k = p , т.е. k-эквивалентные состояния являются в этом случае эквивалентными.

2. В каждом классе эквивалентности разбиения p выбирается по одному элементу, которые образуют новое множество состояний мини- мального автомата.

3. Для определения функций переходов и выходов вычеркиваются строки не вошедшие в множество состояний минимального автомата. А в оставшихся строках таблицы переходов все состояния заменяются на эквивалентные из нового минимального множества состояний автомата.

Рассмотрим на примере минимизацию числа состояний автомата Мили, заданного таблицей переходов (таблица 5.1) и таблицей выходов (таблица 5.2).

Непосредственно по таблице выходов (таблица 5.2) получим разбиение p₁ на классы одноэквивалентных состояний, объединяя в эквивалентные классы одинаковые строки p₁ = {B₁, B₂}, B₁ = {a₁, a₂, a₅, a₆},

B₂ = {a₃, a₄}.

Таблица 5.1 – Таблица переходов Таблица 5.2 – Таблица выходов

А	х 1	х 2		А	х 1	х 2
а 1	а 3	а 5		а 1	y 1	y 1
а 2	а 4	а 6		а 2	y 1	y 1
а 3	а 3	а 5		а 3	y 1	y 2
а 4	а 4	а 6		а 4	y 1	y 2
а 5	а 5	а 1		а 5	y 1	y 1
а 6	а 6	а 2		а 6	y 1	y 1

Построим таблицу для p₁ (таблица 5.3), заменяя состояния в таблице переходов соответствующими классами 1 – эквивалентных состояний.

По приведенной таблице получаем разбиение p₂ на классы 2 – экви- валентных состояний (таблица 5.4), где p₂ = {С₁, C₂, C₃}, C₁ = {a₁, a₂},

C₂ = {a₅, a₆}, C₃ = {a₃, a₄} .

Таблица 5.3 – 1–эквивалентности Таблица 5.4 – 2-эквивалентности

p1	х 1	х 2			p2	х 1	х 2
В 1	а 1	B 2	B 1			C 1	а 1	C 3	C 2
а 2	B 2	B 1			а 2	C 3	C 2
а 5	B 1	B 1			C 2	а 5	C 2	C 1
а 6	B 1	B 1			а 6	C 2	C 1
В 2	а 3	B 2	B 1			C 3	а 3	C 3	C 2
а 4	B 2	B 1			а 4	C 3	C 2

Производим разбиение p₃, которое совпадает с p₂. Поэтому про- извольно выберем из каждого класса С₁, C₂ и С₃ по одному состоянию и получаем таблицу переходов (таблица 5.5) и таблицу выходов (таблица 5.6) минимального автомата Мили.

Таблица 5.5 – Таблица переходов Таблица 5.6 – Таблица выходов

А	х 1	х 2		А	х 1	х 2
а 1	а 4	а 5		а 1	y 1	y 1
а 4	а 4	а 5		а 4	y 1	y 2
а 5	а 5	а 1		а 5	y 1	y 2

Минимизация числа состояний автомата Мура проводится аналогично.

Канонический метод структурного синтеза позволяет свести зада- чу синтеза произвольного автомата к задаче синтеза комбинационных схем.

Канонический метод синтеза условно можно разделить на следующие этапы:

· кодирование,

· выбор элементов памяти,

· построение булевых функций выходов автомата и возбуждения элементов памяти,

· построение функциональной схемы автомата.

При переходе на структурный уровень представления, каждая буква x _i входного алфавита X, каждая буква y _i выходного алфавита Y, каждая буква а_i алфавита состояний А представляется двоичным вектором.

Число сигналов, необходимых, например, для кодирования внутренних состояний автомата, определяется по формуле:

k_c ³ ] log ₂ │A│ [ ,

где ] М [ - обозначает наименьшее целое число, большее или равное М,

│А│-мощность алфавита состояний автомата, например, если

А = {а₁, а₂, а₃}, то │А│ = 3.

Если у автомата 3 состояния, то k ³ 2. Иными словами, каждую букву а_i c А можно закодировать двоичным вектором, состоящим не менее чем из двух компонент, например, А = {00, 01, 10}.

Пусть задан автомат Мили с помощью таблицы переходов (таблица 5.7) и таблицы выходов (таблица 5.8).

Мы видим, что минимальное число входных каналов k _вх = 1, так как │X│= 2, а k_вых = ]log₂ 2[ = 1. Иными словами, каждую букву x₁, x₂ можно закодировать двоичным вектором, состоящим из одной компоненты, т.е.

X = {0, 1}.

Таблица 5.7 – Таблица переходов Таблица 5.8 – Таблица выходов

Состояния автомата	Входные сигналы		Состояния автомата	Входные сигналы
х 1	х 2		х 1	х 2
а 1	а 2	а 1		а 1	y 1	y 3
а 2	а 1	а 2		а 2	y 2	y 4
а 3	а 3	а 2		а 3	y 1	y 2

Каждую букву y _i выходного алфавита тоже представим как двоичный вектор, число компонент которого k_вых = 2, т.е. равно числу физически реализуемых выходных каналов автомата. Y = {00,01,10,11}. Отметим, что в общем случае каждой кодируемой букве может быть приписан произвольный двоичный вектор, но обязательно две различные буквы одного и того же алфавита должны кодироваться различными двоичными векторами.

Закодированные таблицы переходов (таблица 5.9) и выходов (таблица 5.10) представлены ниже.

Таблица 5.9 – Таблица переходов Таблица 5.10 – Таблица выходов

Состояния	Входные сигналы		Состояния	Входные сигналы
Q 1 Q 2	х = 0	х = 1		Q 1 Q 2	х = 0	х = 1
0 0	0 1	0 0		0 0	0 0	1 0
0 1	0 0	0 1		0 1	0 1	1 1
1 0	1 0	0 1		1 0	0 0	0 1

Различны варианты кодирования состояний автомата приводят к различным выражениям функций выходов, в результате чего оказывается что сложность комбинационных схем автомата существенно зависит от выбранного метода кодирования.

Рассмотрим эвристический алгоритм кодирования состояний автомата, позволяющий минимизировать комбинационную схему автомата.

C этой целью возьмем автомат, граф которого имеет 5 состояний (рисунок 5.1).

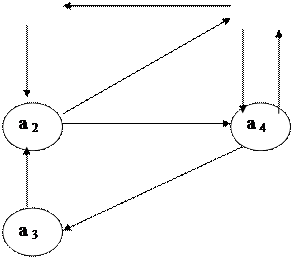Рисунок 5.1 – Автоматный граф

Алгоритм состоит из следующих шагов:

1.Построим матрицу, состоящую из всех различных пар номеров состояний, таких, что в автомате есть переходы для рассматриваемых пар.

Матрица строится таким образом, чтобы хотя бы один из элементов i-й строки содержался бы в какой-нибудь из предыдущих строк.

М =

Рисунок 5.2 – Матрица М

2.Закодируем состояния из первой строки матрицы следующим образом:

а₁ = 000; а₂ = 001. Кодирование будем иллюстрировать картой Карно.

Q 1 \ Q 2 Q 3

Рисунок 5.3 – Карта Карно после второго этапа

3.Вычеркнем из матрицы М первую строку, соответствующую закоди- рованным состояниям а₁ и а₂. Получим матрицу М '.

М ' =

Рисунок 5.4 – Матрица М '

4.В начальной строке матрицы М ' закодирован один элемент. Выбе- рем из первой строки М ' незакодированный элемент и обозначим его v. Т.е. v = 4.

5.Построим матрицу М ₄, выбрав из матрицы М ' строки содержащие 4. В ₄ - это множество элементов из матрицы М ', которые уже закодированы.В нашем случае закодирован только второй элемент.

М 4 =

Рисунок 5.5 – Матрица М ₄

6.Для каждого состояния найдем множество кодов, соседних с кодом рассматриваемого состояния и еще незанятых для кодирования состояний автомата: C'₂ = {101, 011}. Таким образом множество свободных кодов, которые могут использоваться для кодирования состояния 4: D'₄ = C'₂ = {101, 011} .

7.Для выбора кода вводим весовую функцию, характеризующую расстояние между кодами состояний, равное числу элементов памяти, изменяющих свое состояние при переходе:

W₁₀₁ = │101-001│ =1 ;

W₀₁₁ = │011-001│ =1 .

Выбираем а₄ = 101 и отмечаем на карте Карно.

Q 1 \ Q 2 Q 3

Рисунок 5.6 – Карта Карно после седьмого этапа

8.Вычеркнем из матрицы М ' 1-ую строку, тогда она будет иметь вид

М ' =

Рисунок 5.7 – Матрица М ' после восьмого этапа

9.Выберем из первой строки незакодированный элемент и обозначим его v = 5.

10.Построим матрицу М₅, выбрав из М ' строчки, содержащие 5.

М 5 =

Рисунок 5.7 – Матрица М ₅

Множество элементов из матрицы, которое уже закодировано В₅ = {2, 4, 1}.

11. Для каждого состояния из множества B₅ найдем соседние коды, еще неиспользуемые для кодирования: C'₂ = {011}, C'₄ = {100, 111}, C'₁ = {100, 010}. Таким образом множество свободных кодов, которое может использоваться для кодирования состоянии 5:

D'₅ ={011,100,111,010} .

12.Определим весовую функцию для каждого кода

W₀₁₁ =│011-001│+│011-101│+│011-101│+│011-000│= 1+2+2+2=7,

W₁₀₀ =│100-001│+│100-101│+│100-101│+│100-000│= 2+1+1+1=5,

W₁₁₁ =│111-001│+│111-101│+│111-101│+│111-000│= 2+1+1+3=7,

W₀₁₀ =│010-001│+│010-101│+│010-101│+│010-000│= 2+3+3+1=9.

Таким образом W₁₀₀ = min {W₀₁₁, W₁₀₀, W₁₁₁, W₀₁₀}.

Q 1 \ Q 2 Q 3

Рисунок 5.8 – Карта Карно после двенадцатого этапа

При расчете весовых функций учитывались только те состояния, с которыми связано состояние 5 (смотри граф переходов). Состояние 4 учи- тывалось дважды, так как они связаны двумя дугами .

13.Вычеркнем из матрицы М' первую строку и построим новую ма- трицу. В новую матрицу не входят также строки, где состояния уже за- кодированы.

М ' =

Рисунок 5.9 – Матрица М ' после трнадцатого этапа

14.Выберем из первой строки незакодированный элемент v = 3.

15.Построим матрицу М₃, выбрав из М ' строки, содержащие 3.

М 3 =

Рисунок 5.10 – Матрица М ₃

16.Множество элементов, которые уже закодированы В₃ = {2,4}.

17.Найдем соседние коды для каждого состояния:

С'₂ = { 011 }, C'₄ = { 111 }.

Таким образом множество свободных кодов, которые могут использо- ваться для кодирования состояния 3: D'₃ = {011, 111 }.

18.С помощью весовой функции выбираем код для рассматриваемого состояния:

W₀₁₁ =│011-001│+│011-101│=1+2=3,

W₁₁₁ =│111-001│+│111-101│=2+1=3.

Выбираем а₃ = 011 и отмечаем на карте Карно.

Q 1 \ Q 2 Q 3

Рисунок 5.8 – Карта Карно после восемнадцатого этапа

Таким образом состояния автомата закодированы.

Отметим, что если D¹_j = 0, то строим новое множество D²_j которое пред- ставляет множество кодов, у которых кодовое расстояние будет равно 2.

Если и D²_j = 0, то строим D³_j до тех пор пока Dⁿj = 0, где n = 1, 2, 3 ...

При каноническом методе структурного синтеза автоматов в качестве элементов памяти используются элементарные автоматы Мура с двумя устойчивыми состояниями. В качестве таких элементарных автоматов обычно используют D -, T -, RS -, JK - триггеры.

Очевидно, что число триггеров (элементов памяти) равно числу компонент вектора его состояний.

Удобно иметь специальную таблицу, в которой указано, какое зна- чение должен иметь сигнал возбуждения, чтобы соответствующий триггер перешел из состояния Q^s в Q^s+1 . Такие данные представлены в таблице 5.11.

Таблица 5.11 – Подграфы переходов триггеров

Qs ® Qs+1	D	T	R	S	J	K
0 0			¾			¾
0 1						¾
1 0					¾
1 1				¾	¾

Получим таблицу для определения функций возбуждения элементов памяти. Она получается на основе таблицы переходов, где вместо сос- тояний, в которые переходит автомат, записываем сигналы возбуждения триггеров, которые приведут триггер в нужное состояние.

В качестве элементов памяти автомата будем использовать Т -триггеры. Таблица возбуждений (таблица 5.12), соответствующая таблице переходов 5.9, приведена ниже.

Таблица 5.12 – Таблица возбуждений

Состояния	Входные сигналы
Q 1 Q 2	х = 0	х = 1
0 0	0 1	0 0
0 1	0 0	0 1
1 0	1 0	0 1
	Т 1 Т 2	Т 1 Т 2

Полученная таблица может быть интерпретирована как таблица

истинности. Поэтому, используя карты Карно, получим Т₁ и Т₂.

Таблица 5.13 – Карта Карно для Т ₁

х \ Q 1Q 2
			-
			-

T ₁ = Q ₁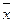

Таблица 5.14 – Карта Карно для Т ₂

х \ Q 1Q 2
			-
			-

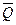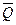T ₂ = Q ₂ x Ú Q ₁ x Ú _{1 2}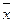

Получение булевых функций выходов проще и может быть сделано непосредственно по таблице выходов автомата. Уравнения булевых функций выходов автомата зависят от типа используемых элементов памяти, а зависят только от их количества.

Таблица 5.15 – Таблица выходов

Состояния	Входные сигналы
Q 1 Q 2	х = 0	х = 1
0 0	0 0	1 0
0 1	0 1	1 1
1 0	0 0	0 1

Таблица 5.16 – Карта Карно для у ₁

х \ Q 1Q 2
			-
			-

у ₁ = 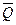₁ х

Таблица 5.17 – Карта Карно для у ₂

х \ Q 1Q 2
			-
			-

у ₂ = Q ₂ Ú Q ₁ х

Если синтезируемый автомат является автоматом Мура, то постро- ение булевых функций осуществляется также.

4.3 Задания выполняемые до лабораторного занятия.

Переведите номер по списку в двоичную систему счисления и запи- шите младшие четыре бита его в виде слова а ₁ а ₂ а ₃ а ₄.

1.Получите автоматный граф для цифровых автоматов Мура и Мили, на вход каждого из которых поступают двоичные данные в последова- тельной форме, синхронизируемые тактовыми импульсами. На выходе сиг- нал появляется только тогда, когда на вход подается последовательность бит а ₁ а ₂ а ₃ а ₄.

2.Получите автоматный граф для цифровых автоматов Мура и Мили

с наложением и без наложения входных стгналов

3.Реализуйте автоматы Мура и автоматы Мили, автоматные графы для которых получены в задании 2. Выбор элементов памяти (триггеров) осу- ществите следующим образом. Если два младших бита а₃ а₄ последова- тельности а₁ а₂ а₃ а₄ равны 00 – RS - триггер, 01 – JK - триггер, 10 – D - триггер, 11 – T - триггер.

4.4 Порядок выполнения работы

1.Соберите схемы автоматов Мура и Мили, которые получены в результате выполнения задания (пункт 2). Отладку и контроль правильности функционирования автоматов произвести по временным диаграммам, подавая на их вход все возможные комбинации входных сигналов. Тактирующие сигналы подавать с отдельного генератора одиночных импульсов.

2.Проверить правильность функционирования автоматов, разра- ботанных в соответствии с заданием для домашней подготовки (пункт 2).

3.Автоматы синтезировать как для последовательности с наложением входных сигналов, так и без наложения.

4.5 Содержание отчета

Отчет должен содержать краткие теоретические сведения, необхо-димые для выполнения заданий, автоматные графы, полученные в соответствии с заданием, процедуры минимизации числа состояний и их рационального кодирования. Схемы цифровых автоматов, результаты их экспериментального исследования с помощью временных диаграмм, а также выводы по работе.

4.6 Контрольные вопросы

1.Опишите процедуру минимизации числа состояний автомата.

2.Покажите эффективность рационального кодирования состояний.

3.В чем принципиальное отличие автоматов Мура и Мили?

4.Объясните уравнения, описывающие работу синхронных автоматов

Мура и Мили.

5.Назовите этапы при проектировании синхронных цифровых авто-

матов.

РЕКОМЕНДОВАННАЯ ЛИТЕРАТУРА

1. К.Г.Самофалов и др. Прикладная теория цифровых автоматов. – Киев: Вища школа, 1987.

2. Д.А.Поспелов. Логические методы анализа и синтеза схем. – М.: Энергия, 1974.

3. Г.Хоуп. Проектирование цифровых вычислительных устройств на интегральных схемах. – М.: Мир, 1984.

4. Б.Голдсуорт. Проектирование цифровых вычислительных устройств. – М.: Машиностроение, 1985.

5. С.И.Баранов. Синтез микропрограммных автоматов. – Л.: Энергия, 1974.