Или суммируя вероятности выделения горных пород по комплексу признаков по формуле полной вероятности.

Лабораторная работа №4.

Вычисление достоверности модели классификации горных пород

В зависимости от масштаба исследований роль физических параметров при создании легенды может быть различной. В тех случаях, когда проведенное разделение на классы геологическими методами удовлетворяет требованиям масштаба съемки, роль физических параметров состоит лишь в характеристике выделенных классов горных пород соответствующими статистическими оценками. Когда же такое расчленение является грубым, и для геологической съемки требуются более дробные классы, приходится прибегать к использованию дополнительных признаков. Такими признаками могут оказаться, в частности, физические и геохимические свойства горных пород.

Пусть имеется m горных пород и следовательно выдвигается m гипотез

P(H₁) P(H₂)… P(H_m) SP(H)=1 о том, что в некоторых точках пространства присутствует одна из горных пород. Горные породы изучаются комплексом признаков X₁ X₂ …X_k

i\j				...	m
				...
				...
				...
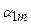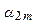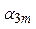...	...	...	...	aij	...
m				...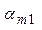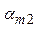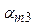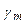

Здесь по строкам i выписаны ошибки первого рода, а по столбцам j ошибки второго рода.

Надежность выделения i-ой горной породы по признаку X на фоне всех других пород j вычисляется по формуле:

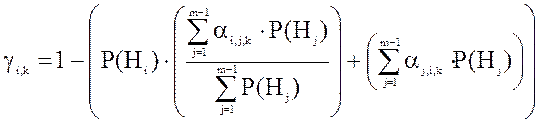; j¹i (1.10.2)

где: a_ik - ошибка первого рода при выделении породы i на фоне породы j;

a_ji- ошибка второго рода.

Надежность выделения горной породы i по комплексу признаков X_k (k= 1,2,... К) может быть найдена согласно теореме сложения вероятностей (появления совместных событий). Действительно, возможность разделения пород двух классов по одному признаку не исключает возможности их разделения по другим.

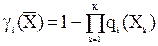(1.10.3)

где: q_i(X_k) = 1-g_i(X_k).

Достоверность классификации пород по каждому признаку Xk определяется по теореме о полной вероятности, где в качестве априорных вероятностей гипотез Р (Нi) выступают вероятности встречи породы i в исследуемом районе.

(1.10.4)

Надежность классификации по комплексу признаков можно вычислить как вероятность суммы событий (выделения пород по каждому признаку)

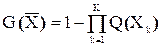(1.10.5)

где: Q(X_k) = 1 - G(X_k)

или суммируя вероятности выделения горных пород по комплексу признаков по формуле полной вероятности.

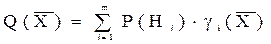(1.10.6)

По максимуму 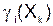или 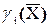определяется маркирующая порода, а по максимуму G(X_k) маркирующий признак X_k для всей легенды, а для породы i по max g_i(X_k) . Рассмотренные теоретические основы анализа свойств горных пород легенды документации позволяют решать и другие вопросы, в частности, выбор рационального комплекса признаков и подбор рационального метода преобразования признаков, которые реализованы в компьютерной системе анализа информации.

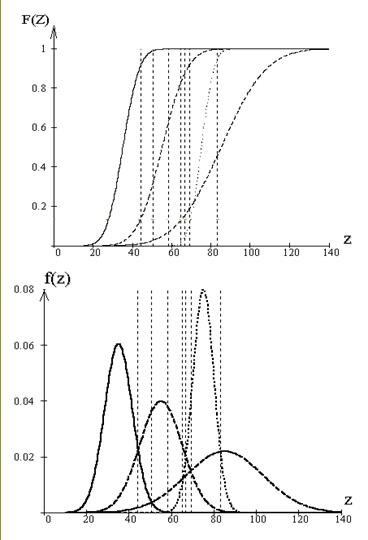
Пусть каждая горная порода характеризуется признаками Z,T. Задача вычислить достоверность легенды документации горных пород, т.е. посчитать вероятность того, что, используя эти признаки, можем разделить горную породу на классы которые отражены в легенде. К каждой разновидности горной породы по каждому признаку строятся свои интегральные и дифференциальные функции распределения. Пусть имеются четыре разновидности горных пород с заранее заданными математическими ожиданиями, среднеквадратическими отклонениями и априорными вероятностями их встречи

р(х₁)=0,2; p(x₂)=0,4; p(x₃)=0,3; р(х₄)=0,1.

Построим интегральную и дифференциальную функции распределения по первому признаку.