Основы проектирования на плис 1 страница
Учебное пособие
Омск, 2016
УДК 004.083
Рецензенты: д.т.н., профессор В.И.Потапов,
д.т.н., профессор В.П.Горелов
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
В настоящее время программируемые логические интегральные схемы (ПЛИС) являются одним из перспективных направлений развития современной микроэлектроники. Это объясняется следующими факторами.
1. Микропроцессорные техника и технологии привели к направлению развития вычислительной техники и ее приложений, включая мультимедийные приложения, IP - технологии, Интернет и связанные с ними достижения в области связи и дистанционных взаимодействий. В этой области не столь существенны производительность, помехоустойчивость и безотказность работы оборудования. Здесь же по-другому решаются вопросы информационной безопасности и защиты информации, поскольку при использовании ПЛИС отпадают проблемы с дистанционными и групповыми атаками, что является бичом IP- технологий.
2. ПЛИС могут использоваться при тиражировании современных технических средств различного уровня, от бытовой техники до современных технических средств оперативного управления и контроля. Они могут обладать следующими положительными свойствами:
- независимость от импортных программных продуктов зарубежного производства, включая Windows, Apple, Cisco и прочие программно ориентированные корпорации, что позволяет защититься от внешних нежелательных воздействий и финансовых проблем, связанных с лицензированием и обновлениями программных продуктов;
- ограничения технического шпионажа или дистанционных нежелательных воздействий на оборудование и технологически процессы;
- новые возможности оперативного перепрограммирования, включая дополнительную защиту от внешних атак и модернизацию алгоритмов работы оборудования.
3. Разработка, изготовление и тиражирование ПЛИС являются новым толчком современных нанотехнологий и основой для развития техники будущего. При разработке и тиражировании ПЛИС используются последние достижения в области физики, математики, химии и их практических приложений.
4. Разрабатываются новые приемы программирования и альтернативных операционных систем. Они могут включаться в новые системы автоматизированного проектирования (САПР) и способствуют созданию новых систем программирования и проектирования, включая блочное и объектно - ориентированное программирование. Удобством такого подхода является то, что любой автор собственной системы программирования является независимым владельцем и правообладателем своей системы программирования, предназначенной для решения узкого круга задач. Это не исключает создания тиражируемых систем программирования, которые могут являться объектами интеллектуальной собственности, следовательно, являются объектом коммерциализации.
5. Инженер - разработчик, имеющий в своем арсенале современные ПЛИС, обладающие огромными ресурсами по производительности, объему памяти и возможностями конфигурирования, получает существенные преимущества для создания, модернизации и тиражирования современных систем автоматизации, управления и комплексирования в множестве прикладных задач современных цифровых технологий.
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПЛИС
В этот раздел входят основные сведения из следующих направлений технической кибернетики:
- булева алгебра и исчисление высказываний;
- теория конечных автоматов;
- конечные динамические системы и машины Тьюринга;
- обучающиеся системы и искусственный интеллект.
Множество задач, входящих в эти разделы, слишком объемно, но авторы надеются, что означенные направления послужат толчком для дальнейшего самообразования и послужат основой для дальнейшего поиска в сети Интернет. Помните, что для корректной работы в любом направлении нужно умение корректно ставить задачи: на 70 – 80% это обеспечивает решение задачи. В ссылочных материалах приводятся некоторые данные об Интернет – ссылках по рассматриваемым проблемам.
1.1. Основы булевой алгебры и ее приложений
Несмотря на то, что основы этого направления были заложены еще в Древней Греции, принято считать, что его основоположником являлся Джордж Буль, преподаватель одного из колледжей Великобритании. В основе его теории лежала алгебра множеств, в то время уже достаточно разработанная, поэтому булева алгебра может считаться одним из ответвлений алгебры множеств.
В основе булевой алгебры лежит понятие двоичного аргумента - переменной, которая может принимать одно из двух значений: ноль или единица (0 или 1). В терминах Древней Греции это ассоциируется с понятиями «истина» (true) или «ложь» (false), что и было основой для раздела философии под названием «логика».
С исторической точки зрения, интерес к этому направлению появился во второй половине ХХ века при изобретении первых компьютеров. В их основе лежали электромагнитные реле, состоящие из катушки с сердечником и подвижным якорем, к которому механически присоединены контактные группы. При подаче напряжения на обмотку якорь притягивается к сердечнику, и при этом часть контактов или размыкается, или замыкается. Это послужило основой для развития современной цифровой техники.Использование принципа двоичной логики послужило толчком для современной цивилизации. Не исключено, что впоследствии будет переход на так называемую нечеткую логику, более приближенную к деятельности живых организмов. Тем не менее, алгоритмы нечеткой логики можно моделировать и на ПЛИС.
Булева функция оперирует с конечным множеством из каргументов. При этом, если каждый из аргументов принимает одно из двух значений, 0 или 1, возникает область определения, состоящая из конечного числа точек. Их количество оценивается как 2К, где К – количество аргументов.Обычно эту область называют пространством определения, а в булевой алгебре ассоциируют его с к– мерным кубом. В нем вершины определяют область определения, ребра имеют единичную длину, а координаты являются двоичными кодами этих вершин. При этом 0 – мерный куб представляет собой единственную точку с координатой 0, 1 – мерный куб – это отрезок единичной длины с координатами (0,1), двумерный куб – это квадрат с четырьмя координатами , трехмерный - это обычный куб в смысле Эвклида и т.д. Кубы большей мерности наглядно не воспринимаются (хотя алгоритм изображения кубов мерности 4 и выше можно записать в виде простого правила: для представления куба мерности к + 1 достаточно изобразить два к – мерных куба и соединить соответствующие вершины одномерными ребрами. Попробуйте изобразить эти кубы: после этого вы поймете технологии 4D).
ВариантыК- мерных кубов приведены на рис. 1.1.Здесь варианты а, б,в,г соответствуют нуль - одно - двух и трехмерным вариантам кубов.
Рисунок 1.1. - Варианты К - мерных кубов
Четырехмерный вариант куба не показан (хотя он освоен в технологиях типа 4D и их преемников). Остальные вариации пока считаются абстракцией, но это пока!
Вариантов задания булевых функций может быть несколько. Основными среди них можно считать табличный, алгебраический и графо - аналитический.
При табличном методе строится двумерная таблица, включающая столбцы с вариантами значений аргументов, столбцы с вариантами функций и строки со вариантами значений полученных функций.
Приведем таблицу булевых функций одного аргумента. Всего таких функций может быть 4. Их описание и функции приведены на рис.1.2. Как видно из рисунка, всего функций одного аргумента четыре. Из них две вырожденные и являются константами. Первая константа - 0: она сохраняет свое значение независимо от значения аргумента. Вторая константа, константа 1, сохраняет свое значение, но с другим знаком. Это второстепенные функции, не представляющие интереса для математики.
| Х | Обозначение | Наименование | ||
| Y1 | Константа 0 | |||
| Y2 | Х | Повторение Х | ||
| Y3 | /Х | Инверсия Х | ||
| Y4 | Константа 1 |
Рис. 1.2. - Булевы функции одного аргумента
Вторая функция из таблицы повторяет значения аргумента. Она так и называется - повторение. Практического значения не имеет.
Наконец, функция, третья в приведенной таблице и принимающая значения, противоположные значениям аргумента. Она называется инверсия и входит в основной ряд фундаментальных булевых функций.
Булевы функции двух аргументов являются основополагающими для всей цифровой техники и современных приложений. Именно на функциях двух аргументов основаны все современные цифровые технологии и их многочисленные приложения.
Приведем развернутую таблицу булевых функций двух аргументов. Как следует из предыдущего, количество таких функций равно 16. Таблица функций и их описание приведены на рис. 1.3.
Булевы функции двух аргументов приведены на рис. 1.3. Среди них есть и функции одного аргумента. Это прежде всего константы Y0 = 0 и Y15 = 1. Кроме них, известны функции повторения Y3 = X2 и Y5 = X1, а также инверсии Y10 = \X1 и Y12 = \X2. Остальные функции нуждаются в дополнительных комментариях.
| Х1 | Обознач | Выраж | Наименование | ||||
| Х2 | |||||||
| Y0 | Y=0 | Х|X | Константа 0 | ||||
| Y1 | X1&X2 | X1X2 | Конъюнкция | ||||
| Y2 | Х2←Х1 | |X1X2 | Запрет по Х1 | ||||
| Y3 | X2 | X2 | Повторение Х2 | ||||
| Y4 | Х1←Х2 | X1|X2 | Запрет по Х2 | ||||
| Y5 | X1 | X1 | Повторение Х1 | ||||
| Y6 | X1ѲX2 | X1|X2+|X1X2 | Неравнозначность | ||||
| Y7 | X1+X2 | X1+X2 | Дизъюнкция | ||||
| Y8 | Х1\ Х2 | |X1|X2 | Штрих Шеффера | ||||
| Y9 | Х1≈Х2 | X1X2+|X1|X2 | Равнозначность | ||||
| Y10 | │Х1 | |X1 | Инверсия Х1 | ||||
| Y11 | Х2→Х1 | |X1+X2 | Имплик. от Х2 к Х1 | ||||
| Y12 | │Х2 | |X2 | Инверсия Х2 | ||||
| Y13 | Х1→Х2 | X1+|X2 | Имплик. от Х1 к Х2 | ||||
| Y14 | X1↓X2 | |X1|X2 | Стрелка Пирса | ||||
| Y15 | Y=1 | X + |X | Константа 1 |
Рисунок 1.3 - Булевы функции двух аргументов
Функция Y1 принимает значение 1 только в случае, когда оба аргумента равны 1. Она называется логическое умножение или конъюнкция и имеет большое прикладное значение. Ее также называют функция И.
Функция Y7 равна 1, если хотя бы один из аргументов принимает значение 1. Это логическое сложение, или дизъюнкция, а также функция ИЛИ.
Функция Y9 принимает значение 1, если оба аргумента одинаковы, или1, или 0. Это равнозначность.
Обратная равнозначности функция – неравнозначность, Y6. или исключающее ИЛИ. Функция также носит название сложение по модулю 2 и имеет большое прикладное значение в цифровых технологиях.
Очень важное значение имеют функции Y8 и Y14. Первая, штрих Шеффера, принимает значение 1 только в случае, если оба аргумента равны 0, и называется еще функцией И – НЕ; вторая, равная 0 только при обоих аргументах, равных 1, носит название стрелка Пирса, но чаще называется ИЛИ – НЕ. При проектировании ПЛИС они имеют первостепенное значение (и не только в ПЛИС: микропроцессоры, системы электронной памяти и цифрового управления в качестве базовых элементов используют триггеры, о которых будет сказано впоследствии. Они строятся на схемах И - НЕ и ИЛИ - НЕ).
Перечисленные выше функции относятся к классу симметричных: они не меняют значения при перемене значений аргументов (например, Х1&Х2 = Х2&Х1; Х1≈Х2 = Х2≈Х1 и т.д.). Четыре оставшиеся функции являются несимметричными. Рассмотрим, в частности, функцию Y2. Если Х1 равен 1, Y = 0, при Х1=0 Y повторяет значения Х2. Функция носит название запрет по Х1. Аналогично Y4 является запретом по Х2.
Функции Y11 и Y13 являются взаимообратными относительно Y4 и Y2 соответственно. Они называются импликацией и используются сравнительно редко.
В булевой алгебре важной задачей является отыскание возможности выражения функций через другие. Это позволяет сокращать запись логических выражений и в конечном итоге упростить аппаратную реализацию (следовательно, повысить надежность технических систем).
Обратим внимание, что, если между функциями Y7 и Y8 провести горизонтальную линию, то функции, размещенные симметрично относительно нее, являются взаимно инверсными. Например, Y0 = \Y15 ; Y1 = \Y14 и т.д.
В булевой алгебре вводится понятие функционально полная система: такой набор, с помощью которого можно описать любую функцию любого числа аргументов. Доказано, что для такого набора достаточно не больше четырех функций. Наиболее распространен набор из трех функций: И, ИЛИ, НЕ. Его особенностью является прежде всего то, что он вытекает непосредственно из алгебры множеств, предшественницы алгебры логики. Алгебра, основанная на этой системе функций, называется исчислением высказываний. Она основана на системе аксиом, т.е., правил, не доказываемых в рамках этой алгебры и являющихся основой для дальнейших преобразований и доказательства теорем.
Кроме того, в исчислении высказываний справедлив принцип двойственности: любое алгебраическое выражение выражает ту же функцию, если в нем заменить операции умножения на сложение и наоборот, нули на единицы и наоборот.
Таблица аксиом исчисления высказываний приведена на рис. 3. Она включает две группы аксиом, относительно логического умножения & и логического сложения +. Для упрощения записи знаки &, как в обычной алгебре, опускаются.
Часть аксиом несамостоятельна, т.е. может доказываться на основе других. Они в совокупности представляют повторение алгебры множеств и в дальнейшем будут использоваться при эквивалентных алгебраических преобразованиях.
| & | Наименование | + |
| Х1Х2 = Х2Х1 | коммутативность | Х1+Х2 = Х2+Х1 |
| Х1(Х2Х3) = (Х1Х2)Х | ассоциативность | (Х1+Х2) +Х3 = Х1+(Х2+Х3) |
| Х1(Х2+Х3)=Х1Х2 + Х1Х3 | дистрибутивность | Х1+(Х2Х3) = (Х1+Х2)(Х1+Х3) |
| ХХХ……Х=Х | идемпотентность | Х+Х+Х+…..+Х=Х |
| //Х=Х | ||
| Х&/Х= 0 | Х+/Х=1 | |
| Х&1=Х | Х+0=Х | |
| Х&0=0 | Х+1=1 | |
| /(Х1Х2) = /Х1+/Х2 | Де Моргана | /(Х1+Х2) = /Х1/Х2 |
Рисунок 1.4 – Аксиомы булевой алгебры
Возможны и другие функционально полные системы. В частности, функции Y8 (И-НЕ) и Y14 (ИЛИ-НЕ) каждая представляют функционально полную систему, но получаемые при этом выражения намного длиннее, чем при использовании классического исчисления высказываний. Кроме того, для исчисления высказываний разработан мощный математический аппарат, используемый в ряде программных продуктов, в том числе в САПР.
Совершенные нормальные формы
Являются как доказательством возможности описания любой булевой функции, так и основанием для их упрощения.
Существуют две основных формы такого описания: совершенная дизъюнктивная нормальная форма (сокращенно СДНФ) и совершенная конъюнктивная нормальная форма, или СКНФ. Более предпочтительна СДНФ, на которой мы и остановимся.
Дальнейшее описание лучше делать на конкретном примере. Опишем произвольную функцию трех аргументов с помощью таблицы, приведенной на рис. 1.5.
| Х3 | Х2 | Х1 | Y |
Рисунок 1.5. – Пример функции трех аргументов
Введем теперь определение конституента единицы. Это произведение всех аргументов, причем значению 1 аргумента в записи произведения будет сам аргумент, а значению 0 – его инверсия. Так, вторая строка таблицы с координатами 001 соответствует конституенте /Х3/Х2Х1. В соответствии с аксиомой коммутативности чаще пишут аргументы в порядке возрастания индексов, т.е. Х1/Х2/Х3.
СДНФ представляет собой дизъюнкцию всех конституент, для которых описываемая функция равна 1. В данном примере в описание входят 5 конституент, а общая запись принимает вид:
Y = Х1/Х2/Х3 + Х1Х2/Х3 + /Х1/Х2Х3 + Х1/Х2Х3 + Х1Х2Х3
Чтобы доказать равенство левой и правой частей, достаточно подставить в них все возможные точки из области определения функции. При этом используется следующее свойство конституенты: она равна 1 только для одного набора значений аргументов, называемого соответствующим. Нетрудно убедиться, что при такой записи СДНФ левая и правая части совпадают.
СКНФ булевой функции проще получить из СДНФ, используя принцип двойственности: достаточно получить СДНФ, после чего заменить умножения сложениями и наоборот. Так, для приведенной выше функции СКНФ будет иметь вид:
Y = (Х1+/Х2+/Х3)(Х1+Х2+/Х3)(/Х1+/Х2+Х3)(Х1+Х2+Х3).
Эта форма по некоторым причинам не нашла особого применения.
Попробуем провести упрощение приведенной СДНФ, используя алгебраические преобразования. Объединим первый член со вторым, а третий – с четвертым:
Y= Х1/Х3(/Х2+Х2) + /Х2Х3(/Х1+Х1) + Х1Х2Х3.
Выражения в скобках равны 1, поэтому окончательно:
Y = Х1/Х3 + /Х2Х3 + Х1Х2Х3.
Мы получили сокращенную ДНФ, но она не обязательно минимальна, так как при алгебраическом сокращении снижаются возможности манипулирования, так как сокращенные произведения могут не участвовать в дальнейших преобразованиях. Известно, что для получения наиболее короткой записи (т.е. для минимизации) необходимы неалгебраические методы. Некоторые мы и рассмотрим.
Методы минимизации булевых функций
Для описания методов минимизации необходимо ввести понятие накрытия. Пусть заданы две функции, Y1 и Y2. При произвольном наборе аргументов обе функции принимают одно из двух значений, 0 или 1. При этом, если значения функций совпадают и равны 1, говорят, что функция Y2 накрывает своей единицей функцию Y1. Для минимизации необходимо и достаточно, чтобы единицы минимальной функции накрывали все единицы исходной. При этом допускается неоднократное накрытие некоторых единиц, что и составляет «изюминку» неалгебраических методов.
Следует помнить, что при минимизации теряется взаимно однозначное соответствие: одной функции может соответствовать две и больше минимальных.
Геометрический метод минимизации
В основе геометрического метода лежит представление области определения булевой функции как вершин К – мерного куба. Наиболее наглядно это выглядит для К=3, т.е. для куба в классическом представлении.
Рисунок 1.6. – Разметка трехмерного куба (а) и нанесение единиц (б)
На рис. 1.6,а показана разметка трехмерного куба с координатами вершин. Дадим дополнительные объяснения модели. Каждая вершина трехмерного куба имеет три координаты, Х1, Х2 и Х3. Совокупность этих координат сопоставляется с трехбуквенным произведением, причем если аргумент в этой точке равен 1, соответствующий аргумент записывается без инверсии, если 0 – с инверсией. Так, точке А соответствует произведение /Х1/Х2/Х3; точке С – Х1Х2/Х3; точке Н - /Х1Х2Х3.
Любое ребро на кубе (а их всего 12) соединяет две смежные точки и соответствует двухбуквенному произведению, для которого две координаты неизменны. Например, ребру DH соответствует произведение /Х1Х2; ВС – Х1/Х3.
Грани на кубе (всего их 8) накрываются однобуквенными произведениями, соответствующими аргументам, не меняющимся на этой грани. Так, BFGC накрывается аргументом Х1, EHGF – Х3, HGFE – Х2.
Тогда алгоритм минимизации функции трех аргументов запишется в виде.
1. Размещаем единицы исходной функции в вершинах трехмерного куба.
2. Ищем на кубе грани с единицами во всех вершинах и накрываем их однобуквенными произведениями.
3. Среди оставшихся не накрытыми единиц ищем ребра с единицами в вершинах и накрываем их двухбуквенными произведениями.
4. Оставшиеся одиночные единицы накрываются трехбуквенными произведениями.
Применим алгоритм к приведенной в качестве примера функции. Размещаем на кубе единицы и помечаем их, как показано на рис. 1.6, б (п. 1 алгоритма). Ищем и находим грань с единицами: это ABED. Накрываем грань однобуквенным произведением Х1. Оставшуюся не накрытой единицу С объединяем с D и накрываем произведением /Х2Х3. Таким образом, окончательно Y = Х1 + /Х2Х3.
Как видим, для функции трех аргументов геометрический метод достаточно прост и эффективен. Наиболее сложным является вариант, когда для функции с 6 единицами нули размещены на главной диагонали. Таких вариантов 4. Рассмотрим один из них (см. рис. 1.6 в). Граней с единицами здесь нет, т.е. отсутствуют однобуквенные произведения. Зато существует два варианта минимизации с использованием граней. Первый соответствует набору ребер, помеченных одним штрихом, второй – двумя. Легко можно получить эти варианты:
Y1 = |X2X3 + X1X2 + |X1|X3 ;
Y2 = |X1|X2 + X1C3 + X2|X3 .
Отсюда видно, что при минимизации теряется взаимно однозначное соответствие.
Прежде, чем переходить к интерпретации геометрического метода для функций с числом аргументов больше 3, приведем алгоритм построения куба мерности К+1. Для этого изображаются два куба мерности К, после чего ребрами соединяются все их соответствующие вершины. В качестве примера на рис. 1.7 приведено построение четырехмерного куба. Несмотря на внешнюю простоту построения, трудно представить такой куб.
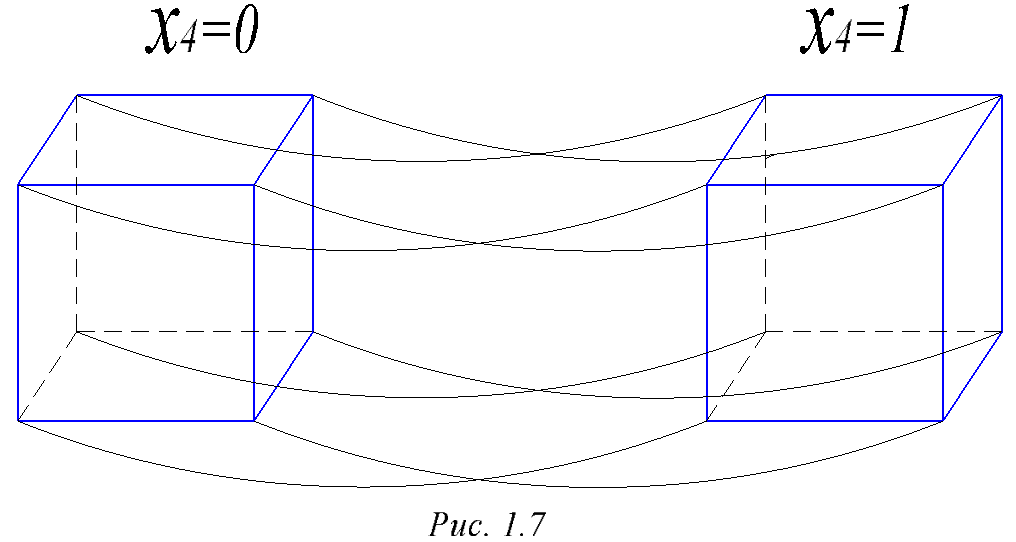
Рисунок 1.7.- Графическое представление четырехмерного куба
Обобщенный алгоритм минимизации функции К аргументов записывается в следующей форме.
1. На вершины К – мерного куба наносятся единицы исходной функции.
2. На К – мерном кубе ищутся кубы мерности К-1 с единичными вершинами. Они накрываются однобуквенными произведениями.
3. Среди оставшихся не накрытыми ищутся единицы, лежащие в вершинах кубов мерности К-2 и накрываются дкухбуквенными произведениями.
……………………………………………………………………………..
К+1 Одиночные единицы накрываются К – буквенными произведениями .
Геометрический метод, хотя и претендует на наглядность, трудно формализуется.
Метод Карно
Метод хорош для функций 3 и 4 аргументов. Классическим считается четырехмерный вариант. Для реализации метода строится специальная таблица – карта Карно. Она приведена на рис. 1.8, а.
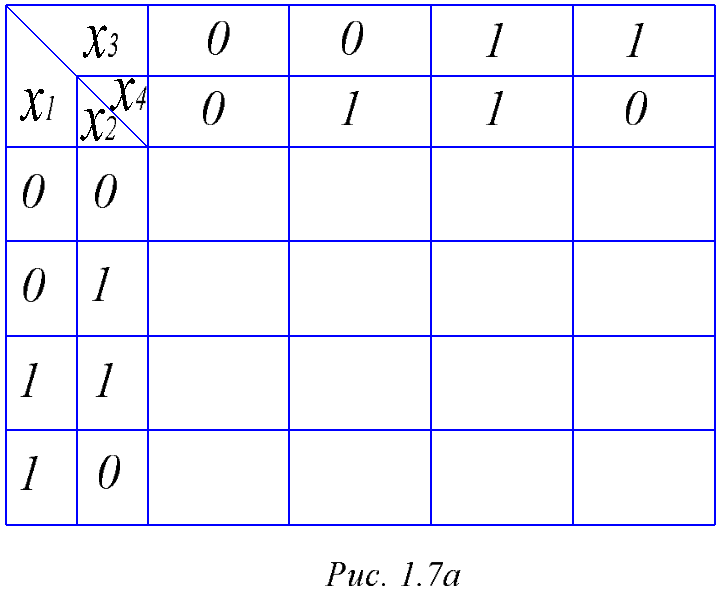
Рисунок 1.8. – Карта Карно
Собственно карта – это квадратная таблица, отделенная жирными линиями. Дополнительные поля образуют сетку координат. Координаты записаны таким образом, что основное поле находится на поверхности воображаемого тора. При этом на поверхности тора соседними являются первая и последняя строка таблицы и ее первый и последний столбцы.
Упрощенное изображение карты Карно показано на рис. 1.8, б. Здесь линиями показаны строки (столбцы), для которых соответствующие аргументы равны 1.
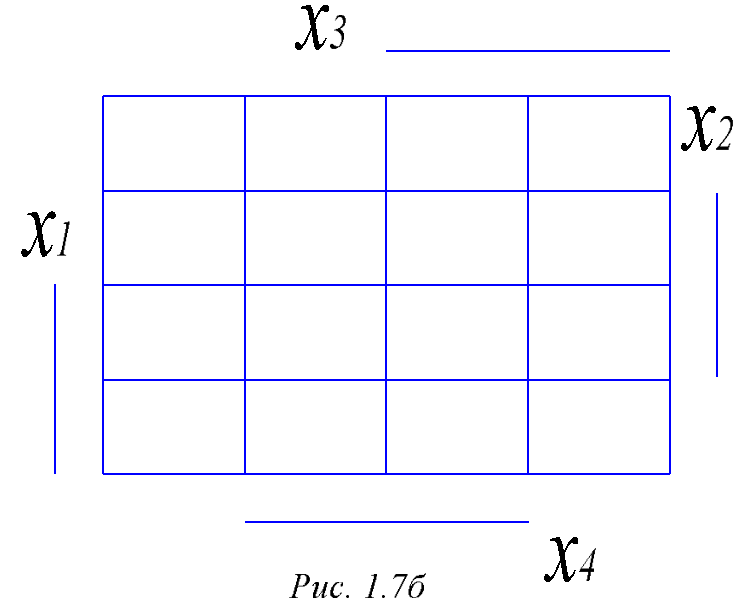
На карте Карно своеобразное понятие соседства. Соседними являются первая и последняя строка и первый и последний столбцы, так как таблица размещена на торе.
После такой преамбулы можно сформулировать собственно алгоритм минимизации. Для этого воспользуемся примером функции четырех аргументов, заданной в виде сокращенной ДНФ:
Y = /Х1Х2Х4 + Х1/Х2Х3 + Х1/Х2Х4 + Х1Х2/Х4 +/Х1/Х2Х4 +/Х2/Х3Х4
Необходимо привести эту функцию к СДНФ, для чего воспользуемся следующим приемом: для привлечения недостающего аргумента домножим каждую сокращенную форму на сумму недостающего аргумента и его инверсии. В частности, первый член предыдущего выражения преобразуется к виду:
/Х1Х2Х4 = /Х1Х2Х4(Х3+/Х3) = /Х1Х2Х3Х4 + /Х1Х2/Х3Х4
Продолжая эту процедуру для оставшихся членов сокращенной формы, в итоге получаем СДНФ:
Y = |X1X2X3X4 + |X1X2|X3X4 + X1|X2X3X4 + X1|X2X3|X4 + X1|X2|X3X4 + X1X2X3|X4 + X1X2|X3|X4 + |X1|X2X3X4 + |X1|X2|X3X4
Размещаем теперь конституенты на карту Карно (см. рис.1.9).
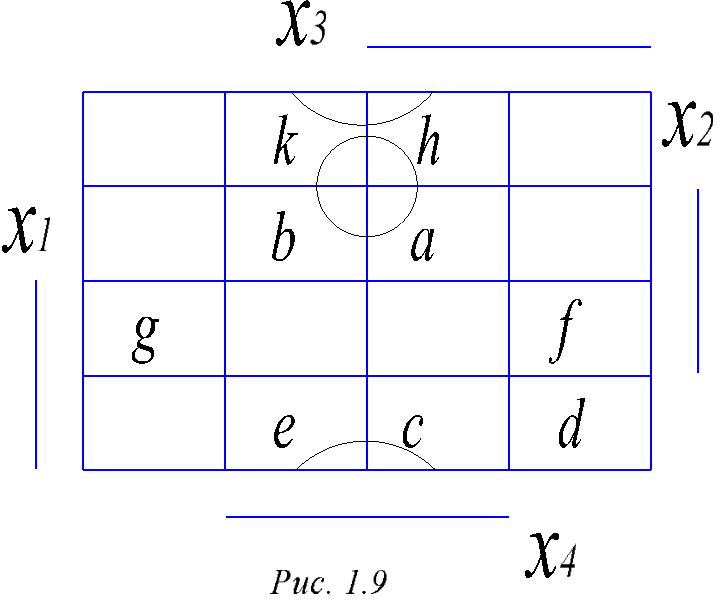
Сформулируем теперь сам алгоритм.
1. Наносим единицы функции на карту Карно
2. Ищем на карте группы из 8 соседних единиц. Это или две соседние строки с единицами, или два соседних столбца. Они накрываются однобуквенными произведениями, для которых соответствующий аргумент неизменен.
3. Из оставшихся не накрытыми единиц ищем группы из четырех соседних. Это или строка, или столбец, или квадрат на торе. Они заменяются двухбуквенными произведениями.
4. Из оставшихся не накрытыми ищем группы из двух соседних единиц и накрываем их трехбуквенными произведениями.
5. Одиночные единицы накрываются четырехбуквенными произведениями.
Применим этот алгоритм к нашему примеру (см.рис. 1.9). Групп из 8 элементов не обнаруживается. Зато есть две группы из 4 элементов: abkh (соответствует произведению \Х1Х4) и khec (произведение /Х2Х4). Оставшиеся единицы накрываются трехбуквенными произведениями: fd (Х1Х3/Х4) и fg (X1X3|X4). Таким образом минимальная ДНФ имеет вид:
Y = |X1X4 + |X2X4 + X1X3|X4 + X1X3|X4.
Возможен и второй вариант минимальной ДНФ, если выбрать другой вариант двухбуквенных накрытий: cd и fg. Тогда получим:
Y = |X1X4 + |X2X4 + X1X3|X4 + Х1/Х2Х3.
С помощью карт Карно возможна минимизация и функций трех аргументов. Карта в этом случае приобретает вид, показанный на рис. 1.10.
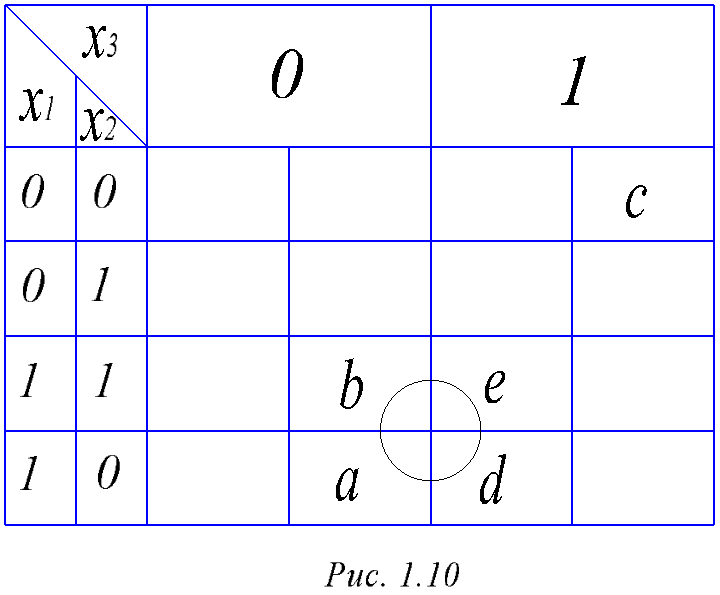
Основное поле , обведенное жирной линией, размещается на поверхности цилиндра, на которой соседними являются первая и последняя строка. Алгоритм минимизации такой же, только пропущен п.2. В качестве примера рассмотрим ту же функцию, что и при рассмотрении геометрического метода минимизации. Размещение единиц показано на том же рисунке с теми же обозначениями. Ищем и находим группу из 4 соседних единиц: beda. Накрываем ее однобуквенным произведением Х1. Оставшуюся ненакрытой единицу с объединяем с d, что соответствует двухбуквенному произведению /Х2Х3. Итак, Y = X1 + |X2Х3, что совпадает с результатами минимизации геометрическим методом.
К сожалению, метод Карно ограничен рамками нашего восприятия. Уже для К=5 трудно представить четырехмерную поверхность и тем более отношения соседства на ней.
Метод Квайна
В отличие от предыдущих методов минимизации, метод Квайна позволяет минимизировать функции произвольного числа аргументов. Плата за это – излишняя громоздкость. С другой стороны, метод легче формализовать и следовательно автоматизировать.
