Наименьшая эрбрановская модель
Пусть  – логическая программа. Обозначим через
– логическая программа. Обозначим через  множество всех э-моделей программы
множество всех э-моделей программы  . Оно не пусто (см. упр. 3). Множество
. Оно не пусто (см. упр. 3). Множество  есть э-модель, называемая наименьшей э-моделью.
есть э-модель, называемая наименьшей э-моделью.
Предложение 2.  .
.
Пример 10. Эрбрановский базис 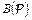 в примере 1 состоит из 18 атомов (найдите их). При этом в силу предложения 2 наименьшей э-моделью для
в примере 1 состоит из 18 атомов (найдите их). При этом в силу предложения 2 наименьшей э-моделью для  будет
будет  {ОТЕЦ (ИВАН, ПЁТР), ОТЕЦ (ПЁТР, СЕМЁН), ДЕДУШКА (ИВАН, СЕМЁН)} (заметим, что отличными от неё э-моделями являются, например:
{ОТЕЦ (ИВАН, ПЁТР), ОТЕЦ (ПЁТР, СЕМЁН), ДЕДУШКА (ИВАН, СЕМЁН)} (заметим, что отличными от неё э-моделями являются, например:  {ОТЕЦ (ИВАН, СЕМЁН)},
{ОТЕЦ (ИВАН, СЕМЁН)},  {ОТЕЦ (СЕМЁН, ИВАН), ДЕДУШКА (СЕМЁН, ПЁТР), ДЕДУШКА (ПЁТР, ИВАН)}).
{ОТЕЦ (СЕМЁН, ИВАН), ДЕДУШКА (СЕМЁН, ПЁТР), ДЕДУШКА (ПЁТР, ИВАН)}).
Множество  всех подмножеств эрбрановского базиса (т.е. множество всех э-интерпретаций программы
всех подмножеств эрбрановского базиса (т.е. множество всех э-интерпретаций программы  ) образует полную решётку [6]относительно частичного порядка, задаваемого теоретико-множественным включением
) образует полную решётку [6]относительно частичного порядка, задаваемого теоретико-множественным включением  .
.
Определим отображение  из решётки э-интерпретаций в себя. Пусть
из решётки э-интерпретаций в себя. Пусть 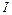 – э-интерпретация. Тогда
– э-интерпретация. Тогда  {
{  есть основной пример некоторого дизъюнкта из
есть основной пример некоторого дизъюнкта из  и
и  }
} 
Предложение 3. 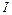 – э-модель для
– э-модель для  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Введём обозначения:  Ø,
Ø,  , если
, если  – непосредственно следующий ординал [3];
– непосредственно следующий ординал [3];  если
если  – предельный ординал.
– предельный ординал.
Скажем, что интерпретация 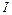 – наименьшая неподвижная точка отображения
– наименьшая неподвижная точка отображения  если
если 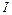 – неподвижная точка (т.е.
– неподвижная точка (т.е.  ) и для всех неподвижных точек
) и для всех неподвижных точек  отображения
отображения  имеем
имеем  Наименьшая неподвижная точка отображения
Наименьшая неподвижная точка отображения  обозначается
обозначается  . Аналогично определяется наибольшая неподвижная точка:
. Аналогично определяется наибольшая неподвижная точка: 
Теорема 2[7]. 
Пример 11. Наименьшая э-модель 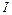 из примера 10 является, как легко проверить, неподвижной точкой отображения
из примера 10 является, как легко проверить, неподвижной точкой отображения  а по теореме 2 и наименьшей его неподвижной точкой.
а по теореме 2 и наименьшей его неподвижной точкой.
Пусть  – программа,
– программа, 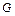 – цель
– цель  Ответной подстановкой для
Ответной подстановкой для 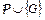 называется подстановка только для переменных из
называется подстановка только для переменных из  но не обязательно для всех. При этом все константы и функции из подстановки считаются уже встретившимися в
но не обязательно для всех. При этом все константы и функции из подстановки считаются уже встретившимися в 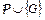 .
.
Корректная ответная подстановка для 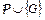 – это такая ответная подстановка
– это такая ответная подстановка  что универсальное замыкание формулы
что универсальное замыкание формулы  есть логическое следствие из
есть логическое следствие из 
Пример 12. Ответными подстановками в примере 1 могут быть:  и др. Не являются ответными, например, подстановки:
и др. Не являются ответными, например, подстановки:  Корректной ответной подстановкой является лишь подстановка
Корректной ответной подстановкой является лишь подстановка  .
.
Предложение 4. Пусть 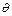 – ответная подстановка для
– ответная подстановка для 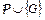 такая, что формула
такая, что формула  не содержит переменных. Следующие утверждения эквивалентны друг другу:
не содержит переменных. Следующие утверждения эквивалентны друг другу:
а) 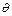 – корректная ответная подстановка,
– корректная ответная подстановка,
б)  истинно в любой э-модели для
истинно в любой э-модели для 
в)  истинно в наименьшей э-модели для
истинно в наименьшей э-модели для 
Упражнения:
12. Пусть  – непустое множество э-моделей для программы
– непустое множество э-моделей для программы 
Доказать, что  есть э-модель.
есть э-модель.
13. Почему  – непустое множество?
– непустое множество?
14. Пусть  – конечное множество дизъюнктов,
– конечное множество дизъюнктов,  – непустое множество э-моделей для
– непустое множество э-моделей для  Показать, что
Показать, что  не обязательно модель.
не обязательно модель.
15. Проверить, что множество всех э-интерпретаций для программы  является полной решёткой относительно теоретико-множественного отношения
является полной решёткой относительно теоретико-множественного отношения 
16. Пусть  – программа вида
– программа вида




Показать, что  где
где  , и поэтому
, и поэтому  .
.
17. Проверить, что:
а) если цель 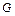 не содержит переменных (основной дизъюнкт), то единственной возможной ответной подстановкой является
не содержит переменных (основной дизъюнкт), то единственной возможной ответной подстановкой является 
б) предложение 4 в общем случае несправедливо, если не требовать условия отсутствия переменных в 
