Обеспечение точности измерений

3.1. Точным измерениям присущи отсутствие промахов и малость систематических и случайных погрешностей.

3.2. Промахи исключают из результатов измерений.

3.2.1. При однократных измерениях обнаружить промах не представляется возможным. Чтобы уменьшить вероятность получения промаха в результате измерений, необходимо повторить измерения 2–3 раза, а за результат измерений принять среднее арифметическое полученных отсчетов.

3.2.2. При многократных измерениях для обнаружения промахов используют статистические критерии [1]. Предварительно должно быть проверено, какому виду распределения соответствует распределение результатов измерений в соответствии с требованиями НТМ СЭВ 1–84. Для результатов измерений, распределенных нормально, наибольшее (наименьшее) значение X_i является промахом, если удовлетворяется неравенство [1]

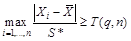, (1)

где	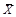– среднее арифметическое группы результатов измерений;
S*	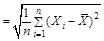– смещенное среднее квадратическое отклонение группы результатов измерений;
Т (q, n)	– квантиль распределения, соответствующий уровню значимости q и числу измерений n в группе (см. приложение 1);
n	– число измерений в группе.

3.3. Обнаруженные систематические погрешности должны быть устранены из результатов измерений путем введения поправок.

Неисключенные остатки систематических погрешностей, границы которых обозначены Q, оцениваются нестатистическими методами в соответствии с требованиями МИ 1552–86 и ГОСТ 8.207–76.

3.3.1. Постоянно возрастающую или постоянно убывающую систематическую погрешность можно обнаружить по одной группе результатов измерений посредством критерия Аббе (см. приложение 2) [3].

3.3.2. Не изменяющуюся в процессе измерений систематическую погрешность не представляется возможным обнаружить по одной группе многократных измерений.

При наличии двух или более групп результатов измерений физической величины одного и того же значения, полученных различными методами или средствами измерений, различными операторами либо отличающиеся условиями или методикой выполнения измерений, возникающую при этом неизменяющуюся систематическую погрешность или различия систематических погрешностей в группах можно обнаружить посредством нижеизложенных статистических критериев.

3.3.2.1. При наличии двух групп результатов измерений одной и той же физической величины, имеющих нормальное распределение с однородными ( 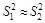) средними квадратическими отклонениями, неизменяющуюся систематическую погрешность или различия систематических погрешностей в группах можно обнаружить посредством критерия Стьюдента. Систематическая погрешность присутствует в одной из групп или они различны в группах, если выполняется неравенство

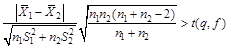, (2)

где 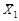,	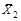– средние арифметические значения, соответственно, первой и второй групп результатов измерений;
S1, S2	– средние квадратические отклонения первой и второй групп, соответственно;
n1, n2	– число измерений в первой и второй группах, соответственно;
t (q, f)	– квантиль распределения Стьюдента, соответствующий уровню значимости q и числу степеней свободы f = n1 + n2 – 2.

Квантили распределения Стьюдента в зависимости от уровня значимости q и числа степеней свободы f представлены в приложении 3.

Примечание. Однородность средних квадратических отклонений проверяют посредством критериев, изложенных в пп. 3.4.2.4, 3.4.2.5.

3.3.2.2. Если средние квадратические отклонения не однородны, то вместо неравенства (4) используют неравенство

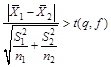, (3)

где f – число степеней свободы является наибольшим целым числом, не превосходящим

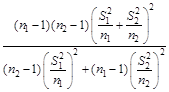. (4)

3.3.3. При нормальном распределении нескольких групп (L ³ 3) результатов измерений одной и той же физической величины для обнаружения систематической погрешности или различия систематических погрешностей в группах применяют критерий Фишера. Систематические погрешности различны в группах или присутствуют в одной из групп, если выполняется неравенство [1].

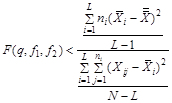, (5)

где , ,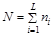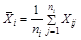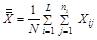
L	– число групп результатов измерений;
ni	– число измерений в i-й группе;
F (q, f1, f2)	– квантиль распределения Фишера, соответствующий уровню значимости q и числу результатов измерений в группах f1 = L – 1, f2 = N – L (см. приложение 4).

3.3.4. При неизвестном распределении результатов измерений групп для обнаружения систематической погрешности или различия систематических погрешностей в группах применяют статистический критерий Вилкоксона (см. приложение 5).

3.4. По значениям случайных погрешностей измерений могут оцениваться сходимость измерений (т. е. близость друг к другу результатов измерений, выполняемых в одинаковых условиях) и воспроизводимость измерений (т. е. близость друг к другу результатов измерений, выполненных в различное время, в разных местах, разными методами и средствами измерений, но приведенных к одним и тем же условиям – температура, давление, влажность и т. д.).

3.4.1. Сходимость группы результатов измерений характеризуют средним квадратическим отклонением результата группы или его доверительной случайной погрешностью.

3.4.2. Воспроизводимость нескольких групп результатов измерений характеризуют близостью результатов измерений групп и характеристик их случайных погрешностей.

3.4.2.1. При нормальном распределении результатов измерений для проверки близости (допустимости различия) результатов измерений групп следует пользоваться статистическими критериями, изложенными в пп. 3.3.1, 3.3.3.

3.4.2.2. Для проверки допустимости различия средних квадратических отклонений двух групп результатов измерений (близости средних квадратических отклонений) используют критерий Фишера, для числа групп более двух – критерий Бартлетта [5].

3.4.2.3. Различие средних квадратических отклонений S₁ и S₂ двух групп результатов измерений с числом измерений n₁ и n₂ допустимо, если выполняется неравенство

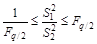. (6)

Значение критические значений F_q/2 в зависимости от числа степеней свободы f₁ = n₁ – 1 и f₂ = n₂ – 1 для уровней значимости 0,05 и 0,01 приведены в таблицах приложения 4.

3.4.2.4. Различие средних квадратических отклонений S₁, S₂,..., S_L групп результатов измерений допустимо, если выполняется неравенство

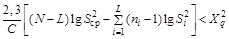, (7)

где, C	,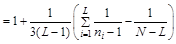
	,
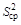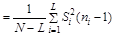N	,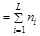
ni	– число результатов измерений в i-й группе;
X2 (q, f)	– квантиль распределения X2, соответствующий уровню значимости q и числу степеней свободы f = L – 1 (см. приложение 6).

3.4.2.5. При неизвестном распределении результатов измерений для проверки близости результатов измерений групп применяют статистический критерий Вилкоксона, а для проверки допустимости различия средних квадратических отклонений – критерий Сиджела-Тьюки (см. приложение 5).

3.5. Указание о том, на каких этапах оценивания погрешности измерений целесообразны указанные критерии и их влияние на последующий ход оценивания погрешностей, должно быть рекомендовано НТД, регламентирующими методы обработки результатов конкретных измерений.

3.6. Ввиду разнообразия причин, вызывающих систематические погрешности, невозможно во всех случаях дать исчерпывающие правила их исключения. В ряде случаев можно выполнить работы по выявлению и устранению этих погрешностей [7]:

при подготовке к выполнению измерений – это поверка применяемых СИ с целью определения действительного значения их погрешностей, предварительный анализ методической погрешности с целью введения поправок, фиксация измерений влияющих величин, поддержание стабильности условий измерений;

при выполнении измерений – это использование метода замещения, устранения влияния вариации, исключение погрешности от мертвого хода, измерения одной величины несколькими независимыми методами, несколькими СИ, уравновешивание результатов измерений, связанных известным условием.

3.7. Точность полученных при измерении отсчетов и последующих вычислений при их обработке должна соответствовать требуемой точности результата измерений, обусловленной измерительной задачей.

Число разрядов при отсчете и в промежуточных вычислениях должно быть на единицу или две больше чем в окончательном результате.