Простейшие логические операции

Пусть даны два произвольных высказывания X и Y.

Ниже приведены таблицы истинности логических операций, используемых в высказываниях.

Отрицаниемвысказывания X называется высказывание 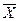, которое истинно, когда ложно X, и ложно когда X истинно.

Таблица истинности для отрицания.

X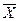

Конъюнкцией двух высказываний X и Y называется высказывание 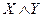, которое истинно только в том случае, когда X и Y оба истинны.

Таблица истинности для конъюнкций.

X	Y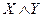

Дизъюнкциейдвух высказываний X и Y называется высказывание 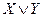, которое истинно, когда хотя бы одно из них истинно.

Таблица истинности для дизъюнкций.

X	Y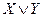

Импликациейдвух высказываний X и Y называется высказывание 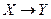, которое ложно тогда и только тогда, когда X истинно, а Y ложно.

Таблица истинности для импликаций.

X	Y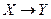

Эквивалентностьювысказываний X и Y называется высказывание 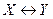, которое истинно тогда и только тогда, когда X и Y оба истинны или ложны.

Таблицы истинности для эквивалентности.

X	Y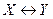

Для образования составных высказываний наряду с единичным использованием каждой основной связки можно пользоваться основными связками многократно, получая более сложные составные высказывания – аналогично тому, как с помощью основных арифметических операций образуются сложные алгебраические высказывания:

;

;

.

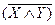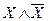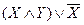Их следует читать «изнутри наружу» подобно алгебраическим выражениям, в которых сначала группируются величины, заключенные в самые внутренние скобки, затем эти скобки в свою очередь группируются и т.д. Если скобок нет, то операции надо выполнять в следующем порядке: отрицание (если оно стоит над простым высказыванием), конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание, если оно стоит над выражением. Каждое составное высказывание имеет свою таблицу истинности, которая может быть построена стандартным образом.

Два высказывания, имеющие одинаковые таблицы истинности, называются эквивалентными.

Проверку эквивалентности двух составных высказываний имеющих одни и те же компоненты, удобно осуществлять при помощи таблиц истинности.

Для этого достаточно лишь посмотреть, одинаковы ли таблицы истинности у этих составных высказываний.

Из следующей таблицы истинности видно, что 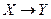эквивалентно .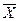

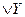X	Y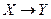

Тавтология и противоречие

Высказывание, истинное во всех случаях, называется логически истинным, или тавтологией. Каждое высказывание вида 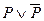- тавтология. Например: «Быть или не быть».

Высказывание, построенное так, что оно ложно в любом случае, называется логически ложным, или противоречием (опровержением).

Например, высказывание: «Она движется в направлении Самары и она не движется в направлении Самары» всегда ложно, т.к. нельзя делать одновременно и то, и другое, следовательно, это противоречие.

Пример тавтологии

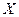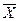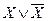Пример противоречия

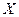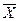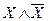Работу составила преподаватель Т.С. Пронина