Основные приемы построения и выполнения группировок
Если для построения группировки используется только один признак, то такую группировку называются простой, если группировка проводится по нескольким признакам, ее называют сложной. Сложная группировка бывает или комбинационная, или многомерная.
Комбинационная группировка выполняется последовательно: группы, выделенные по одному признаку, затем выделяются в подгруппы по другому признаку, которые, в свою очередь, могут выделяться по следующему другому признаку. В этом случае число групп будет равно произведению числа выделенных групп на число группировочных признаков. Процедура определения оптимального числа групп основана на применении формулы Стерджесса:
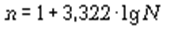
где n - число групп; N - число единиц совокупности.
Из формулы видно, что выбор числа групп зависит от объема совокупности. Если групп оказывается много и они включают малое число единиц, то групповые показатели могут стать ненадежными. Поэтому альтернативой комбинационной группировке является многомерная группировка, которая осуществляется по комплексу признаков одновременно. Ее применение требует использования электронной вычислительной техники. С помощью специально разработанных электронных программ формируются однородные группы на основании близости по всему комплексу признаков.
Определение числа групп тесно связано с понятием величина интервала: чем больше число групп, тем меньше величина интервала, и наоборот. Интервал - разница между максимальным и минимальным значениями признака в каждой группе. Он определяет количественные границы групп, что для статистической практики имеет большое значение, особенно когда нужно образовать качественно однородные группы. Например, исследуется совокупность предприятий по выполнению коллективных договоров. Здесь нельзя объединять предприятия, которые не выполнили обязательства, и те, которые их перевыполнили. Показатель здесь - величина интервала.
Другим примером является невозможность образовывать группу 95 - 105%, поскольку это разные части совокупности. Следует образовать две группы: 95 - 100% и 101 - 105%. В этом случае границы, по которым различаются совокупности, абсолютно соблюдаются.
Каждый интервал имеет нижнюю (наименьшее значение признака) и верхнюю (наибольшее значение признака) границы или одну из них. Поэтому величина интервала есть разность между верхней и нижней границами интервала. Если у интервала указана лишь одна граница (у первого - верхняя, у последнего - нижняя), то речь идет об открытых интервалах. Если у интервала имеются и нижняя, и верхняя границы, то речь идет о закрытых интервалах. Закрытые интервалы подразделяются на равные и неравные (прогрессивно возрастающие, прогрессивно убывающие), а также специализированные и произвольные.
Группировку с равными интервалами строят тогда, когда исследуются количественные различия в величине признака внутри групп одинакового качества, а также если распределение носит более или менее равномерный характер. Если можно заранее установить определенное количество групп, то величину равного интервала можно вычислить по формуле
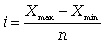
где i - величина равного интервала; xmax, xmin - наибольшее и наименьшее значения признака; n - число групп.
Если не требуется предварительного установления числа групп, то используется другой способ определения величины равного интервала - по формуле Стерджесса
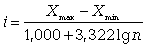
где n - число наблюдений.
Если величина равного интервала рассчитывается по данной формуле, то следует знаменатель предварительно округлить до целого числа (как правило, всегда большего), так как количество групп не может быть дробным числом.
В статистической практике чаще применяются неравные интервалы (постепенно возрастающие или постепенно убывающие). При этом исследуемая совокупность делится на группы примерно равного заполнения с большим числом единиц. Неравные интервалы могут использоваться, например, в таких случаях:
а) при исследовании группировки с применением нескольких признаков, дающих возможность составить несколько подгрупп, где требуются уже и более длинные и более короткие интервалы;
б) при образовании крупных групп с новым качеством на базе мелких групп при условии сохранения их однородности, что приводит к увеличению интервалов.
В статистической практике используются также специализированные интервалы. Интервалы называют специализированными, если речь идет об установлении границ интервала в группах, схожих по типу и по признаку, но имеющих отношение, скажем, к разным отраслям производства.
