Информационная характеристика процесса измерения

Всякое измерение можно рассматривать как цепь преобразований измеряемой величины до тех пор, пока результат измерений не будет представлен в том виде, который требовалось получить.

Процесс измерения характеризуется передачей информации о значении измеряемой величины от одного носителя ее к другому, т.е. преобразованием информации о значении измеряемой величины в результат измерений. Это означает, что в информационном аспекте измерение можно рассматривать как процесс приема и преобразования информации от измеряемой величины в целях получения количественного результата путем сравнения с принятой шкалой или единицей измерения в форме, наиболее удобной для дальнейшего использования ее человеком и машиной. Для установления связи между точностью измерений и количеством получаемой при измерениях информации используют основные положения теории информации. При этом под термином "информация" понимают совокупность сведений о каком-либо объекте, процессе или явлении, в общем случае – о физической системе. Задачей получения информации является устранение неопределенности в наших представлениях о состоянии некоторой физической системы и установление количественных закономерностей, связанных с получением, обработкой и хранением информации. Рассмотрим характеристику процесса измерения с позиций теории информации. В теории информации получению абсолютной и относительной приведенной погрешностей придается вероятностный, статистический смысл, а итог проведенного измерения рассматривается как сокращение области неопределенности измеряемой величины. Предел измерения от Х₁ до Х₂ (рис. 2.3) с позиций теории информации означает, что вероятность получения отсчетов где-то в пределах Х₁ и Х₂ равна единице. Если считать, что плотность вероятности распределения различных значений измеряемой величины вдоль всей шкалы прибора одинакова, то наша осведомленность о значении величины до измерения может быть представлена графиком распределения плотности вероятности P(x) вдоль шкалы (см. рис. 2.3). Плотность распределения вероятности в этом случае равна:

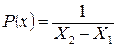. (2.12)

Как показано на рис. 2.3, в результате измерения получено показание прибора Х_n. Однако, учитывая погрешности измерения, мы принимаем результат X_n ± D. Это значит, что действительное значение измеряемой величины лежит где-то в пределах от Х_n- до Х_n+, т.е. в пределах участка 2D. Согласно теории информации, результат измерения можно характеризовать так: если до измерения область неопределенности находилась от Х₁ до Х₂ и имела малую плотность вероятности, то после измерения неопределенность сократилась до 2D и имеет значительную плотность Р(х)=1/2D. Следовательно, получение какой-либо информации об интересующей нас величине заключается в уменьшении неопределенности ее значения. Математически это положение выражается формулой

M = H(Х) - H(x/x_n), (2.13)

где M – количество полученной информации,

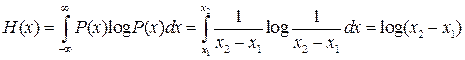(2.14)

исходная энтропия,

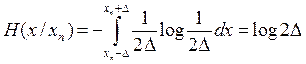. (2.15)

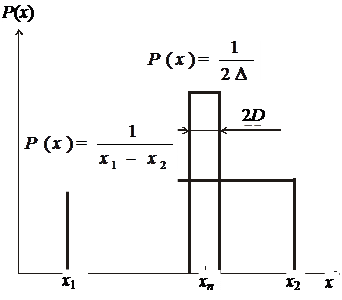Рис. 2.3. График распределения плотности вероятности P(x) вдоль шкалы x

Полученное количество информации, равное разности исходной и оставшейся энтропии, равно

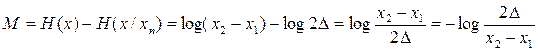, (2.16)

т.е. количество информации M определяется уменьшением энтропии от значения H(x), характеризующей неопределенность искомой величины перед измерением, до значения H(x/x_n), которое остается после показания прибора.

Таким образом, получение любой информации, в том числе и измерительной, теория информации рассматривает как устранение некоторой неопределенности, а количество информации рассматривается как разность ситуации до и после получения данного сообщения. В настоящее время, по мнению специалистов, развивающих и использующих информационную теорию измерительных устройств, использование методов теории информации обеспечит более эффективную оценку качества приборов.