Использование сетей Петри при переходе от грамматики к минимальному автомату.

Возвратившись к заданной праволинейной грамматике, построим для нее сеть Петри. Это можно сделать, поставив в соответствие нетерминальным символам позиции сети, а терминалам - переходы.

Рисунок 4

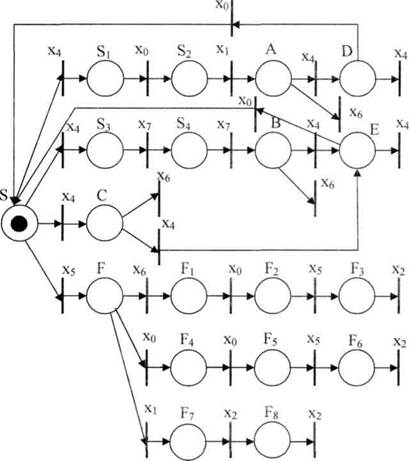
Получившаяся на рис.4 сеть является автоматной сетью Петри, ее позиции можно трактовать как состояния конечного автомата, а переходы - как входные символы. Способом, аналогичным рассмотренному в п. 4 устраним недетерминированность автомата, а для полноты соответствия построенной сети Петри распознающему автомату Мура введем заключительную позицию Z, в которую направим дуги из всех переходов, ранее не имеющих исходящих дуг. Окончательно придем к рис. 5.

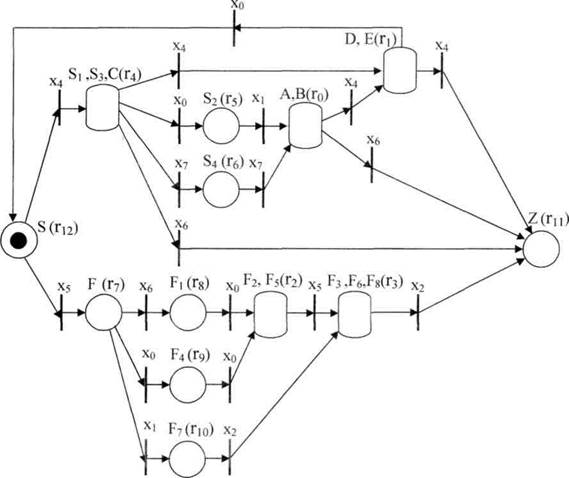Рисунок 5

Размещение состояний автомата.

Один из способов размещения состояний синхронного автомата состоит в произвольном назначении им кодовых наборов. Рассмотрим такое размещение для нашего случая. Состоянию r_i поставим в соответствие вершину 4-мерного куба с десятичным номером i, который определяется по значения ее двоичных координат z₁, z₂, z₃, z₄ в соответствии с формулой

i= z₁2⁰+z₂2¹+z₃2²+z₄2³. Число внутренних переменных, изменяющих свои значения при переходе автомата из одного состояния в другое, есть расстояние по Хеммингу между этими состояниями. Очевидно, что чем меньше внутренних переменных изменяется при каждом переходе автомата, тем меньше конституент единицы содержат их переключательные функции. В силу этого второй вариант размещения состояний может выполняться в соответствии с критериями минимальности по Хеммингу по всем переходам. Суть такого размещения заключается в максимально возможном использовании соседних кодов. Коды состояний называются соседними, если при переходе автомата из одного состояния в другое изменяет свое значение лишь одна кодирующая переменная.

Собственно кодирование состоит во вложении графа переходов автомата в куб, соответствующий минимальной размерности (в данном случае - в 4 - мерный куб). Вложение будем осуществлять неформально, методом проб и ошибок. В результате придем к картинке на рис.6.

Рисунок 6

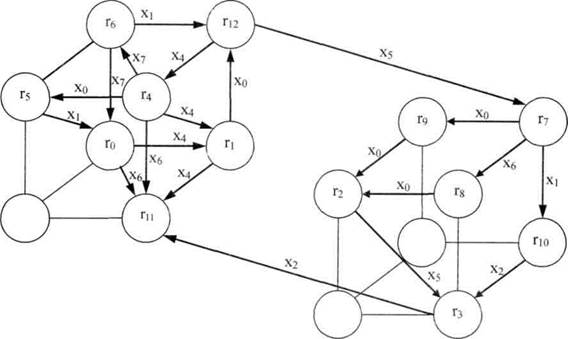
Оказалось, что из 22 возможных переходов 17 являются соседними, а 5 имеют расстояние 2. Значение принятого критерия размещения (суммарного расстояния по Хеммингу по всем возможным переходам) в данном случае равно 27. Возможно, существует более эффективное размещение, однако установление этого факта связано с перебором очень большого числа вариантов.