Отношением строгого порядка
Отношение  в множестве
в множестве  такое, что выполняются свойства антирефлексивности, асимметричности, транзитивности.
такое, что выполняются свойства антирефлексивности, асимметричности, транзитивности.
Отношение толерантности
Отношение  в множестве
в множестве  такое, что выполняются свойства рефлексивности и симметричности.
такое, что выполняются свойства рефлексивности и симметричности.
Отображение
Бинарное отношение 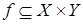 из множества
из множества  в множество
в множество  такое, что область определения функции
такое, что область определения функции 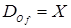 , область значений функции
, область значений функции 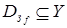 и из
и из 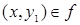 ,
, 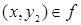 следует, что
следует, что 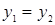 .
.
Отношения-операнды
Отношения, к которым применяется операция реляционной алгебры.
Отношение частичного порядка
То же, что и отношение нестрогого порядка.
Отношение эквивалентности
Отношение в множестве  для которого выполняются свойства рефлексивности, симметричности, транзитивности.
для которого выполняются свойства рефлексивности, симметричности, транзитивности.
Пересечение отношений
Теоретико-множественная операция над отношениями. При выполнении операции пересечения двух отношений получаем отношение, включающее только те кортежи, которые входят в оба отношения-операнда.
Полное
Отношение 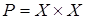 , которое имеет место для каждой пары
, которое имеет место для каждой пары 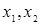 элементов из
элементов из 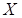 .
.
Полностью упорядоченное множество
То же, что и линейно упорядоченное множество (или цепь).
Полный порядок
То же, что и линейный порядок.
Проекция отношений
Операция реляционной алгебры. При выполнении проекции отношения на заданный набор его атрибутов отношение-результат получается путем удаления из отношения-операнда атрибутов, не указанных в заданном наборе.
Прообраз
Если множество 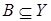 , то множество
, то множество 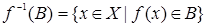 называется прообразом множества
называется прообразом множества  относительно отображения
относительно отображения  .
.
Пустое отношение
Отношение в  , которому не удовлетворяет ни одна пара элементов из
, которому не удовлетворяет ни одна пара элементов из  .
.
Разность отношений
Теоретико-множественная операция над отношениями. Отношение, являющееся разностью двух отношений, включает все кортежи, входящие в отношение-первый операнд, такие, что ни один из них не входит в отношение, являющееся вторым операндом.
Рефлексивность
Отношение 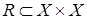 называется рефлексивным, если
называется рефлексивным, если 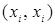 принадлежит
принадлежит  для всех
для всех 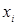 из
из  , т.е. оно всегда выполняется между объектом и им самим (
, т.е. оно всегда выполняется между объектом и им самим ( 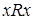 ).
).
Реляционная алгебра
Алгебра 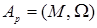 , в которой
, в которой 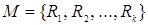 - множество отношений, составляющих базу данных, а сигнатура
- множество отношений, составляющих базу данных, а сигнатура 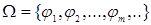 кроме операций объединения, пересечения, разности, декартова произведения включает специальные операции над отношениями: ограничение отношений (выбор), проекцию отношений, соединение отношений, деление отношений.
кроме операций объединения, пересечения, разности, декартова произведения включает специальные операции над отношениями: ограничение отношений (выбор), проекцию отношений, соединение отношений, деление отношений.
Реляционная модель данных
Модель данных, которая с математической точки зрения является табличным представлением данных (двумерная таблица).
Сечение отношения
Если 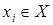 , то сечение отношения
, то сечение отношения  по элементу
по элементу 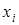 , обозначаемое
, обозначаемое 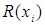 , есть множество
, есть множество 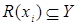 , состоящее из элементов
, состоящее из элементов 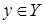 таких, что
таких, что 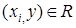 , т.е.
, т.е. 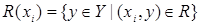 .
.
Симметричное отношение
То же, что и обратное отношение.
Симметричность
Отношение 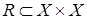 называется симметричным, если
называется симметричным, если 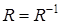 , т.е. при выполнении соотношения
, т.е. при выполнении соотношения 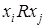 выполняется и соотношение
выполняется и соотношение 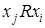 (
(  выполняется либо в обе стороны, либо не выполняется вообще).
выполняется либо в обе стороны, либо не выполняется вообще).
