Алгоритм решения задачи о максимальном потоке.

Специальные свойства.

1) Рефлексивность. Отношение рефлексивно, если на главной диагонали стоят единицы и антирефлексивно, если на главной диагонали нули. Поскольку на главной диагонали есть как нули, так и единицы, R не является ни рефлексивным, ни антирефлексивным (то есть общего вида).

2) Симметричность. Находим транспонированную матрицу (то есть матрицу обратного отношения:

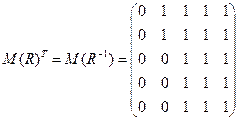
Отношение является симметричным, если 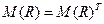(т.е. матрица симметрическая) и антисимметричным, если у матрицы 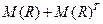нет двоек вне главной диагонали (i,j-й элемент равен двойке, если ).

.

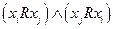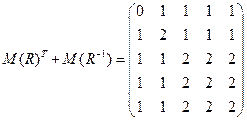В данном примере R не является ни симметричным, ни антисимметричным.

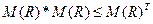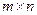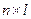3) Транзитивность. Отношение является транзитивным, если (имеется в виду поэлементное неравенство – каждый элемент левой матрицы меньше или равен соответствующего элемента правой матрицы) . Операция С=A *B – это булево умножение булевых матриц размерности и (соответствует композиции отношений), определяемое по формуле «строка на столбец»: 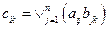. Матрица С имеет размерность 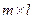и также может быть получена из обычного произведения AB заменой всех ненулевых элементов на единичные. В данном примере

.

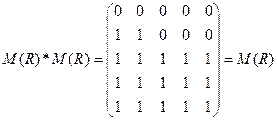Следовательно, 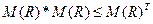и отношение R транзитивно.

Построим орграф отношения G(R). Вершины этого орграфа – это элементы множества A, дуги – элементы R (вершины x и y соединяются дугой, если xRy).

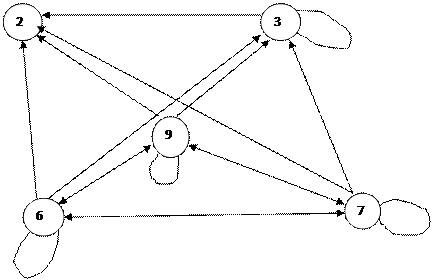Замечание

Специальные свойства отношения можно проверять также исходя из их определений (требуется обоснованный ответ). Рефлексивность, антирефлексивность, симметричность, антисимметричность, нетранзитивность также можно определять по графу.

Даны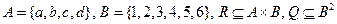

,

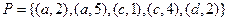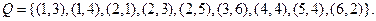
Найдите отношение 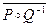, его область определения и область значений.

Решение

Матричный способ

Матрица отношения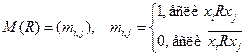

При этом ;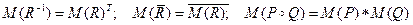

Здесь 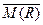– поэлементное отрицание, 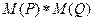– булево произведение. [Операция С=A *B – это булево умножение булевых матриц размерност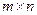и и 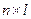(соответствует композиции отношений), определяемое по формуле «строка на столбец»: 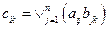. Матрица С имеет размерность 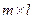и также может быть получена из обычного произведения AB заменой всех ненулевых элементов на единичные. ]

; ;

;

; ;

;

/; .

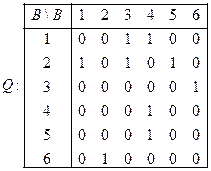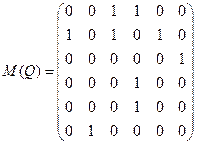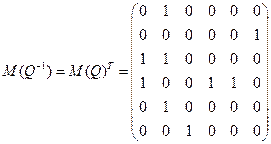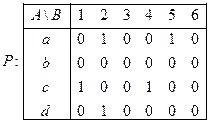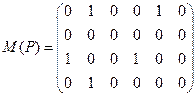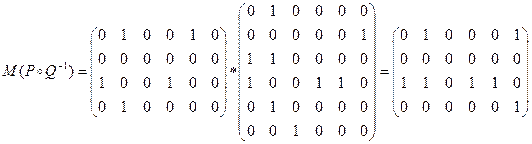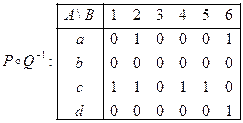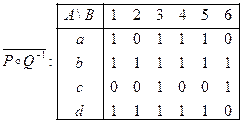Ответ: 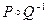={(a,2),(a,6),(c,1),(c,2),(c,4),(c,5),(d,6)}. ; ;

=

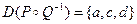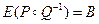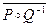={(a,1),(a,3),(a,4),(a,5),(b,1),(b,2),(b,3),(b,4),(b,5),(b,6),(c,3),(c,6),(d,1),(d,2),(d,3),(d,4),(d,5)}

a	b	a&b	aÚb	a®b	a~b	aÅb

x1

x2

f0

f1 x1Ùx2

f2

f3 x1

f4

f5 x2

f6 x1Åx2

f7 x1Úx2

f8 x1¯x2

f9 x1~x2

f10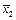

f11 x2®x1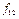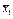

f13 x1®x2

f14 x1½x2

f15

Имеют место следующие равносильности:

1) 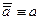– закон двойного отрицания;

2) , 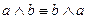– коммутативность дизъюнкции и конъюнкции;

3) 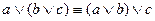, 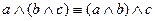– ассоциативность дизъюнкции и конъ­юнк­ции;

4) 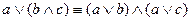, 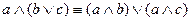– взаимная дистрибутивность дизъюнкции и конъюнкции;

5) 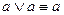, 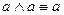– законы идемпотентности;

6) 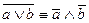, – законы де Моргана;

7) 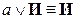, , 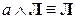, 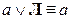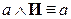– законы истины и лжи;

8) , 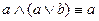– законы поглощения;

9) 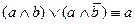– закон склеивания;

10) 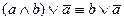– закон вычёркивания;

11) 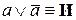– закон исключённого третьего;

12) 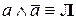– закон противоречия.

Доказательство: прямая проверка с помощью таблиц истинности.

Определение. Булева функция f^*(x₁, …, x_n) называется двойственной булевой функции f(x₁, …, x_n), если она получена из f(x₁, …, x_n) инверсией всех аргументов и самой функции, то есть

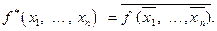
Пример. Построим функцию, двойственную стрелке Пирса.

Представление булевой функции 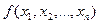в виде дизъ­юнк­ции не­сов­па­да­ю­щих элементарных кон­ъюнкций называется дизъюнктивной нор­маль­ной фор­мой (ДНФ) этой функции. Если каж­дая вхо­дя­щая в ДНФ эле­мен­тар­ная конъюнкция яв­ля­ется пол­ной (относительно набора переменных 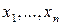), то ДНФ называется со­вер­шен­ной дизъ­юнк­тивной нормальной формой (СДНФ).

Совершенная конъюнктивная нормальная форма

Напишем СДНФ для функции :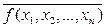

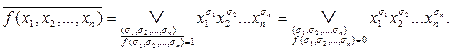
Применим к обеим частям этого равенства операцию отрицания, учитывая закон двой­но­го отрицания получим:

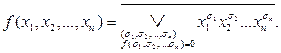
Применим законы де Моргана:

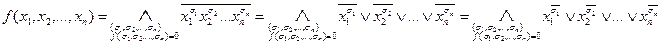
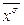
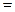
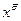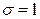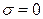(мы воспользовались тем, что ; это легко проверяется просмотром слу­чаев и ). Таким образом, справедлива следующая теорема:

Теорема 2.9.Любую функцию можно представить в виде

.

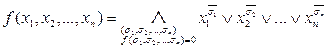Определение 2.4. Формула вида 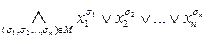, где M — некоторое мно­же­с­т­во битовых строк длины n, называется совершенной конъюнктивной нор­маль­ной фор­мой (СКНФ)(для набора булевых переменных ).

Построение многочлена Жегалкина по СДНФ.

Построение многочлена Жегалкина методом неопределённых коэффициентов.

Метод треугольника.

x y z f треугольник Паскаля слагаемые
0 0 0 0 0 0 1 1 0 1 0 1 1
0 0 1 0 0 1 0 1 1 1 1 z
0 1 0 1 1 1 1 0 0 0 y
0 1 1 1 0 0 1 0 0 yz
1 0 0 0 0 1 1 0 x
1 0 1 1 1 0 1 xz
1 1 0 0 1 1 xy
1 1 1 1 0 xyz

Полином Жегалкина: f(x, y, z) = y⊕xz⊕xy

В зарубежной литературе представление в виде полинома Жегалкина (основное применение – в криптографии) обычно называется алгебраической нормальной формой (АНФ).

Минимизация ДНФ по карте Карно

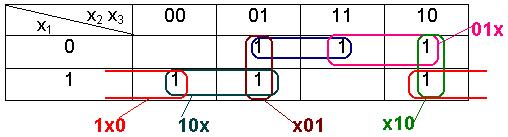
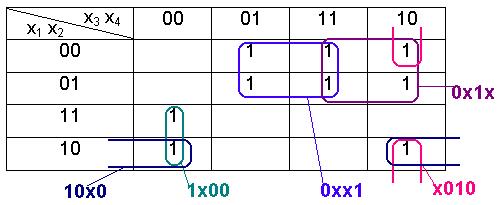
Пример. Минимизировать ДНФ булевой функции 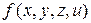, заданной строкой зна­че­ний (1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0).

Применяя алгоритм Куайна, представим данную функцию сокращённой ДНФ:

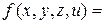(представляем в виде СДНФ) = (проводим обобщённое склеивание)

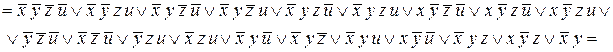
(проводим поглощение)

.

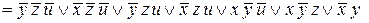Строим таблицу Квайна:

	´						´
	´		´
		´							´
		´				´
							´	´
								´	´
			´	´	´	´

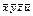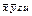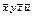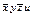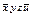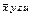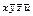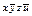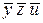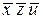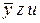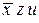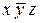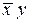Если в столбце лишь один крестик, то соответствующую строку надо выбрать обя­за­тель­но; это строка 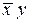. Далее вычеркиваем все столбцы, на пересечении которых с уже вы­бранной строкой стоят крестики (это столбцы 3, 4, 5, 6). В каждом из оставшихся столб­цов стоят два крестика. Множество оставшихся строк имеет 4 минимальных под­мно­жества, удовлетворяющих требованию, чтобы каждый из невычеркнутых столбцов имел крестик хотя бы в одной из строк данного подмножества; выпишем эти под­мно­же­с­тва, обозначая строки их номерами:

.

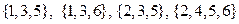Таким образом, для рассматриваемой функции имеется 4 тупиковых ДНФ:

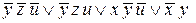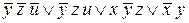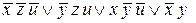, , и .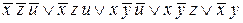

Первые три из них являются МДНФ.

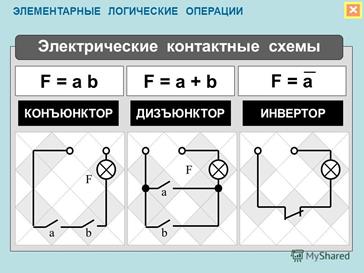
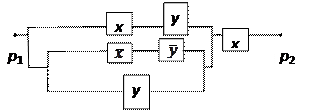
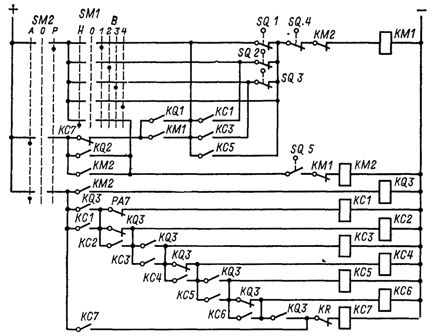
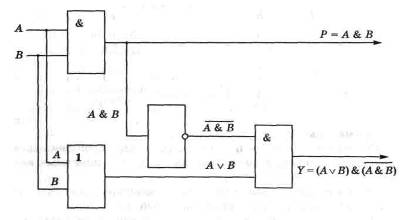
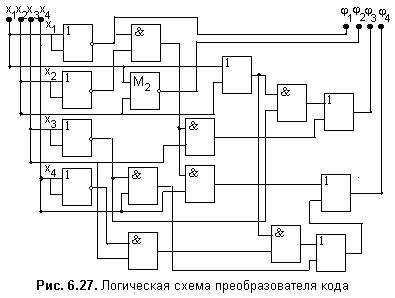
Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).

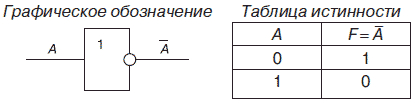
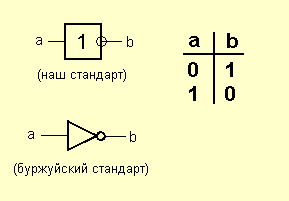
1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).

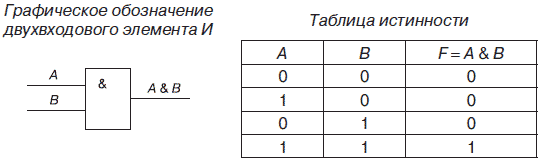
2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.

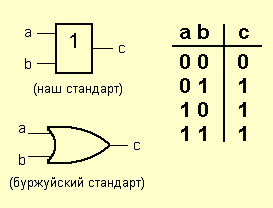
3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.

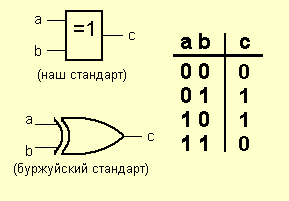
Европейский стандарт (Европа и бывший СССР) и стандарт ANSI:

"Исключающее ИЛИ" (XOR)

Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети).

Алгоритм решения задачи о максимальном потоке.

1°. Положить f=Df=0, c = пропускным способностям заданной транспортной сети.

2°. Переприсвоить: f=f+Df. Вычислить остаточные пропускные способности Dc, от­ве­ча­ющие пропускным спо­соб­ностям c и потоку Df.

3°. Для транспортной сети спропускными способностями Dc найти путь l из s в t, об­ла­да­ющий максимальной про­пуск­ной способностью. Пусть j — пропускная спо­соб­ность это­го пути. Если j=0 (путь отсутствует), то перейти к пункту 4°; в про­тив­ном случае переопределить добавочный поток Df, полагая

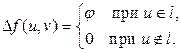
После этого перейти к пункту 2°.

4°. Закончить работу алгоритма. Поток f — ответ задачи.

Пусть функ­ция c описывает пропускные способности исходной сети и f — стан­дарт­ный пред­ста­ви­тель исходного потока. Тогда остаточные пропускные способности Dc оп­ре­деляются следующим образом:

Dc(u, v)=c(u, v)-f(u, v)+ f(v, u).

Пример решения задачи

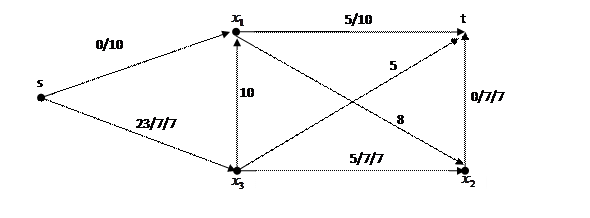
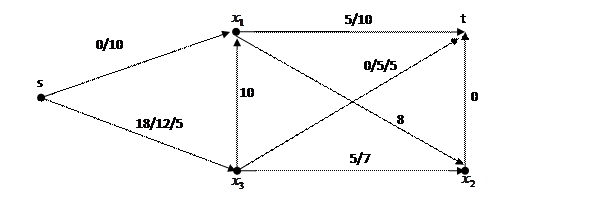
Задан граф транспортной сети

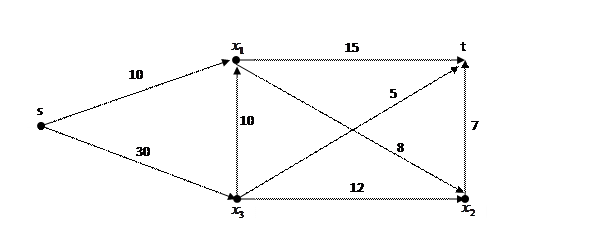
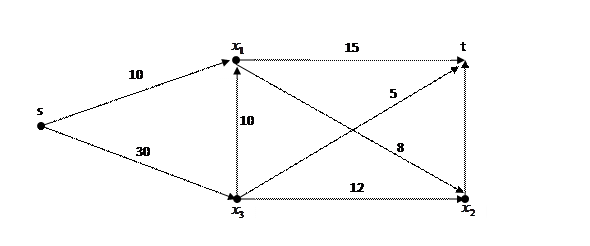
Составляем матрицу пропускных способностей:

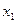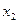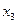				t
s

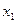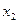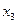Находим путь из s в t как можно большей пропускной способности. Путь максимальной пропускной способности можно найти с помощью алгоритма волны, а для небольшой сети – визуально по графу.

Примечание1

Если найден путь не максимальной пропускной способности, алгоритм всё равно даст результат, но число шагов может увеличиться.

Примечание2

При решении задачи можно использовать как язык матриц, так и язык графов. Ниже приводятся оба способа записи решения.

Путь 1. 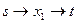. Пропускная способность: 10. Составляем матрицу остаточных пропускных способностей/добавочного потока

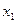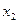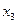				t
s	0/10
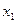				5/10

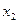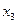При отображении данной информации на графе будем использовать формат

A/B/C, где A = c(u,v) – остаточная пропускная способность дуги, B = c(v,u) – остаточная пропускная способность противоположной дуги, C= f(u,v) – добавочный поток через данную дугу. Для дуг, через которые добавочный поток не идёт, третья компонента отсутствует. Остаточные пропускные способности дуг, входящих из s и дуг, исходящих из t вычислять не нужно, на графе они присутствуют для большей наглядности.

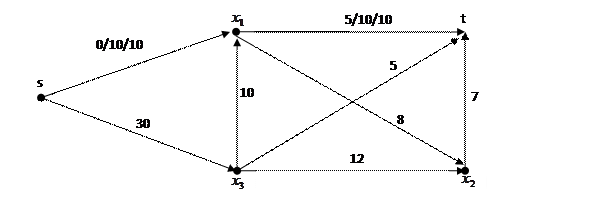
Путь 2. . Пропускная способность: 7. Матрица остаточных пропускных способностей/добавочного потока:

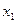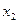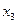				t
s			23/7
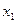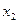				0/7
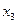		5/7

Соответствующий граф:

Путь 3. 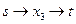. Пропускная способность: 5. Матрица остаточных пропускных способностей/добавочного потока:

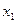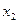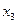				t
s			18/5
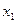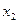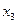				0/5

Соответствующий граф:

Путь 4. 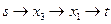. Пропускная способность: 5. Матрица остаточных пропускных способностей/добавочного потока:

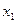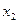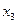				t
s			18/5
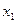				0/5
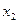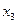	5/5

Соответствующий граф:

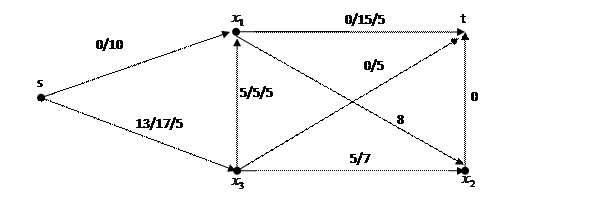
Путь 5. Отсутствует. Алгоритм завершён.

Максимальный поток: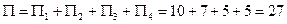

Находим проверочный разрез (минимальное сечение). Все дуги, входящие в проверочный разрез, должны быть насыщенными (иметь остаточную пропускную способность 0). В нашем случае это дуги 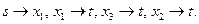Искомый разрез (он может быть не единственным) составляют дуги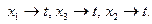

Графическое изображение проверочного разреза:

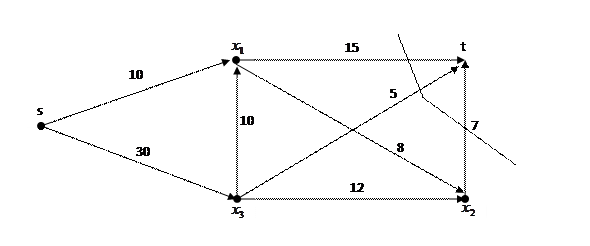
Пропускная способность данного разреза равна 15+5+7=27=П, что соответствует теореме Форда-Фалкерсона.