Тема 6. Разновидности дедуктивных умозаключений

1. Что такое простой силлогизм? Что такое фигуры и модусы простого силлогизма?

2. Каковы правила простого силлогизма?

3. Что такое разделительно-категорическое умозаключение?

4. Что такое условно-категорическое умозаключение?

1. Что такое простой силлогизм? Что такое фигуры и модусы простого силлогизма?

Если в дедуктивном умозаключении и посылки, и вывод являются простыми суждениями (A, I, E, O; см. тему 4), то такое умозаключение называется простым, или категорическим силлогизмом.

Рассмотрим пример простого силлогизма.

Все цветы (М) – это растения (Р).

Все розы (S)– это цветы (М).

Все розы (S)– это растения (Р).

Обе посылки и вывод являются в данном силлогизме простыми суждениями (причем и посылки, и вывод – это суждения вида А (общеутвердительные)). Обратим внимание на вывод, представленный суждением: Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Также в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы возможно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.

1. Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).

2. Предикат вывода располагается в первой посылке силлогизма и называется большим термином силлогизма(первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия розы и растения находятся в отношении родо-видового подчинения), в силу чего предикат вывода назван большим термином, а субъект вывода – меньшим.

3. Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизмаи обозначается латинской буквой М, потому что «средний» на латинском – это medium.

Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т.е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.

Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:

Все газы (М) – это химические элементы (Р).

Гелий (S)– это газ (М).

Гелий (S)– это химический элемент (Р).

Учитывая то, что в первой посылке средний термин связан с предикатом, во второй субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере:

М Р

S M

________________________

S P

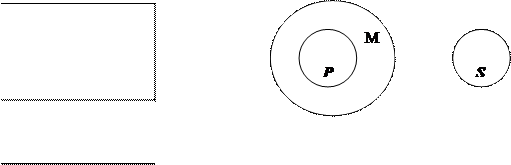
Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, можно изобразить отношения между тремя терминами с помощью кругов Эйлера. В данном случае получится следующая схема:

Р

М

S

Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например:

Все рыбы (Р)дышат жабрами (М).

Все киты (S)не дышат жабрами (М).

Все киты (S)не рыбы (Р).

Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так:

Р М

S M

_____________________

S P

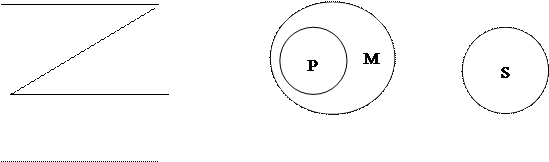
Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:

Все тигры (М)– это млекопитающие (Р).

Все тигры (М)– это хищники (S).

Некоторые хищники (S)– это млекопитающие (Р).

Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма:

М Р

S M P

М S

______________________

S P

Четвертая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:

Все квадраты (Р)– это прямоугольники (М).

Все прямоугольники (М)– это не треугольники (S).

Все треугольники (S)– это не квадраты (Р).

Схемы взаимного расположения терминов и отношений между ними в четвертой фигуре силлогизма:

Р М

М S

______________________

S P

(Отметим, что отношения между терминами силлогизма во всех фигурах могут быть и другими).

Любой простой силлогизм состоит из трех суждений (двух посылок и вывода). Каждое из них является простым и принадлежит к одному из четырех видов (А, I, Е, О). Набор простых суждений, входящих в силлогизм, называется модусом простого силлогизма. Например, в силлогизме:

Все небесные тела движутся.

Все планеты – это небесные тела.

Все планеты движутся.

первая посылка является простым суждением вида А (общеутвердительным), вторая посылка – это тоже простое суждение вида А, и вывод в данном случае представляет собой простое суждение вида А. Поэтому рассмотренный силлогизм имеет модус ААА. Силлогизм:

Все журналы – это периодические издания.

Все книги не являются периодическими изданиями.

Все книги не являются журналами.

имеет модус АЕЕ. Силлогизм:

Все углероды – простые тела.

Все углероды электропроводны.

Некоторые электропроводники – простые тела.

имеет модус ААI. Всего модусов во всех четырех фигурах, т.е. возможных комбинаций простых суждений в силлогизме, – 256. В каждой фигуре 64 модуса. Однако из всех этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность ее выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные – неправильными.

2. Каковы правила простого силлогизма?

Истинность посылок простого силлогизма сама по себе не гарантирует истинности его выводов, для последней требуется соблюдение нескольких правил силоллогизма. Рассмотрим основные из них.

1. В силлогизме должно быть только три термина. Обратимся к уже упоминавшемуся (см. тему 1) примеру силлогизма, в котором данное правило нарушено:

Движение вечно.

Хождение в школу – это движение.

Хождение в школу вечно.

Обе посылки этого силлогизма являются истинными суждениями, однако из них вытекает ложный вывод, потому что нарушено рассматриваемое правило. Термин движение употребляется в двух посылках в двух разных смыслах (движение как всеобщее мировое изменение и движение как механическое перемещение тела из точки в точку), и получается, что терминов в силлогизме три (движение, хождение в школу, вечность), а смыслов (поскольку один из терминов употребляется в двух разных смыслах) четыре, т.е. лишний смысл как бы подразумевает лишний термин. Иначе говоря, в приведенном примере силлогизма было не три, а четыре (по смыслу) термина. Ошибка, возникающая при нарушении вышеприведенного правила, называется учетверением терминов.

2. Средний термин должен быть распределен хотя бы в одной из посылок. О распределенности терминов в простых суждениях говорилось в теме 4. Напомним, что проще всего устанавливать распределенность терминов в простых суждениях с помощью круговых схем: надо изобразить кругами Эйлера отношения между терминами суждения, при этом полный круг на схеме будет обозначать распределенный термин (+), а неполный – нераспределенный (–). Рассмотрим пример силлогизма:

Все кошки – это живые существа.

Сократ – это тоже живое существо.

Сократ – это кошка.

Из двух истинных посылок вытекает ложный вывод. Изобразим кругами Эйлера отношения между терминами в посылках силлогизма и установим распределенность этих терминов:

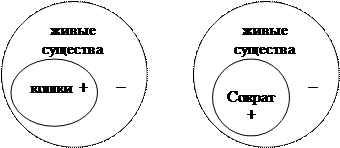1 посылка 2 посылка

Как видим, средний термин (живые существа) в данном случае нераспределен ни в одной из посылок, а по правилу он должен быть распределен хотя бы в одной из посылок. Ошибка, возникающая при нарушении рассматриваемого правила, так и называемая – нераспределенность среднего термина в каждой посылке.

3. Термин, который был нераспределен в посылке, не может быть распределен в выводе.Обратимся к следующему примеру:

Все яблоки съедобны.

Все груши – это не яблоки.

Все груши несъедобны.

Посылки силлогизма являются истинными суждениями, а вывод – ложным. Как и в предыдущем случае, изобразим кругами Эйлера отношения между терминами в посылках и в выводе силлогизма и установим распределенность этих терминов:

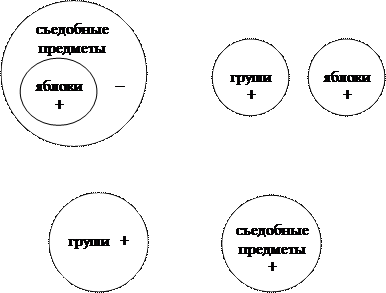1 посылка 2 посылка

вывод

В данном случае предикат вывода, или больший термин силлогизма (съедобные предметы) в первой посылке является нераспределенным (–), а в выводе – распределенным (+), что запрещается рассматриваемым правилом. Ошибка, возникающая при его нарушении, называется расширением большего термина. (Вспомним, что термин распределен, когда речь идет обо всех предметах, входящих в него и нераспределен, когда речь идет о части предметов, входящих в него, именно поэтому ошибка и называется расширением термина).

4. В силлогизме не должно быть двух отрицательных посылок.Хотя бы одна из посылок силлогизма должна быть утвердительной (могут быть утвердительными и обе посылки). Рассмотрим пример:

Снайперы не могут иметь плохое зрение.

Все мои друзья – не снайперы.

Все мои друзья имеют плохое зрение.

Обе посылки в силлогизме являются отрицательными суждениями и, несмотря на их истинность, из них вытекает ложный вывод. Ошибка, которая возникает в данном случае, так и называется – две отрицательные посылки.

3. Что такое разделительно-категорическое умозаключение?

В разделительно-категорическом умозаключении, как явствует из названия, первая посылка представляет собой разделительное, или дизъюнктивное суждение, а вторая посылка – это простое, или категорическое суждение. Например:

Учебное заведение может быть начальным или средним, или высшим.

МГУ является высшим учебным заведением.

МГУ – это не начальное и не среднее учебное заведение.

Разделительно-категорическое умозаключение имеет два модуса. В утверждающе-отрицающем модусе, который также называют модусом понендо толленс (лат. modus ponendo tollens)первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, во второй посылке утверждается один из них, а в выводе отрицаются все остальные (таким образом, рассуждение движется от утверждения к отрицанию). Например:

Леса бывают хвойными или лиственными, или смешанными.

Этот лес хвойный.

Этот лес не лиственный и не смешанный.

С помощью условных обозначений логических союзов можно представить форму данного умозаключения в виде следующей записи: ((аÚвÚс)Ùа)®(ØвÙØс), где (аÚвÚс) – это первая посылка в виде строгой дизъюнкции трех простых суждений; а – это вторая посылка в виде утверждения одного из них; ((аÚвÚс)Ùа) – это две посылки умозаключения, соединенные знаком конъюнкции; (ØвÙØс) – это вывод умозаключения в виде конъюнкции отрицаний двух оставшихся простых суждений, входивших в первую посылку; знак импликации (®) показывает, что из посылок следует вывод.

В отрицающе-утверждающем модусе, который также называют модусом толлендо поненс (лат. modus tollendo ponens)первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, во второй посылке отрицаются все данные варианты, кроме одного, а в выводе утверждается этот один оставшийся вариант (таким образом, рассуждение движется от отрицания к утверждению). Например:

Люди бывают европеоидами, или монголоидами, или негроидами.

Этот человек не монголоид и не негроид.

Этот человек является европеоидом.

С помощью условных обозначений логических союзов можно представить форму данного умозаключения в виде следующей записи: ((аÚвÚс)Ù(ØвÙØс))®а.

В разделительно-категорическом умозаключении следует соблюдать несколько правил.

1. Деление в первой посылке должно проводиться по одному основанию.Например, умозаключение:

Транспорт бывает наземным или подземным, или водным, или воздушным, или общественным.

Пригородные электропоезда – это общественный транспорт.

Пригородные электропоезда – это не наземный, не подземный, не водный и не воздушный транспорт.

построено по утверждающе-отрицающему модусу, но из двух истинных посылок вытекает ложный вывод. Почему так получается? Потому что в первой посылке деление проводилось по двум разным основаниям (в какой природной среде передвигается транспорт и кому он принадлежит; см. тему 3). Подмена основанияделения в первой посылке разделительно-категорического умозаключения приводит к ложному выводу.

2. Деление в первой посылке должно быть полным.Например, в умозаключении:

Математические действия бывают сложением или вычитанием, или умножением, или делением.

Логарифмирование – это не сложение, не вычитание, не умножение и не деление.

Логарифмирование – это не математическое действие.

неполное делениев первой посылке обусловливает ложный вывод, вытекающий из истинных посылок.

3. Результаты деления в первой посылке не должны пересекаться, или дизъюнкция должна быть строгой. Например, в умозаключении:

Страны мира бывают северными или южными, или западными, или восточными.

Канада – это северная страна.

Канада – это не южная, не западная и не восточная страна.

вывод является ложным, т.к. Канада в такой же степени северная страна, в какой и западная. Ложный вывод при истинных посылках объясняется в данном случае пересечением результатов деленияв первой посылке, или, что одно и то же, – нестрогой дизъюнкцией.Следует отметить, что нестрогая дизъюнкция в разделительно-категорическом умозаключении допустима в том случае, когда он построен по отрицающе-утверждающему модусу. Например, в умозаключении:

Он силен от природы или же – постоянно занимается спортом.

Он не является сильным от природы.

Он постоянно занимается спортом.

нет ошибки, несмотря на то, что дизъюнкция в первой посылке была нестрогой. Таким образом, рассматриваемое правило безоговорочно действует только для утверждающе-отрицающего модуса разделительно-категорического умозаключения.

4. Деление в первой посылке должно быть последовательным. Например, в умозаключении:

Предложения бывают простыми или сложными, или сложносочиненными.

Это предложение сложносочиненное.

Это предложение не простое и не сложное.

ложный вывод следует из истинных посылок по той причине, что в первой посылке был допущен скачок в делении.

4. Что такое условно-категорическое умозаключение?

В условно-категорическом умозаключенипервая посылка является условным, или импликативным суждением. Вторая его посылка представляет собой простое, или категорическое суждение. Например:

Если взлетная полоса покрыта льдом, то самолеты не могут взлетать.

Сегодня взлетная полоса покрыта льдом.

Сегодня самолеты не могут взлетать.

Условно-категорическое умозаключение имеет два модуса. В утверждающем модусе, который также называют модусом поненс (лат. modus ponens) первая посылка представляет собой импликацию, состоящую, как мы уже знаем, из двух частей – основания и следствия, вторая посылка является утверждением основания, а в выводе утверждается следствие. например:

Если вещество – металл, то оно электропроводно.

Данное вещество – это металл.

Данное вещество электропроводно.

Форма утверждающего модуса условно-категорического умозаключения: ((а®в)Ùа)®в, где (а®в) – это первая посылка в виде импликации основания (а) и следствия (в); ((а®в)Ùа) – это две посылки умозаключения в виде двухчленной конъюнкции, состоящей из уже упомянутой импликации и утверждения основания; в – это вытекающий из посылок вывод умозаключенияв виде утверждения следствия.

В отрицающем модусе, который также называют модусом толленс (лат. modus tollens)первая посылка представляет собой импликацию основания и следствия, вторая посылка является отрицанием следствия, а в выводе отрицается основание. Например:

Если вещество – металл, то оно электропроводно.

Данное вещество неэлектропроводно.

Данное вещество – не металл.

Форма отрицающего модуса условно-категорического умозаключения: ((а®в)ÙØв)®Øа.

Необходимо обратить внимание на уже известную нам особенность импликативного суждения, которая состоит в том, что основание и следствие нельзя поменять местами. Например, высказывание: Если вещество – металл, то оно электропроводно является верным, т.к. все металлы – это электропроводники (из того, что вещество – металл, с необходимостью вытекает его электропроводность). Однако, высказывание: Если вещество электропроводно, то оно – металл, неверно, т.к. не все электропроводники являются металлами (из того, что вещество электропроводно, не вытекает то, что оно – металл). Эта особенность импликации обуславливает два правила условно-категорического умозаключения.

1. Утверждать можно только от основания к следствию, т.е. во второй посылке утверждающего модуса должно утверждаться основание импликации (первой посылки), а в выводе – ее следствие. В противном случае из двух истинных посылок может вытекать ложный вывод. Например, в условно-категорическом умозаключении:

Если слово стоит в начале предложения, то его надо писать с большой буквы.

Слово «Москва» надо писать с большой буквы.

Слово «Москва» всегда стоит в начале предложения.

во второй посылке утверждалось следствие, а в выводе – основание (((а®в)Ùв)®а). Это утверждение от следствия к основаниюи является причиной ложного вывода при истинных посылках.

2. Отрицать можно только от следствия к основанию, т.е. во второй посылке отрицающего модуса должно отрицаться следствие импликации (первой посылки), а в выводе – ее основание. В противном случае из двух истинных посылок может вытекать ложный вывод. Например, в условно-категорическом умозаключении:

Если слово стоит в начале предложения, то его надо писать с большой буквы.

В данном предложении слово «Москва» не стоит в начале.

В данном предложении слово «Москва» не надо писать с большой буквы.

во второй посылке отрицается основание, а в выводе – следствие (((а®в)ÙØа)®Øв). Это отрицание от основания к следствиюи является причиной ложного вывода при истинных посылках.

Вспомним, что среди сложных суждений помимо импликации (а®в) есть также эквиваленция (а«в). Если в импликации всегда выделяется основание и следствие, то в эквиваленции нет ни того, ни другого, т.к. она представляет собой сложное суждение, обе части которого тождественны (эквивалентны) друг другу. Если первой посылкой умозаключения является не импликация, а эквиваленция, то такое умозаключение называется эквивалентно-категорическим.Например:

Если число четное, то оно делится без остатка на 2.

Число 16 - четное.

Число 16 делится без остатка на 2.

((а«в)Ùа)®в)

Если в условно-категорическом умозаключении два модуса правильных и два неправильных (см. выше), то в эквивалентно-категорическом умозаключении все четыре модуса являются правильными:

1. ((а«в)Ùа)®в

2. ((а«в)Ùв)®а

3. ((а«в)ÙØа)®Øв

4. ((а«в)ÙØв)®Øа

Читатель без труда сможет подобрать примеры для каждого из этих четырех модусов эквивалентно-категорического умозаключения.

Если обе посылки умозаключения представляют собой условные суждения, то это чисто условное умозаключение. Например:

Если вещество является металлом, то оно электропроводно.

Если вещество электропроводно, то его невозможно использовать в качестве изолятора.

Если вещество является металлом, то его невозможно использовать в качестве изолятора.

((а®в)Ù(в®с))®(а®с)

Резюме: Простым силлогизмом называется умозаключение, обе посылки и вывод которого являются простыми суждениями. Фигура силлогизма – это взаимное расположение его терминов, а модус – набор видов простых суждений, входящих в него. В разделительно-категорическом умозаключении первая посылка является дизъюнктивным суждением, а в условно-категорическом – импликативным. Как в простом силлогизме, так и в разделительно-категорическом и условно-категорическом умозаключениях истинность посылок не гарантирует истинности вывода, требуется также соблюдать определенные правила этих умозаключений. При нарушениях этих правил из истинных посылок могут вытекать ложные выводы.

Вопросы для самопроверки

1. Что такое простой силлогизм? Какова структура простого силлогизма? Что такое фигура простого силлогизма? Подумайте, почему возможно только четыре фигуры силлогизма? Как определить фигуру предложенного силлогизма?

2. Что такое модус простого силлогизма? Как определить модус предложенного силлогизма? Сколько модусов существует во всех четырех фигурах силлогизма? Что такое правильные и неправильные модусы? Сколько существует правильных модусов?

3. Каковы основные правила простого силлогизма? Приведите по два примера для ошибок: учетверение терминов, нераспределенность среднего термина в посылках, расширение большего термина, две отрицательные посылки.

4. Что такое разделительно-категорическое умозаключение? Какие модусы оно имеет? Каковы его правила? Какие ошибки возникают при их нарушении? Придумайте по одному примеру для каждой ошибки, возникающей при нарушении соответствующего правила.

5. Что такое условно-категорическое умозаключение? Какие модусы оно имеет? Каковы его правила? Какие ошибки возникают при их нарушении? Придумайте по два примера для каждой ошибки, возникающей при нарушении соответствующего правила.

Литература

1. Гетманова А. Д. Учебник по логике. – М.: Че Ро, 2000.

2. Гусев Д. А. Логика. Учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2004.

3. Гусев Д. А. Конспект лекций с задачами. Учебное пособие для вузов. –М.: Айрис Пресс, 2005.

4. Гусев Д. А. Логика. Учебное пособие. – М.: МПСИ, 2005.

5. Гусев Д. А. Тестовые задания и занимательные задачи по логике. – М.: МПСИ, 2003.

6. Ивин А.А. Логика. Учебное пособие. – М.: Знание, 1998.

7. Ивин А.А. Практическая логика. Задачи и упражнения. – М.: Просвещение, 1996.

8. Ивин А.А. Строгий мир логики. – М., 1988.

9. Краткий словарь по логике. – М., 1991.

10. Свинцов В. И. Логика. Элементарный курс для гуманитарных специальностей. – М., 1998.