Данное учебно-методическое пособие предназначено для студентов III курса специальности 280201 – «Охрана окружающей среды и рациональное использование природных ресурсов».
Многие направления профессиональной деятельности в области охраны окружающей среды и рационального использования природных ресурсов предполагают проведение статистической обработки различных результатов наблюдений.
Одним из способов обработки статистических данных является математическое моделирование, включающее в себя графическое представление статистических данных и установление математической модели функции распределения результатов наблюдений.
В практической работе последовательно излагаются основные теоретические положения и порядок выполнения работы, приводится список контрольных вопросов и требования к содержанию отчета.
Защита работы осуществляется по контрольным вопросам. К защите представляется отчет, аккуратно оформленный чернилами одного цвета. В тексте не допускается применять сокращения слов, кроме установленных ГОСТ 7.12–77.
Работа
УСТАНОВЛЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ
Цель работы: практически ознакомиться с порядком установления математической модели распределения погрешностей измерений для многократных наблюдений определения концентрации вредного вещества в окружающей среде.
Основные теоретические положения
Математическую обработку статистических данных выполняют в следующем порядке:
1. Определяют центр распределения погрешностей. При этом выбирают одну из четырех оценок, эффективность которой максимальна для данного класса распределения погрешностей:
1) определяют среднее арифметическое по формулам:
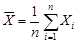 ; (1)
; (1)
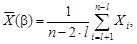 (2)
(2)
где β ∙n ≤ l ≤ β ∙n + 1; β = 0,05 или β = 0,1 для случая, когда с каждого конца вариационного ряда (ряд значений погрешностей, расположенных в порядке возрастания) исключают по l значений для получения более устойчивой оценки центра распределения погрешностей;
2) определяют медиану Ме – значение случайной величины погрешности, при котором Р(X < Ме) = Р(Х > Ме) = 1/2, по формулам:
если n – четное,
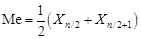 ; (3)
; (3)
если n – нечетное,
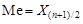 ; (4)
; (4)
3) определяют центр размаха по формуле
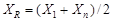 ; (5)
; (5)
4) определяют центр срединного размаха по формулам:
если n – кратно 4,
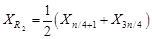 ; (6)
; (6)
если n – четное,
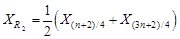 ; (7)
; (7)
если (n–1) – кратно 4,
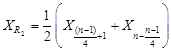 ; (8)
; (8)
если (n+1) – кратно 4,
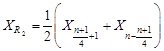 . (9)
. (9)
Наиболее эффективными оценками центра распределения погрешностей являются:
– для симметричных экспоненциальных распределений погрешностей при 0 < k < 0,45 – медиана Ме;
– для распределения погрешностей, близких к нормальному закону, при 0,45 ≤ k ≤ 0,67 – среднее арифметическое 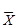 ;
; 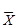 (0,05);
(0,05); 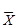 (0,1), занимающее медианное положение;
(0,1), занимающее медианное положение;
– для распределения погрешностей с крутыми спадами, близкими к законам равнопеременной плотности и арксинусоидальному, при 0,67 ≤ k < 1 – центр размаха ХR;
– для распределения погрешностей при 0,67 ≤ k < 1 – центр срединного размаха ХR2.
2. Определяют моменты распределения погрешностей. Формулы для определения начальных αk и центральных μk моментов и соотношения между ними приведены в табл. 1.
Таблица 1
Формулы для определения начальных и центральных моментов
| αк | μk | μk = f (αk) |
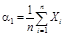 | 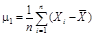 | 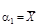 ; ; 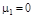 |
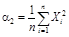 | 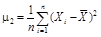 | μ2 = α2 – α12 |
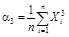 | 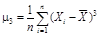 | μ3 = α 3 – 3 α 2 α 1 + 2 α 13 |
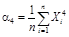 | 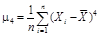 | μ4 = α4 – 4 α 3 α 1 + 6 α 2 α 12 – – 3 α 14 |
3. Определяют параметры рассеивания погрешностей. Несмещенную оценку дисперсии и среднего квадратического отклонения определяют по формулам:
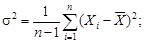 (10)
(10)
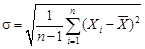 . (11)
. (11)
4. Определяют параметры островершинности распределения погрешностей. Эксцесс определяют по формуле
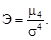 (12)
(12)
Коэффициент эксцесса определяют по формуле
γэ = μ4/σ4 + 3. (13)
Контрэксцесс определяют по формуле
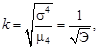 (14)
(14)
где 0 < k < 1.
5. Определяют границы промахов. Промахами (грубыми погрешностями) считают погрешности, отклонения которых от центра распределения существенно превышают значения, оправданные объективными условиями измерения, и для которых выполняются неравенства Хг— > Хi и Хг+ < Хi, где Хг— и Хг+ - границы промахов, определяемые из выражения
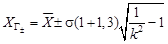 , (15)
, (15)
где 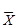 – центр распределения погрешностей, определенный в зависимости от значения k.
– центр распределения погрешностей, определенный в зависимости от значения k.
После исключения из выборки промахов повторяют вычисления по пп. 1–5.
6. Определяют параметры асимметрии распределения погрешностей. Коэффициент асимметрии распределения погрешностей определяют по формуле
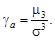 (16)
(16)
Среднее квадратическое отклонение коэффициента асимметрии определяют по формуле
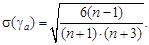 (17)
(17)
Распределение погрешностей симметрично, если выполняется условие
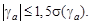 (18)
(18)
7. Определяют показатель формы распределения погрешностей. Показатель формы распределения погрешностей измерения связан с эксцессом Э функциональной зависимостью
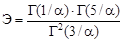 (19)
(19)
и определяется по графику зависимости показателя формы α от эксцесса Э, представленному на рис. 1.
8. Графически представляют статистические данные. Законы распределения погрешностей измерения и средств измерений определяют экспериментально на основании статистических данных.
Допустим, определяется закон распределения погрешности измерения или средства измерений при ручной обработке информации. Гистограмма (ступенчатый многоугольник, служащий для наглядного представления об эмпирическом распределении и оценки качества произведенного группирования), являющаяся ступенчатой аппроксимацией плотности вероятностей погрешностей, строится в следующем порядке:
1) значения погрешностей располагают в вариационный ряд Х1; Х2; …; Х S ; …; Хn, где Х S-1 ≤ ХS ≤ Х S+1;
|
|
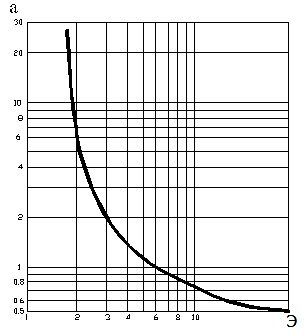
Рис. 1. Зависимость показателя формы α от эксцесса Э
2) определяют число интервалов группирования погрешностей, используя вычисленное значение контрэксцесса k:
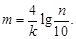 (20)
(20)
Значение m округляют до большего нечетного числа;
3) определяют ширину интервала группирования:
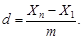 (21)
(21)
4) группируют погрешности по интервалам:
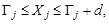 (22)
(22)
где Гj - левая граница j-го интервала группирования (j = 1, 2, …, m);
5) определяют вероятность рi попадания погрешностей в j-й интервал группирования:
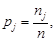 (23)
(23)
где j = 1, 2, …, m.
Сумма вероятностей по всем интервалам равна
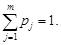 (24)
(24)
На каждом интервале, как на основании, строят прямоугольник, площадь которого равна вероятности этого интервала, высота – вероятности, деленной на ширину интервала. Масштаб графика выбирают таким образом, чтобы отношение высоты гистограммы к ее основанию составляло примерно 0,6.
Полигон (ломаную линию) распределения погрешностей строят, соединяя середины верхних сторон прямоугольников гистограммы. Гистограмме обычно отдают предпочтение, потому что ее площадь всегда равна объему выборки, а площадь под полигоном этим качеством не обладает.
Гистограмма или полигон может иметь не одну, а две или несколько вершин, наличие которых трудно объяснить случайными колебаниями. Тогда следует предположить, что вариационный ряд составлен при существенно разных условиях. В этом случае тщательно анализируют условия наблюдения.
9. Определяют информационные характеристики распределения погрешностей. Энтропийное значение погрешности определяют по формуле
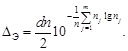 (25)
(25)
Энтропийный коэффициент, определяющий форму вершины распределения погрешностей, определяют по формуле
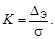 (26)
(26)
На основании вида гистограммы и полигона, а также сравнения оценок параметров и характеристик эмпирического распределения погрешностей: Э; γэ; k; γа; σ (γа); α с их критериальными значениями, приведенными в табл. 26 [5], выдвигают одну или несколько гипотез о виде математической модели эмпирического распределения погрешностей.
На основании гипотез последовательно производят вычисление теоретических плотностей распределения вероятностей погрешностей и теоретических частот следующим образом. Подставляют значения параметров табл. 26 [5] в математическую модель распределения погрешностей и, умножая полученные значения на ширину интервала группирования d, определяют плотность распределения вероятностей погрешности f (X) для значений Хj (i = 1, 2, …, m), равных серединам интервалов группирования. Теоретические частоты n¢i определяют в каждом интервале группирования, умножая вычисленные значения плотности распределения погрешностей f (X i) на объем выборки n.
После этого проверяют соответствие эмпирического распределения погрешностей выбранной математической модели. Проверку производят в зависимости от объема выборки. Для объемов выборок 50 > n > 15 проверку проводят по составному критерию, для объемов выборок 50 < n < 200 проверку на соответствие эмпирического распределения математической модели проводят по критерию Мизеса – Смирнова (ω2), для выборки с n > 100 рассчитывают критерий Пирсона (c2).
Составной критерий состоит из двух составляющих.
Критерий 1. Определяют значение отношения 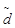 по формуле
по формуле
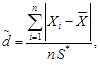 (27)
(27)
где S* - смещенная оценка среднего квадратического отклонения, вычисляемая по формуле
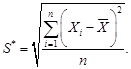 (28)
(28)
Распределение результатов наблюдений считают нормальным, если
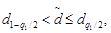 (29)
(29)
где 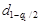 и
и 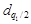 – квантили распределения, определяемые в соответствии с прил. 1 по n, q1/2 и (1 - q1/2), причем q1 – заранее выбранный уровень значимости критерия.
– квантили распределения, определяемые в соответствии с прил. 1 по n, q1/2 и (1 - q1/2), причем q1 – заранее выбранный уровень значимости критерия.
Критерий 2. Результаты наблюдений считают нормальными, если не более m разностей (Хi - 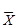 ) превзошло значение ZP/2 S, где ZP/2 – верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности Р/2; S – оценка среднего квадратического отклонения, вычисляемая по формуле
) превзошло значение ZP/2 S, где ZP/2 – верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности Р/2; S – оценка среднего квадратического отклонения, вычисляемая по формуле
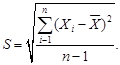 (30)
(30)
Значения Р определяют в соответствии с прил. 2 по выбранному уровню значимости q2 и числу результатов наблюдений n.
Если при проверке соответствия опытных данных теоретическим для критерия 1 выбран уровень значимости q1, а для критерия 2 – q2, то результирующий уровень значимости составного критерия равен q = q1 + q2. Если хотя бы один из критериев не соблюдается, то гипотеза о теоретическом распределении отвергается.
Вычисления критерия Мизеса – Смирнова проводят в следующем порядке.
Определяют значение ωn2 по формуле
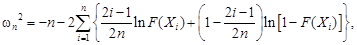 (31)
(31)
где Хi (i = 1, 2, …, n) – результат наблюдений, имеющий i-й номер в вариационном ряду Х1 ≤ Х2 ≤ … ≤ Хn; F (Xi) – значение функции теоретического распределения при значении аргумента Хi, равное
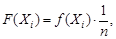 (32)
(32)
где f (Xi) – плотность вероятности функции распределения.
Результаты, полученные по формуле (31), сводят в табл. 2. Вычисления проводят с точностью до пяти значащих цифр, округляя окончательный результат до двух значащих цифр. Заполнив табл. 2, получают значение ωn2 путем суммирования чисел, занесенных в графу 10 табл. 2. Затем по прил. 3 находят значение функции α(ωn2), соответствующее вычисленному значению ωn2. Функция α(ωn2) представляет собой функцию распределения величины ωn2.
После этого задают уровень значимости α, равный 0,1 или 0,2. Если α(ωn2) ≥ (1 – α), то гипотезу о согласии эмпирического и теоретического распределений отвергают. Если α(ωn2) < (1 – α), то гипотезу принимают.
Если для нескольких математических моделей нет существенного расхождения с эмпирическим распределением погрешностей, то в качестве математической модели принимают ту из них, для которой получена наибольшая вероятность согласия.
Порядок выполнения работы
Студенты получают задание с исходными данными для расчета и установления математической модели распределения погрешностей измерений определения концентрации вредного вещества в окружающей среде. Работу выполняют в несколько этапов:
1. Изучают основные теоретические положения и выбирают одну из оценок центра распределения погрешностей;
2. Производят графическое построение математической модели распределения погрешностей и определяют ее характеристики;
3. Сравнивают экспериментальные и теоретические модели распределения погрешностей и выбирают закон распределения;
4. Производят проверку соответствия эмпирического распределения выбранной модели.
Пример
По данным многократных наблюдений концентрации вредных веществ выборка объемом n = 80 со значениями от 4,92 до 5,16.
На основании формул (1), (2), (11), (14), (15) определяют оценки параметров и характеристик эмпирического распределения погрешностей: 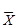 = 5,0168; σ = 0,045; k = 0,54; Хг— = 4,879; Хг+ = 5,155.
= 5,0168; σ = 0,045; k = 0,54; Хг— = 4,879; Хг+ = 5,155.
Значение 5,16 является промахом на основании (15), а поэтому после исключения его из вариационного ряда получили:
n = 79; 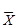 = 5,015; Ме = 5,020; Хг— = 4,893; Хг+ =5,1317;
= 5,015; Ме = 5,020; Хг— = 4,893; Хг+ =5,1317;
σ = 0,042; γа = -0,33; 1,5σ(γа) = 0,4; γэ = -0,14;
k = 0,59; Δ = 0,079; K = 1,87; m = 7 (6,07); d = 0,027.
Так как | γа | < 1,5 σ(γа), т.е. 0,33 < 0,4, эмпирическое распределение погрешностей считают симметричным и выбор математической модели осуществляют для симметричных функций.
Графическое представление эмпирического распределения погрешностей в виде гистограммы и полигона показано на рис. 2. Количество интервалов группирования значений выборки определяется по формуле (20)
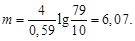
Полученное значение округляют до большего нечетного числа m = 7.
На основании сравнения оценок параметров и характеристик эмпирического распределения погрешностей с их числовыми значениями для математических моделей табл. 26 [5]) выбирают две теоретические функции – нормальную (рис. 2, б) и треугольную (рис. 2, в) в качестве аппроксимирующих данное эмпирическое распределение погрешностей для дальнейшей проверки их по критериям согласия. Вычисляют значения теоретических вероятностей и заносят данные в табл. 3.
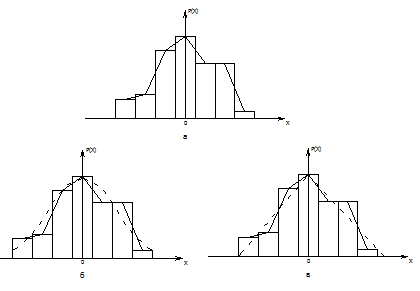 Рис. 2. Графическое представление эмпирического распределения
Рис. 2. Графическое представление эмпирического распределения
Таблица 3
Расчетные данные
| Номер интервала | Середина интервала | Эмпирическая частость | Вероятность | Теоретическая частость | ||
| Нормальная функция | Треугольная функция | Нор- мальная функция | Тре- угольная функция | |||
| 4,9336 | 0,04 | 0,055 | 3,13 | 4,37 | ||
| 4,9607 | 0,112 | 0,125 | 8,85 | 9,85 | ||
| 4,9879 | 0,209 | 0,194 | 16,51 | 15,32 | ||
| 5,0150 | 0,257 | 0,263 | 20,32 | 20,8 | ||
| 5,0421 | 0,209 | 0,194 | 16,51 | 15,32 | ||
| 5,0693 | 0,112 | 0,125 | 8,84 | 9,85 | ||
| 5,0963 | 0,04 | 0,055 | 3,13 | 4,37 |
Проверку согласия эмпирического распределения с выбранными теоретическими функциями (нормальной и треугольной) проводят по критерию ω2:
(ωn2)норм = 3,87; (ωn2)треуг = 1,07.
После этого задают уровень значимости q = 0,1. По прил. 3 находят значение функции α (ωn2), соответствующее вычисленному значению ωn2. Значения ωn2 в прил. 3 ограничены значением 2,5. При (ωn2)норм > 2,5 значение функции α(ωn2)норм > 0,95 и стремится к единице. При (ωn2)треуг = 1,07 α(ωn2)треуг будет равно 0,673. При заданном уровне значимости q = 0,1 α (ωn2)треуг = 0,673 >
> (1 - 0,1).
Таким образом, принимают гипотезу о законе распределения Симпсона. Математическая модель эмпирического распределения погрешностей имеет вид
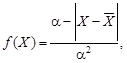
где α = σ 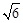 .
.
Содержание отчета
1. Цель работы.
2. Основные теоретические положения.
3. Исходные данные.
4. Результаты расчета и их анализ.
5. Выводы по работе.
6. Список использованной литературы.
Контрольные вопросы
1. Какие характеристики могут быть выбраны в качестве оценки центра распределения погрешностей?
2. Перечислите основные этапы статистической обработки данных.
3. Каким параметром характеризуется рассеивание погрешностей?
4. Каким параметром характеризуется асимметрия распределения погрешностей?
5. Приведите особенности графического представления статистических данных.
6. Приведите характеристику составного критерия.
7. Приведите характеристику критерия Мизеса – Смирнова.
Список литературы
1. Сергеев А.Г. Метрология: Учеб. пособие для вузов. – М.: Логос, 2000. – 408 с.
2. Крылова Г.Д. Основы стандартизации, сертификации, метрологии: Учеб. для вузов. – М.: ЮНИТИ-ДАНА, 1999. – 711 с.
3. Тартаковский Д.Ф., Ястребов А.С. Метрология, стандартизация и технические средства измерений: Учеб. для вузов. – М.: Высш. шк., 2001. – 205 с.
4. Рабинович С.Г. Погрешности измерений. – М.: Энергия. Ленингр. отд. – 1978. – 261 с.
5. Артемьев Б.Г., Голубев С.М. Справочное пособие для работников метрологических служб. Кн. 1. – М.: Изд-во стандартов. – 1990. – 960 с.
ПРИЛОЖЕНИЯ
Приложение 1
Квантили распределения
| n | (q1/ 2) ∙ 100 % | (1 – q1/2) ∙ 100 % | ||
| 1 % | 5 % | 96 % | 99 % | |
| 0,9137 | 0,8884 | 0,7236 | 0,6829 | |
| 0,9001 | 0,8768 | 0,7304 | 0,6950 | |
| 0,8901 | 0,8686 | 0,7360 | 0,7040 | |
| 0,8826 | 0,8625 | 0,7404 | 0,7110 | |
| 0,8769 | 0,8578 | 0,7440 | 0,7167 | |
| 0,8722 | 0,8540 | 0,7470 | 0,7216 | |
| 0,8682 | 0,8508 | 0,7496 | 0,7256 | |
| 0,8648 | 0,8481 | 0,7518 | 0,7291 | |
| 0,8619 | 0,8458 | 0,7538 | 0,7323 | |
| 0,8594 | 0,8438 | 0,7557 | 0,7353 | |
| 0,8572 | 0,8420 | 0,7576 | 0,7382 | |
| 0,8552 | 0,8403 | 0,7594 | 0,7410 | |
| 0,8533 | 0,8386 | 0,7612 | 0,7438 | |
| 0,8514 | 0,8370 | 0,7630 | 0,7465 | |
| 0,8496 | 0,8354 | 0,7647 | 0,7492 | |
| 0,8478 | 0,8338 | 0,7664 | 0,7519 | |
| 0,8460 | 0,8323 | 0,7681 | 0,7545 | |
| 0,8443 | 0,8308 | 0,7698 | 0,7571 |
Приложение 2
Значения вероятности Р в зависимости от n и q2
| n | m | q2 ∙ 100 % | ||
| 1 % | 2 % | 5 % | ||
| 0,98 | 0,98 | 0,96 | ||
| 11 – 14 | 0,99 | 0,98 | 0,97 | |
| 15 – 20 | 0,99 | 0,99 | 0,98 | |
| 21 – 22 | 0,98 | 0,97 | 0,96 | |
| 23 – 27 | 0,98 | 0,98 | 0,97 | |
| 28 – 32 | 0,99 | 0,98 | 0,98 | |
| 33 – 35 | 0,99 | 0,98 | 0,98 | |
| 36 – 49 | 0,99 | 0,99 | 0,98 | |
| 50 – 53 | 0,98 | 0,97 | 0,96 | |
| 0,98 | 0,98 | 0,96 | ||
| 55 – 60 | 0,98 | 0,98 | 0,97 | |
| 61 – 69 | 0,99 | 0,98 | 0,98 | |
| 70 – 83 | 0,99 | 0,99 | 0,98 | |
| 84 – 90 | 0,98 | 0,97 | 0,96 | |
| 91 – 100 | 0,98 | 0,99 | 0,96 |
Приложение 3
Значение функции α (ωn2) при втором знаке после запятой ωn2
| Значение ωn2 | ||||||||||
| 0,0 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 0,1 | 0,000 | 0,000 | 0,000 | 0,000 | 0,001 | 0,001 | 0,002 | 0,003 | 0,005 | 0,007 |
| 0,2 | 0,010 | 0,013 | 0,016 | 0,020 | 0,025 | 0,030 | 0,035 | 0,041 | 0,048 | 0,055 |
| 0,3 | 0,062 | 0,070 | 0,078 | 0,086 | 0,095 | 0,104 | 0,113 | 0,122 | 0,132 | 0,141 |
| 0,4 | 0,151 | 0,161 | 0,171 | 0,181 | 0,192 | 0,202 | 0,212 | 0,222 | 0,233 | 0,243 |
| 0,5 | 0,253 | 0,263 | 0,274 | 0,284 | 0,294 | 0,304 | 0,313 | 0,323 | 0,333 | 0,343 |
| 0,6 | 0,352 | 0,361 | 0,371 | 0,380 | 0,389 | 0,398 | 0,407 | 0,416 | 0,424 | 0,433 |
| 0,7 | 0,441 | 0,449 | 0,458 | 0,466 | 0,474 | 0,482 | 0,489 | 0,497 | 0,504 | 0,512 |
| 0,8 | 0,519 | 0,526 | 0,533 | 0,540 | 0,547 | 0,554 | 0,560 | 0,567 | 0,573 | 0,580 |
| 0,9 | 0,586 | 0,592 | 0,598 | 0,604 | 0,610 | 0,615 | 0,621 | 0,627 | 0,632 | 0,637 |
| 1,0 | 0,643 | 0,648 | 0,653 | 0,658 | 0,663 | 0,668 | 0,673 | 0,677 | 0,682 | 0,687 |
| 1,1 | 0,691 | 0,696 | 0,700 | 0,704 | 0,709 | 0,713 | 0,717 | 0,721 | 0,725 | 0,729 |
| 1,2 | 0,732 | 0,736 | 0,740 | 0,744 | 0,747 | 0,751 | 0,754 | 0,758 | 0,761 | 0,764 |
| 1,3 | 0,768 | 0,771 | 0,774 | 0,777 | 0,780 | 0,783 | 0,786 | 0,789 | 0,792 | 0,795 |
| 1,4 | 0,798 | 0,800 | 0,803 | 0,806 | 0,809 | 0,811 | 0,814 | 0,816 | 0,819 | 0,821 |
| 1,5 | 0,824 | 0,826 | 0,828 | 0,831 | 0,833 | 0,835 | 0,837 | 0,839 | 0,842 | 0,844 |
| 1,6 | 0,846 | 0,848 | 0,850 | 0,852 | 0,854 | 0,856 | 0,858 | 0,859 | 0,861 | 0,863 |
| 1,7 | 0,865 | 0,867 | 0,868 | 0,870 | 0,872 | 0,873 | 0,875 | 0,877 | 0,878 | 0,880 |
| 1,8 | 0,881 | 0,883 | 0,884 | 0,886 | 0,887 | 0,889 | 0,890 | 0,892 | 0,893 | 0,894 |
| 1,9 | 0,896 | 0,897 | 0,898 | 0,900 | 0,901 | 0,902 | 0,903 | 0,905 | 0,906 | 0,907 |
| 2,0 | 0,908 | 0,909 | 0,910 | 0,912 | 0,913 | 0,914 | 0,915 | 0,916 | 0,917 | 0,918 |
| 2,1 | 0,919 | 0,920 | 0,921 | 0,922 | 0,923 | 0,924 | 0,925 | 0,926 | 0,927 | 0,928 |
| 2,2 | 0,929 | 0,929 | 0,930 | 0,931 | 0,932 | 0,933 | 0,934 | 0,934 | 0,935 | 0,936 |
| 2,3 | 0,937 | 0,938 | 0,938 | 0,939 | 0,940 | 0,941 | 0,941 | 0,942 | 0,943 | 0,943 |
| 2,4 | 0,944 | 0,945 | 0,945 | 0,946 | 0,947 | 0,947 | 0,948 | 0,949 | 0,949 | 0,950 |
Содержание
Введение................................ 3
Работа. Установление математической модели распределения по-
грешностей................................. 4
Список литературы.......................... 19
ПРИЛОЖЕНИЯ........................... 20
Приложение 1............................. 20
Приложение 2............................. 21
Приложение 3............................. 22
 |
Редактор Н.А. Бачурина
Компьютерная верстка: Т.С. Камыгина
Лицензия А № 001633 от 02 февраля 2004 г.
 |
Сдано в набор 08.08.05. Подписано к печати 06.09.05 г.
Тир. 25. Уч.-изд. л. 1,03. Формат 60´84 1/16. Усл. печ. л. 1,63.
Гарнитура Таймс. Зак. .
 ГОУ ВПО Череповецкий государственный университет
ГОУ ВПО Череповецкий государственный университет
162600, г. Череповец, пр. Луначарского, 5.
Таблица 2
Значения промежуточных вычислений
| Номер наблюдения в вариационном ряду | 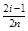 | F (Xi) | ln(3) | (2) ∙ (4) | 1 – (2) | 1 – (3) | Įn(7) | (6) ∙ (8) | (5) + (9) |
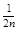 | F (X1) | ln F (X1) | 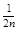 ´ ´ ln F (X1) ´ ´ ln F (X1) | 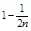 | 1 - F (X1) | ln [1 - F (X1)] | 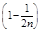 ´ ´ ln [1 - F (X1)] ´ ´ ln [1 - F (X1)] | 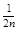 ln F (X1) + ln F (X1) + 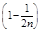 ´ ´ ln [1 - F (X1)] ´ ´ ln [1 - F (X1)] | |
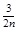 | F (X2) | ln F (X2) | 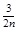 ´ ´ ln F (X2) ´ ´ ln F (X2) | 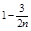 | 1 - F (X2) | ln [1 - F (X2)] | 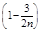 ´ ´ ln [1 - F (X2)] ´ ´ ln [1 - F (X2)] | 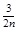 ln F (X2) + + ln F (X2) + + 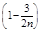 ln [1 - F (X2)] ln [1 - F (X2)] | |
| ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ |
| i | 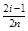 | F (Xi) | ln F (Xi) | 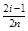 ´ ´ ln F (Xi) ´ ´ ln F (Xi) | 1 - 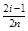 | 1 - F (Xi) | ln [1 - F (Xi)] | 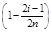 ´ ´ ln [1 - F (Xi)] ´ ´ ln [1 - F (Xi)] | 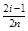 ln F (Xi) + + ln F (Xi) + + 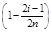 ln [1 - F (Xi)] ln [1 - F (Xi)] |
| ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ | ∙ |
| n | 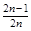 | F (Xn) | ln F (Xn) | 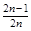 ´ ´ ln F (Xn) ´ ´ ln F (Xn) | 1 - 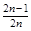 | 1 - F (Xn) | ln [1 - F (Xn)] | 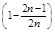 ´ ´ ln [1 - F (Xn)] ´ ´ ln [1 - F (Xn)] | 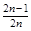 ln F (Xn) + ln F (Xn) + 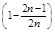 ´ ´ ln [1 - F (Xn)] ´ ´ ln [1 - F (Xn)] |
 Примечание. Цифры в скобках в головке табл. 2, например (3), (4), обозначают номера граф, из которых надо брать числа для вычисления. Например, ln(3) означает, что надо вычислить натуральный логарифм числа, находящегося в графе 3.
Примечание. Цифры в скобках в головке табл. 2, например (3), (4), обозначают номера граф, из которых надо брать числа для вычисления. Например, ln(3) означает, что надо вычислить натуральный логарифм числа, находящегося в графе 3.
