Процесс доказательства методом резолюций.

Используется доказательство методом от противного. Отрицание заключения принимается в качестве дополнительной посылки.

1. Все посылки и отрицания заключения привести к нормальной форме. Для этого используются следующие равносильности:

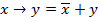
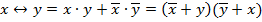
При необходимости применяются законы де Моргана:

.

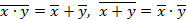2. Все полученные в 1–м пункте дизъюнкты записываются с новой строки (включая отрицание заключения). В результате получается последовательность формул или последовательность дизъюнктов.

3. В полученной последовательности находим любые две формулы, в одной из которых находится атом, а в другой отрицание атома. Положение атомов в формуле роли не играет. Эти две формулы соединяем с помощью правила резолюций и получаем новую формулу без этого атома.

4. Затем ищут следующую пару формул аналогичным образом, в одной из которых атом, а в другой отрицание, и соединяют эти две формулы с помощью правила резолюций и т.д.

Аналогичным образом продолжают до тех пор, пока не появится пустой дизъюнкт □, который и выражает противоречие.

Преимущества использования правила резолюций:

1) В этом методе используется лишь одно правило – это правило резолюций. Не надо запоминать многочисленные правила вывода и теоремы классического исчисления высказываний.

2) В процессе доказательства не надо использовать различные равносильности для проведения простых преобразований.

3) Метод прост в реализации.

Замечание. На основе этого правила разработан язык логического программирования – Пролог.

Пример. 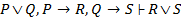. Доказать выводимость.

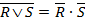
1) ; ;

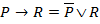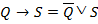2) 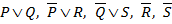– гипотезы

Дизъюнкты: 1. ;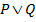

2. ;

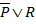3. ;

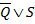4. ;

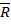5. ;

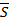3) 6. 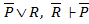(2, 4)

7. 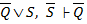(3, 5)

8. 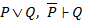(1, 6)

9. 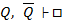– ложь.

При практической реализации этого метода, несмотря на простоту метода доказательства, может возникнуть ряд проблем. Последовательность может содержать большое количество формул. Возникает проблема, какие формулы соединить с помощью правила резолюции и как быстрее достичь цели. Для решения этих проблем разработаны специальные методики поиска.

5. ЛОГИКА ПРЕДИКАТОВ

5.1. Определение предиката

Понятие предиката обобщает понятие высказывания, а логика предикатов представляет собой дальнейшее развитие логики высказываний.

Предикат – предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить истинно оно или ложно. Дадим определение предиката.

Определение 1. n–местным предикатом, заданным на множестве М₁´М₂´…´М_n называется выражение, содержащее n переменных x₁, х₂, ..., х_n, которое становится высказыванием при подстановке вместо этих переменных элементов а₁, а₂, ..., а_n, из множеств М₁, М₂, ..., М_n соответственно.

Предикаты обозначаются как Р(х₁, х₂, ..., х_n) и пред­ставляют собой отображения Р: М₁´М₂´…´М_n 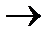{0,1}. То есть, упорядоченному набору элементов (а₁, а₂, ..., а_n) из множества М₁´…´М_n ставится в соответствие один из элементов множества {0,1}, причем 0, если Р(а₁, а₂, ..., а_n) – ложное высказывание и 1, если истинное. Переменные х₁, х₂, ..., х_n называются предметными, а элементы из множеств М₁, М₂, …, М_n, которые эти переменные пробегают – конкретными предметами. Местностью предиката называется число различных аргу­ментов, от которых зависит предикат. Предикат является функцией многих переменных.

Примеры

1. Предложение "х – четное число" представляет собой од­номестный предикат, заданный на множестве целых чисел, то есть Р: Z®{0, 1}. Областью определения предиката Р является множе­ство целых чисел Z, областью значений – множество {0, 1}.

2. Отношения "х < у" и "х делится на у"представляют собой двуместные предикаты, заданные на множествах R´R и Z´Z соответственно.

Определение 2. Множеством истинности предиката Р(х₁, х₂, ..., х_n), заданного на множестве М₁´М₂´…´М_n, называется совокупность таких упорядоченных наборов элементов (а₁, а₂, ..., а_n) из М₁´М₂´…´М_n, для которых высказывание Р(а₁, а₂, ..., а_n) является истинным.

Обозначение: P⁺ ={(а₁, а₂, ..., а_n): l( Р(а₁, а₂, ..., а_n)) =1}.

Примеры.

1. Множеством истинности двухместного предиката Р(х, у):"х делится на у", заданного на множестве М´М,
где М = {1, 2, 3, 4, 5, 6}, является следующее множество Р⁺ = {(1,1), (2,1), (3,1), (4,1), (5,1), (6,1), (4, 2), (6, 2), (6,3)}.

2. Множество истинности двуместного предиката Р(х,y): "x < у", заданного на множестве М₁´М₂, где М₁ = {1, 2, 3}, М₂ = {2, 4, 6}, равно P⁺ = {(1,2), (1,4), (1,6), (2,4), (2,6), (3,4), (3,6)}.

Определение 3.Два предиката Р(х₁, х₂, ..., х_n) и Q(х₁, х₂, ..., х_n), за­данные на одном и том же множестве М₁´М₂´…´М_n, называются равносильными, если оба предиката принимают истинные значения на одних и тех же наборах (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, то есть, если Р⁺= Q⁺. Предикат Q(х₁, х₂, ..., х_n), заданный на множестве М₁´М₂´…´М_n называется следствием предика­та Р(х₁, х₂, ..., х_n), заданного на том же множестве, если он становится истинным высказыванием при всех значениях переменных х₁, х₂, ..., х_n из соответствующих множеств М₁, М₂, ..., М_n, при кото­рых истинным высказыванием становится предикат Р(х₁, х₂, ..., х_n), то есть, если .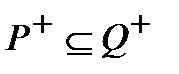

5.2. Логические операции над предикатами

Определение 4. Отрицанием предиката Р(х₁, х₂, ..., х_n), заданного на множестве М₁´М₂´…´М_n, называется новый предикат 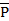(х₁, х₂, ..., х_n), заданный на том же множестве, который становится истинным высказыванием при таких значениях (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, при которых Р(а₁, а₂, ..., а_n) является ложным высказыванием и становится ложным высказыванием, если Р(а₁, а₂, ..., а_n) является истинным высказыванием.

Например, отри­цанием одноместного предиката Р(х): "х делится на 3", заданного на множестве М = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} будет предикат 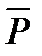: "х не делится на 3". Множествами истинности предикатов Р и 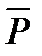яв­ляются следующие множества Р⁺= {0, 3, 6, 9}, ( 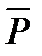)⁺ = {1, 2, 4, 5, 7, 8}.

Множество истинности предиката 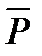является дополнением множества Р⁺_,то есть 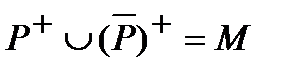( M – область определения предиката).

Определение 5. Конъюнкцией двух n–местных предикатов Р(х₁, х₂, ..., х_n) и Q(х₁, х₂, ..., х_n), заданных на множестве М₁´М₂´…´М_n, называется новый n–местный предикат Р(х₁, х₂, ..., х_n) Q(х₁, х₂, ..., х_n), который становится истинным высказыванием только для таких элементов (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, для которых Р(а₁, а₂, ..., а_n) и Q(а₁, а₂, ..., а_n) являются истинны­ми высказываниями.

Определение 6. Дизъюнкцией двух n–местных предикатов Р(х₁, х₂, ..., х_n) и Q(х₁, х₂, ..., х_n), заданных на множестве М₁´М₂´…´М_n, называется новый n–местный предикат Р(х₁, х₂, ..., х_n) Ú Q(х₁, х₂, ..., х_n), который становится ложным высказыванием только для таких элементов (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, для которых Р(а₁, а₂, ..., а_n) и Q(а₁, а₂, ..., а_n) являются ложными высказываниями.

Определение 7. Импликациейдвух n–местных предикатов Р(х₁, х₂, ..., х_n) и Q(х₁, х₂, ..., х_n), заданных на множестве М₁´М₂´…´М_n, называется новый n–местный предикат Р(х₁, х₂, ..., х_n) 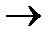Q(х₁, х₂, ..., х_n), который становится ложным высказыванием только для таких элементов (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, для которых Р(а₁, а₂, ..., а_n) является истинным высказыванием, а Q(а₁, а₂, ..., а_n) является ложным. В остальных случаях – истинным.

Определение 8. Эквивалентностью двух n–местных предикатов Р(х₁, х₂, ..., х_n) и Q(х₁, х₂, ..., х_n), заданных на множестве М₁´М₂´…´М_n, называется новый n–местный предикат Р(х₁, х₂, ..., х_n) 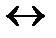Q(х₁, х₂, ..., х_n), который становится истинным высказыванием только для таких элементов (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, для которых высказывания Р(а₁, а₂, ..., а_n) и Q(а₁, а₂, ..., а_n) ли­бо одновременно являются истинными, либо ложными. В остальных случаях – ложным.

Если предикаты Р(х₁, х₂, ..., х_n) и Q(y₁, y₂, ..., y_m) заданы на разных множествах, то в результате применения операций конъюнк­ции, дизъюнкции, импликации и эквивалентности к этим предика­там, получим (n + m – k)–местный предикат, где k – число переменных, общих для обоих предикатов.

Кванторные операции

Кроме операций отрицания, конъюнкции, дизъюнкции, им­пликации и эквивалентности в логике предикатов имеются две кванторные операции: квантор всеобщности( 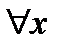) и существования( 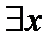). Если Р(х) одноместный предикат, заданный на некотором множестве М, то в результате применения кванторов к предикату Р(х) получим новые предикаты 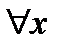P(x) и 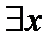Р(х), означающие соот­ветственно "все х из М обладают свойством Р"и "некоторые х из М обладают свойством Р".

Пример 1.Пусть Р(х) одноместный предикат "х делится на 7", за­данный на множестве целых чисел Z. Применяя к этому предикату кванторы получим следующие предикаты: "все х из Z делятся на число 7" и "существуют х из Z, которые делятся на число 7". То есть, в результате применения кванторов ( 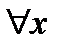) и ( 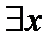) к одномест­ному предикату Р(х)получили высказывания, причем первое из них ложное, а второе – истинное. Высказывания являются нульместными предикатами.

Применение кванторов к предикатам понижает местность исходного предиката на единицу. Если Р(х₁, х₂, ..., х_n) n–местный предикат, то в результате применения кванторов получим новые предикаты Q(х₂, ..., х_n)= 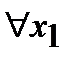Р(х₁, х₂, ..., х_n), R(х₂, ..., х_n)= 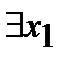Р(х₁, х₂, ..., х_n), которые зависят только от переменных х₂, х₂, ..., х_n,то есть являются (n – 1)–мест­ными предикатами.

Предметная переменная, которая связывается квантором, то есть входит в предикат и в квантор, называется связанной. Предметная переменная, не связанная никаким квантором, называется свободной переменной.

Пример 2.Пусть Р(х, y)двухместный предикат, заданный неравенством "х² + у² 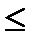1" на множестве R´R. Множеством истинности преди­ката Р(х, y)является множество всех точек координатной плоскости, расположенных внутри окружности радиуса 1, включая точки ок­ружности. Найдем множества истинности предикатов Q(y)= x P(x, y), R(x)= 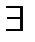у Р(х, у), S = x 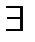y P(x, y). Множеством истинно­сти предиката Q(y)является множество таких у, для которых данное неравенство выполняется при любых х из R. Однако таких у не су­ществует. Следовательно, множество истинности предиката Q не со­держит ни одного элемента, то есть Q⁺ =Æ. Множеству истин­ности предиката R(x)принадлежат все такие х, для которых можно найти число у, удовлетворяющее данному неравенству. Такие зна­чения х лежат в промежутке [–1, 1]. Следовательно, этот промежуток и будет множеством истинности предиката R. Предикат S – нульместный, то есть является высказыванием. В высказывании S говорится, что для любых х можно найти такое у, для которой выполняется данное неравенство. Однако это не верно. Например, для х,лежащих вне отрезка [–1, 1], такое у не существует. Тогда S – ложное выска­зывание.

5.3. Теоретико–множественный смысл предикатов

При определении множества истинности предиката, составленного из нескольких предикатов при помощи логических связок, можно воспользоваться соотношениями для их множеств истинности. Для двух n–местных предикатов Р(х₁, х₂, ..., х_n) и Q(х₁, х₂, ..., х_n) задан­ных на множестве М₁´М₂´…´М_n, верны следующие соотношения для их множеств истинности:

1) множество истинности отрицания предиката Р равно дополнению множества истинности этого предиката, то есть ;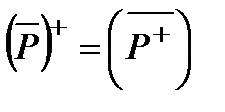

2)множество истинности конъюнкции двух предикатов Р и Q рав­но пересечению множеств истинности Р⁺ и Q⁺, то есть ;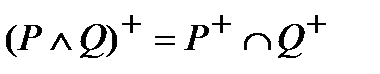

3) множество истинности дизъюнкции двух предикатов Р и Q рав­но объединению множеств истинности Р⁺ и Q⁺, то есть ;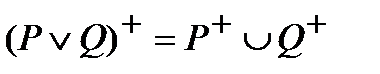

4) множество истинности импликации двух предикатов Р и Q равно ;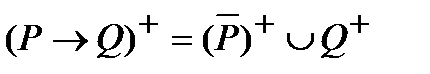

5) множество истинности эквивалентности двух предикатов Р и Q равно .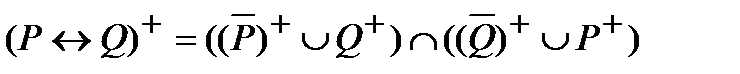

Пример. Пусть предикаты Р(х):"х кратно двум" и Q(x): "х кратно трем", заданы на множестве М = {1, 2, 3, 4, 5, 6, 7, 8}. Их множествами истинности являются следующие множества: Р⁺ = {2, 4, 6, 8}, Q⁺ = {3, 6}. Тогда, по соотношениям (1)–(5) получим

а) 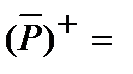{1, 3, 5, 7}, 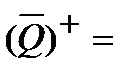{l, 2, 4, 5, 7, 8};

б) 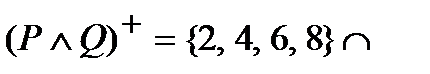{3, 6} = {6};

в) 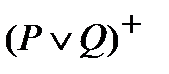= {2, 4, 6, 8} {3,6}= {2, 3, 4, 6, 8};

г) 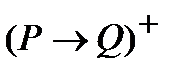={1, 3, 5, 7} {3,6} ={1, 3, 5, 6, 7};

д) 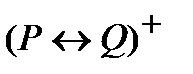={1, 3, 5, 6, 7} {1, 2, 4, 5, 6, 7, 8}= {1,5,6,7}.

5.4. Классификация предикатов

Определение 9.Предикат Р(х₁, х₂, ... х_n), заданный на множестве М₁´М₂´…´М_n, называется тождественно истинным, если для всех элементов (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n высказывания Р(а₁, а₂, ..., а_n) будут истинными и тождественно ложным, если для всех элементов (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, выска­зывания Р(а₁, а₂, ..., а_n) будут ложными. Предикат Р(х₁, х₂, ... х_n), за­данный на множестве М₁´М₂´…´М_n, называется выполнимым, если существует хотя бы один элемент (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n, для которого высказывание Р(а₁, а₂, ..., а_n) будет ис­тинным и опровержимым, если хотя бы для одного элемента (а₁, а₂, ..., а_n) из множества М₁´М₂´…´М_n высказывание Р(а₁, а₂, ..., а_n) будет ложным.

В соответствии с классификацией предикатов истинность нульместных предикатов, содержащих кван­торы, можно определить следующим образом. Высказывание "x P(x) будет истинным, если предикат Р(х)является тождественно истинным предикатом. В противном случае – ложным. Высказыва­ние $х Р(х) будет истинным, если предикат Р(х) – является выпол­нимым и будет ложным в противном случае.

5.5. Формулы логики предикатов.
Равносильность формул

Определение формулы логики предикатов имеет индуктивный ха­рактер. Сначала задается алфавит символов, из которых составляются формулы:

– предметные переменные: х, у, z, x_i, y_i, z_i ( );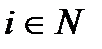

– нульместные предикатные переменные: Р, Q, R, Р_i, Q_i, R_i,

(i 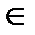N);

– n–местные ( 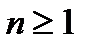) предикатные переменные: Р(, ..., ), Q(, ..., ), R(, ..., ), Р_i(, ..., ), Q_i(, ..., ), R_i(, ..., ) (i 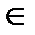N) с указанием числа свободных мест в них;

– символы логических операций: ;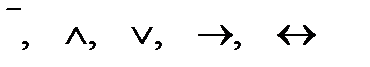

– кванторы: ", $;

– вспомогательные символы: (, ) – скобки; , – запятая.

Определение 10.(формулы логики предикатов).

1. Каждая нульместная предикатная переменная есть формула.

2. Любой n–местный предикат Р(х₁, х₂, ..., х_n) есть формула.

3. Если F, G – формулы, не содержащие предметных перемен­ных, которые связаны квантором в одной формуле и свободны в другой, то выражения ( 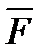), (F Ù G), (F Ú G), (F ® G ), (F « G) также являются формулами.

4. Если F формула, а х – предметная переменная, входящая сво­бодно в F, то выражения "x F(x) и $x F(x) также являются формулами.

5. Никаких других формул в логике предикатов нет.

Формулы, в которых нет свободных переменных, называются замкнутыми, а формулы, содержащие свободные переменные, – открытыми.

Из определения формулы логики предикатов следует, что все фор­мулы алгебры высказываний являются также формулами логики предикатов.

Определение 11.Две формулы F и G называются равносильными, если при подстановке в эти формулы вместо предикатных перемен­ных конкретных предикатов, а вместо предметных переменных конкретных элементов, эти формулы преобразуются в высказывания с одинаковыми логическими значениями, то есть либо оба в ис­тинные высказывания, либо оба в ложные.

Все основные равно­сильности логики высказываний верны также и для формул логики предикатов. Кроме них, в логике предикатов имеются равносильности, связанные с кванторами:

1. Законы отрицания: , .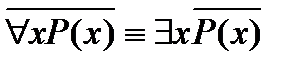

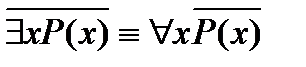2. Законы дистрибутивности:

;

.

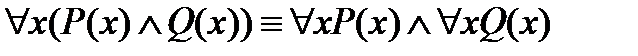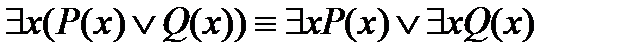3.Если предикат Q не зависит от переменной х, то верны сле­дующие законы:

, ;

, .

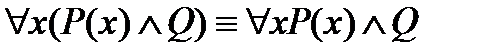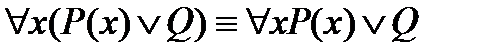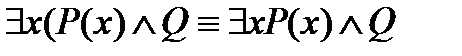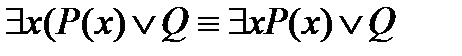4. Законы переименования связанных переменных:

, .

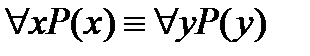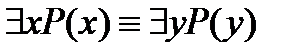5.Законы перестановки кванторов:

, .

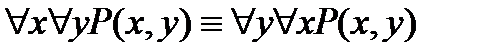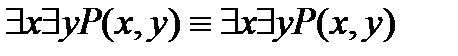5.6. Классификация формул логики предикатов

Определение 12.Формула F логики предикатов называется выпол­нимой (опровержимой) на множестве М, если можно найти такие конкретные предикаты, заданные на том же множестве, при подста­новке которых вместо предикатных переменных, она преобразуется в выполнимый (опровержимый) предикат. Формула логики преди­катов называется тождественно истинной (тождественно лож­ной) на множестве М, если при подстановке вместо предикатных пе­ременных любых конкретных предикатов, заданных на этом же множестве, она преобразуется в тождественно истинный (тождест­венно ложный) предикат. Формула логики предикатов называется тавтологией (противоречием), если при подстановке вместо преди­катных переменных любых конкретных предикатов, заданных на любом множестве, она преобразуется в тождественно истинный (тождественно ложный) предикат.

Критерием равносильности формул F и G является тавтологичность формулы (F« G).

Пример 1.Вычислить значение формулы 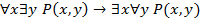, если предикат 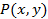имеет значение 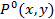– «число x меньше числа y» и определен на множестве 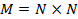, N= .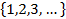

Так как при указанном значении предиката 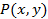высказывание 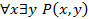означает утверждение, что «для любого натурального числа x найдется натуральное число y, большее числа x», то это высказывание истинно. Высказывание 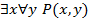означает утверждение, что «существует натуральное число x, которое меньше любого натурального числа y». Это высказывание ложно. Поэтому получаем, что исходная формула ложна.

Пример 2. Доказать, что формула 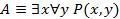выполнима.

Для доказательства выполнимости формулы A достаточно найти область определения двухместного предиката 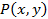и такое его значение, что в этой области формула принимает истинные значения. Такой областью определения предиката, в частности, будет множество 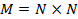. Действительно, если 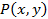- предикат «y:x», то формула A тождественно истинна в области М, и, следовательно, выполнима в этой области. Однако, если в качестве предиката 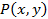взять предикат «y<x», то формула A будет тождественно ложной в области М и, следовательно, невыполнимой в области М. при этом ясно, что формула A не общезначима.

Пример 3. Доказать, что формула 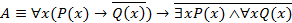является общезначимой.

Считая, что формула A определена на любой области M, проведем равносильные преобразования:

.

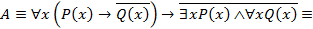
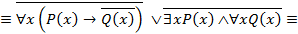
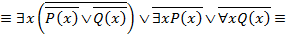
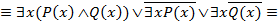
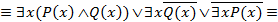
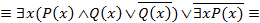
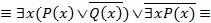
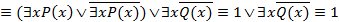То есть формула A тождественно истинна для любых одноместных предикатов 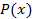и 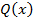и в любой области.

Пример 4. Доказать, что формула 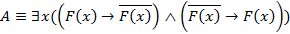тождественно ложна.

Так как формула 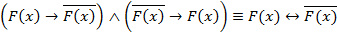, а формула 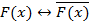, очевидно, тождественно ложна, то ложна и формула A.

Определение 13.Формула F', равносильная F, называется ее при­веденной формой, если F' из логических связок содер­жит только отрицание, конъюнкцию и дизъюнкцию, а отрицание относится только к предикатным переменным и к высказываниям. Предваренной нормальной формой (ПНФ) фор­мулы F называется такая ее приведенная форма, в которой все кванторы вынесены в начало формулы, а область действия каждого квантора распространяется до конца формулы.

ПНФ – это формула вида 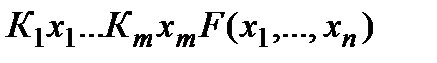, где 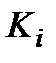– один из кванторов " или $ ( 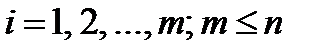), а формула F не содержит кванторов и является приведенной формой.

Для формул логики предикатов справедлива следующая теорема.

Теорема. Для каждой формулы логики предикатов существует равносильная ей ПНФ.

Предваренные нормальные формы формул в логике предикатов используются для выяснения равносильности формул и для решения проблемы классификации формул.

Одной из задач классификации формул является проблема разрешимости, которая состоит в следующем. Необходимо найти алгоритм, при помощи ко­торого для произвольной формулы логики предикатов можно опре­делить, будет она тавтологией или нет. В отличие от алгебры выска­зываний, для формул логики предикатов общего алгоритма не су­ществует. Это было доказано в 1936 году американским математиком А. Чёрчем. Несмотря на отсутствие алгоритма в общем случае, в неко­торых частных случаях такой алгоритм существует. Например, для формул, содержащих только одноместные предикаты.

6. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ (ИП)

Понятие формулы в ИП вводится так же, как оно вводилось в логике предикатов.

Аксиоматическая теория начинается с выбора системы аксиом. Как и в случае высказываний, этот выбор может быть осуществлен по-разному. Одной из таких систем аксиом может служить система, состоящая из трех аксиом рассмотренного выше формализованного исчисления высказываний и двух дополнительных аксиом (схем аксиом):

(P1) ;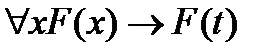

(P2) ,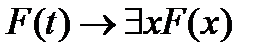

где формула t не содержит свободной переменной x.

К правилу вывода modus pones(MP) добавляются еще два правила вывода:

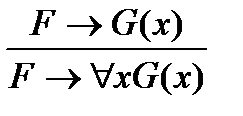	– правило введения квантора общности ("–правило);
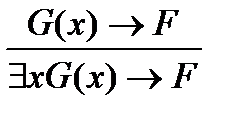	– правило введения квантора существования ( $– правило),

где х не входит свободно в формулу F.

Понятия вывода и теоремы определяются аналогично соответствующим понятиям исчисления высказываний.

Возможны и другие системы аксиом и правил вывода.

Рассмотрим пример вывода в исчислении предикатов.

Пример. Доказать, что

.

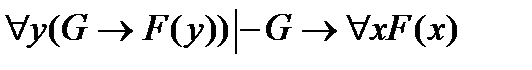Решение.Построим вывод второй формулы из первой:

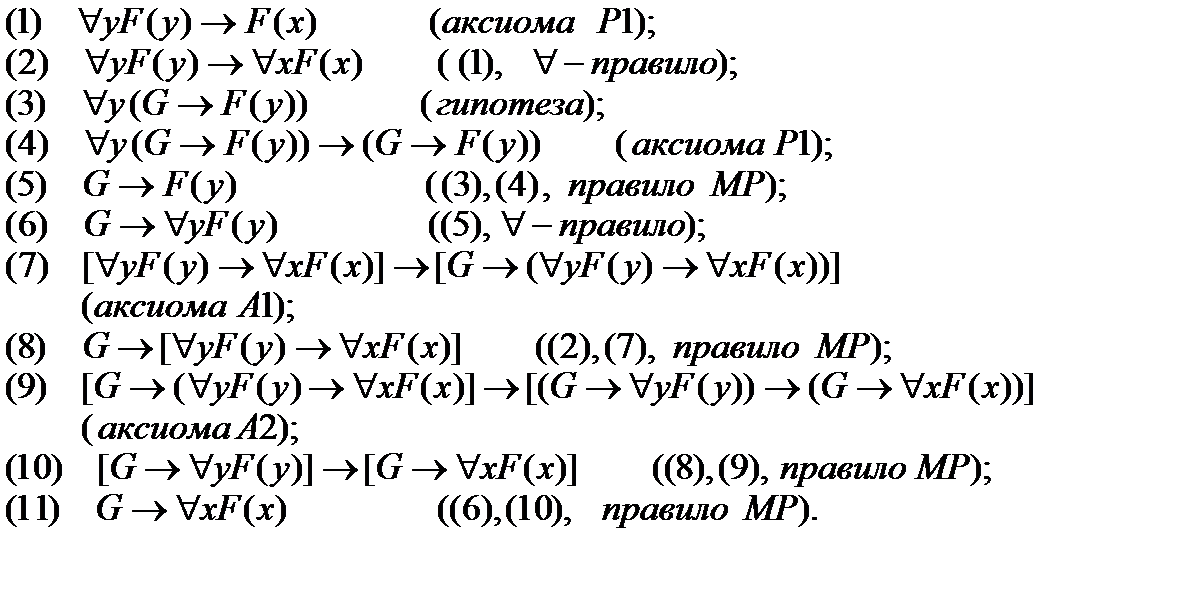
Библиографический список

1.Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник – практикум и решения: Учебное пособие. 3 – е изд., испр. – СПб.:Издательство «Лань», 2008. – 288 с.

2.Дискретная математика: Теория, задачи, приложения / Я.М. Ерусалимский. – 7-е изд. – М.: Вузовская книга, 2005. – 268 с.: ил.

3.Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов: учеб.пособие для студ. высш.учеб.заведений / В.И.Игошин. – 2-е изд.,стер. –М. : Издательский центр «Академия», 2006. – 304 с.

4.Игошин В.И. Математическая логика и теория алгоритмов: Учеб.пособие для студ. высш.учеб.заведений / В.И.Игошин. –М. : Издательский центр «Академия», 2004. – 448 с.

5.Успенский В.А., Верещагин Н.К., Плиско В.Е. Вводный курс математической логики. – 2-е изд. – М.: ФИЗМАТЛИТ, 2002. – 128 с.

6.Математическая логика и теория алгоритмов. Ч. I: Метод. указания / Казан. гос. технол. ун-т; Сост. А.В.Садыков. Казань, 2005. 48 с.

Содержание

1. ЛОГИКА ВЫСКАЗЫВАНИЙ …….………….…….… 3

1.1. Высказывания и операции над ними …………………3

1.2. Формулы алгебры высказываний …………………… 5

1.3. Классификация формул. Равносильные формулы….. 6

1.4. Нормальные формы ……………………………….....11

1.5. Логическое следование ………………………………18

1.6. Правила вывода ………………………………………21

2. ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ И ИХ ПРИЛОЖЕНИЯ …………………………………………….25

2.1. Функции алгебры логики ……………………………25

2.2. Специальные замкнутые классы функций
алгебры логики ……………………………….…...… 30

2.3. Приложение булевых функций к анализу
и синтезу релейно-контактных схем.................……. 33

3. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ ……..….……… 35

4. ПРАВИЛО РЕЗОЛЮЦИЙ…….………………………41

5. ЛОГИКА ПРЕДИКАТОВ ………………..…….……. 43

4.

5.

5.1. Определение предиката ……………………….……. 43

5.2. Логические операции над предикатами …….……... 45

5.3. Теоретико-множественный смысл предикатов…..…48

5.4. Классификация предикатов …………………….….. 50

5.5. Формулы логики предикатов.
Равносильность формул …………………….……… 50

5.6. Классификация формул логики предикатов……… 52

6. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ ……………….…… 55

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ………………….. 57

Учебное издание

Садыков Айдар Вагизович