Анализ выполнения заданий этой темы
По разделу «Основы логики» в экзаменационной работе содержится четыре задания: два с выбором ответа и два с кратким ответом. Одно задание базового, два повышенного и одно – высокого уровня сложности. Экзаменуемые хорошо справились с заданием А3 базового уровня на проверку умения строить таблицы истинности и логические схемы: 79% выполнения в среднем. Результат практически эквивалентен предыдущим годам. Результат выполнения задания А10 повышенного уровня на проверку знания основных понятий и законов математической логики также выше результатов прошлых лет: 74% [2, 90 c.].
Как и в прошлые годы задание В12 повышенного уровня сложности на умение осуществлять поиск информации в Интернете с использованием логических операций дало результат в среднем 51%. Результат выполнения задания В15 высокого уровня сложности с кратким ответом на умение строить и преобразовывать логические выражения составил 69%.
В целом в 2013 году по теме «Основы логики» результаты полностью соответствуют и иногда даже превосходят результаты, прогнозировавшиеся комиссией. Можно сделать окончательный вывод о том, что повышенное внимание, уделенное этому разделу при разборе результатов ЕГЭ предыдущих лет, дало свои плоды: результат усвоения этой темы не выбивается из общего ряда.
Глава 3. Решения задач ЕГЭ по теме «Основы логики»
А3.Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?

1) X Ù Y Ù Z 2) X Ù Y Ù Z3) X Ù Y Ù Z4) X Ú Y Ú Z
Решение:
1) перепишем ответы в других обозначениях: 1) 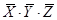 2)
2) 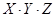 3)
3) 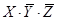 4)
4) 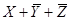
2) в столбце F есть единственная единица для комбинации 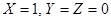 , простейшая функция, истинная (только) для этого случая, имеет вид
, простейшая функция, истинная (только) для этого случая, имеет вид 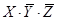 , она есть среди приведенных ответов (ответ 3)
, она есть среди приведенных ответов (ответ 3)
3) таким образом, правильный ответ – 3.
А 10.На числовой прямой даны два отрезка: P =[10?30] и Q=[25,55]. Определите наибольшую возможную длину отрезка A, при котором формула (xÎA)→((xÎP)Ú(xÎQ)) тождественна истинна, то есть принимает значение 1 при любом значении переменной x.
1) 10 2) 20 3) 30 4) 45
Решение:
1) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами
A: x Î А, P: x Î P, Q: x Î Q
2) перейдем к более простым обозначениям
A → (P + Q)
3) раскроем импликацию через операции НЕ и ИЛИ ( 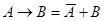 ):
):
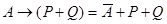
4) для того, чтобы выражение было истинно при всех x, нужно, чтобы 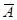 было истинно там, где ложно
было истинно там, где ложно 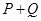 (жёлтая область на рисунке)
(жёлтая область на рисунке)

5) поэтому максимальный отрезок, где A может быть истинно (и, соответственно, 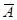 ложно) – это отрезок [10,55], имеющий длину 45
ложно) – это отрезок [10,55], имеющий длину 45
6) Ответ: 4.
В12. В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| Динамо & Рубин | |
| Спартак & Рубин | |
| (Динамо | Спартак) & Рубин |
Сколько страниц (в тысячах) будет найдено по запросу Рубин & Динамо & Спартак?
Решение (вариант 1, круги Эйлера, полная диаграмма):
1) в этой задаче неполные данные, так как они не позволяют определить размеры всех областей; однако их хватает для того, чтобы ответить на поставленный вопрос
2) обозначим области, которые соответствуют каждому запросу
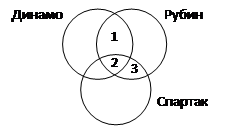
| Запрос | Области | Количество страниц (тыс.) |
| Динамо & Рубин | 1+2 | |
| Спартак & Рубин | 2+3 | |
| (Динамо | Спартак) & Рубин | 1+2+3 | |
| Рубин & Динамо & Спартак | ? |
3) из таблицы следует, что в суммарный результат первых двух запросов область 2 входит дважды (1 + 2 + 2 + 3), поэтому, сравнивая этот результат с третьим запросом (1 + 2 + 3), сразу находим результат четвертого:
N2 = (320 + 280) – 430 = 170
4) таким образом, ответ – 170.
В 15. Сколько различных решений имеет система логических уравнений
(x1®x2)® (x3®x4)=1
(x3®x4)® (x5®x6)=1
Где x1, x2,…,x6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение (метод замены переменных):
1) используем замену переменных (заметим, что каждая из новых переменных независима от других, это важно!):
Y1 = x1 ® x2, Y2 = x3 ® x4, Y3 = x5 ® x6
тогда система запишется в виде
Y1 ® Y2 = 1
Y2 ® Y3 = 1
2) можно объединить эти уравнения в одно
(Y1 ® Y2) Ù (Y2 ® Y3) = 1
для того, чтобы это равенство было выполнено, ни одно из импликаций не должна быть ложной, то есть в битовой цепочке, составленной из значений переменных Y1, Y2, Y3, не должно быть последовательности «10»; вот все возможные варианты:
| Y1 | Y2 | Y3 |
3) теперь вернемся к исходным переменным; импликация x1 ® x2 дает 0 при одном наборе исходных переменных (x1,x2) = (1,0) и 1 при трёх наборах (x1,x2) = {(0,0), (0,1), (1,1)}
4) учитывая, что каждая из новых переменных Y1, Y2, Y3, независима от других; для каждой строки полученной таблицы просто перемножаем количество вариантов комбинация исходных переменных:
| Y1 | Y2 | Y3 | вариантов |
| 1*1*1=1 | |||
| 1*1*3=3 | |||
| 1*3*3=9 | |||
| 3*3*3=27 |
5) складываем все результаты: 1 + 3 + 9 + 27 = 40
6) Ответ: 40.
Заключение
Тема «Логика. Логические основы компьютера» – один из разделов, изучаемых в рамках учебной дисциплины «Информатика и ИКТ» на профильном уровне.
Изучение логики развивает: ясность и четкость мышления; способность предельно уточнять предмет мысли; внимательность, аккуратность, обстоятельность, убедительность в суждениях; умение абстрагироваться от конкретного содержания и сосредоточиться на структуре своей мысли.
Важна роль задач в изучении этого раздела. Ученики должны понимать, что логика в силу своей предельной общности и абстрактности имеет отношение буквально ко всем конкретным отраслям науки и техники.
В работе представлены решения задач по теме «Основы логики», взятые из демо-версий ЕГЭ по информатике разных лет.
Таким образом, в результате проделанной работы были достигнута цель и решены поставленные задачи.
Список литературы
1. Бочкин А. И. Методика преподавания информатики. – Минск: Высшая школа, 2007. – 431 с.
2. ЕГЭ 2013. Информатика. Федеральный банк экзаменационных материалов / Авт.-сост. П. А. Якушкин, С. С. Крылов. — М. : Эксмо, 2013. — 160 с.
3. Информатика : ЕГЭ-2013 : Самые новые задания/авт.-сост. О.В. Ярцева, Е.Н. Цикина. — М.: ACT: Астрель, 2013. — 126 с.
4. Информатика и ИКТ: Учебник. Начальный уровень / Под ред. Н. В. Макаровой. — СПб.: Питер, 2011.
5. Информатика и ИКТ: Учебник. 8-9 класс / Под ред. Н. В. Макаровой. — СПб.: Питер, 2011.
6. Информатика и ИКТ: Практикум. 8-9 класс. / Под ред. Н. В. Макаровой. — СПб.: Питер, 2011.
7. Информатика и ИКТ: Учебник. 10 класс. Базовый уровень / Под ред. Н. В. Макаровой. — СПб.: Питер, 2011.
8. Информатика и ИКТ: Учебник. 11 класс. Базовый уровень / Под ред. Н. В. Макаровой — СПб.: Питер, 2011.
9. Информатика и ИКТ: Методическое пособие для учителей. Т. 1. / Под ред. проф. Н. В. Макаровой. — СПб.: Питер, 2011.
10. Информатика и ИКТ: Методическое пособие для учителей. Т. 2. / Под ред. проф. Н. В. Макаровой. СПб.: Питер, 2011.
11. Информатика и ИКТ: Методическое пособие для учителей. Т. 3. / Под ред. проф. Н. В. Макаровой. СПб.: Питер, 2011.
12. Лапчик М. П. и др. Методика преподавания информатики. – М.: Академия, 2011. – 624 с.
13. Лыскова В. Ю., Ракитина Е. А. Логика в информатике. – М.: ЛБЗ, 2011. – 160 с.
14. Молодцов В.А. Информатика : тесты, задания, лучшие методики / Молодцов В.А., Рыжикова Н.Б. — Ростов н/Д : Феникс, 2008. — 217 с.
15. Подготовка к ЕГЭ по дисциплине «Информатика и ИКТ» / Под ред. Н. В. Макаровой. — СПб.: Питер, 2011.
16. Семакин И. Г., Шеина Т. Ю. Преподавание базового курса информатики в средней школе. Методическое пособие. – М.: БИНОМ. ЛБЗ, 2012.
17. Софронова Н. В. Теория и методика обучения информатике. – М.: Высшая школа, 2009. – 223 с.
