Некоторые арифметические и логические операции
Комплексные данные
В системе MATLAB по умолчанию переменным i и j присвоено значение 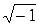 . В этой связи следует предупредить об опасности, связанной с присвоением указанным переменным новых значений (например, при их использовании в качестве параметров цикла, что часто встречается в программах на языке FORTRAN). Чтобы избежать подобной ситуации перед началом работы с комплексными числами следует выполнять команду
. В этой связи следует предупредить об опасности, связанной с присвоением указанным переменным новых значений (например, при их использовании в качестве параметров цикла, что часто встречается в программах на языке FORTRAN). Чтобы избежать подобной ситуации перед началом работы с комплексными числами следует выполнять команду
>> clear i, j
Задание комплексных чисел
>> x=1+i
x=
1.0000 + 1.0000i
>> y=3-4i
y=
3.0000 - 4.0000i
Другой вариант задания комплексных чисел с помощью функции complex
>> x=complex(1,1)
x=
1.0000 + 1.0000i
>> y= complex (3,-4)
y=
3.0000 - 4.0000i
Вычисление произведений комплексных чисел
>> x*y
ans=
7.0000 - 1.0000i
Вычисление 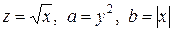
>> z=sqrt(x)
z=
1.0967 + 0.4551i
>> a=y^3
a=
-1.1700e+02 - 4.4000e+01i
>> b=abs(x)
b=
1.4142
Вычисление действительной (p=Re y)и мнимой (q=Im y) частей комплексного числа y с помощью стандартных функций real и imag
>> p=real(y)
p=
>> q=imag(y)
q=
-4
Нахождение числа, комплексно сопряженного числу y
>> conj(y)
ans=
3.0000 + 4.0000i
Такого же результата можно добиться, располагая апостроф вслед за комплексным значением
>> w=3+4i’
w=
3.0000 - 4.0000i
Вычисление cos y
>> cos(y)
ans=
-27.0349+3.8512i
Некоторые приемы работы с матрицами и векторами
Примеры
1. Задание вектор строки (одномерного массива)
>> u1=[1 1 4]
u1=
1 1 4
>> whos u1
Name Size Bytes Class Attributes
u1 1x3 24 double
Для задания вектор - строки используются квадратные скобки, в которых числовые данные отделяются друг от друга пробелами или запятыми.
2. Задание вектор - столбца (одномерного массива)
>> v=[3; 1; -2;]
v=
-2
>> whos v
Name Size Bytes Class Attributes
v 3x1 24 double
Заметим, что в качестве разделителей у вектор – столбца используются точки с запятыми.
3. Транспонирование вектора
>> h=v’
h=
3 1 -2
>> whos v
Name Size Bytes Class Attributes
h 1x3 24 double
4. Задание вектора с помощью числового диапазона
>> r=2: 0.2 : 3
r=
2.0000 2.2000 2.4000 2.6000 2.8000 3.0000
>> whos r
Name Size Bytes Class Attributes
r 1x6 48 double
Таким образом, значения компонент вектора, вычисляемые по закону арифметической прогрессии, формируются по шаблону: начальное значение: шаг: конечное значение.
5. Поэлементное умножение векторов
>> a=[1 2 4];
>> b=[3 2 0];
>> a*b
ans=
3 4 0
6. Создание матрицы (двумерного массива)
>> A=[4 -1 1; 3 2 6; 10 2 25]
A=
4 -1 1
3 2 6
10 2 25
>> whos r
Name Size Bytes Class Attributes
A 3x3 72 double
7. Выделение заданного столбца матрицы (двумерного массива)
>> A(:,3)
ans=
8. . Выделение заданной строки матрицы (двумерного массива)
>> A(2,:)
ans=
3 2 6
Некоторые арифметические и логические операции
Операции над числовыми величинами
| символ | Выполняемое действие |
| + | Покомпонентное (поэлементное) сложение числовых массивов одинаковой размерности; добавление скалярной величины к каждому элементу массива |
| - | Покомпонентное (поэлементное) вычитание числовых массивов одинаковой размерности; вычитание скалярной величины от каждого элемента массива |
| * | Умножение матриц в соответствии с правилами линейной алгебры; умножение всех элементов массива на скаляр |
| .* | Покомпонентное умножение элементов массивов одинаковой размерности |
| / | Деление скаляра на скаляр; покомпонентное деление всех элементов массива на скаляр; A/B=A*B 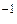 (A, B – квадратные матрицы одного порядка (A, B – квадратные матрицы одного порядка |
| \ | A\B=A 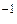 *B (левое матричное деление, А – квадратная матрица) *B (левое матричное деление, А – квадратная матрица) |
| .\ | A. \В - покомпонентное деление элементов массивов одинаковой размерности |
| ^ | Возведение скаляра в любую степень; вычисление целой степени квадратной матрицы |
| .^ | Покомпонентное возведение в степень элементов массива |
| ‘ | Вычисление сопряженной матрицы |
| .’ | Транспонирование матрицы |
Операции сравнения
| == | Проверка на равенство |
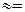 | Проверка на неравенство |
| > | Проверка на «больше» |
| >= | Проверка на «больше или равно» |
| < | Проверка на «меньше» |
| <= | Проверка на «меньше или равно» |
Элементарные математические функции
ВСТРОЕННЫЕ ФУНКЦИИ
| Функция | Обозначение в системе MATLAB |
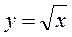 | y=sqrt(x) |
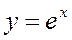 | y=exp(x) вычисляет экспоненциальную функцию от элементов числового массива. Области определения и значений могут быть комплексными. |
| y=ln x | y=log(x) вычисляет натуральный логарифм от элементов числового массива. Области определения и значений могут быть комплексными. |
| y=lg x | y=log10(x) вычисляет десятичный логарифм от элементов числового массива. Области определения и значений могут быть комплексными. |
| y=sin x | y=sin(x) вычисляет синус от элементов числового массива. Области определения и значений могут быть комплексными. Углы измеряются в радианах. |
| y=cos x | y=cos(x) вычисляет косинус от элементов числового массива. Области определения и значений могут быть комплексными. Углы измеряются в радианах. |
| y=tg x | y=tan(x) |
| y=arcsin x | y=asin(x) |
| y=arccos x | y=acos(x) |
| y=arctg x | y=atan(x) |
| y=ctg x | y=cot(x) |
| y=arcctg x | y=acot(x) |
| y=sec x | y=sec (x) |
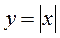 | y=abs(x) |
К лабораторной работе:
Записать на алгоритмическом языке следующие арифметические выражения:
1. 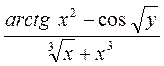
(atan(x^2)-cos(sqrt(y))/(x^(1/3)+x^3)
2. 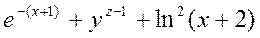
exp(-(x-1))+y^(z-1)+log(x+2)^2
3. 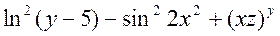
log(y-5)^2-sin(2*x^2)+(x*z)^y
4. 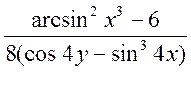
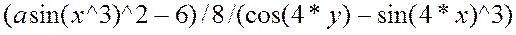
Задание. Написать программу вычисления
1. 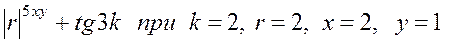
2. 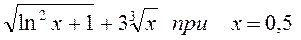
3. 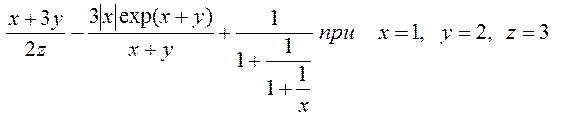
4. 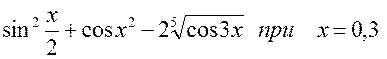
Для выполнения создается М-файл. Ниже приведен текст М-файла.
k=2; r=2; x=2; y=1;
r1=abs(x)^(5*x*y)+tan(3*k)
x=.5;
r2=sqrt(log(x)^2+1)+3*x^(1/3)
x=1;y=2;z=3;
r3=(x+3*y)/(2*z)-3*abs(x)*exp(x+y)/(x+y)+1/(1+1/(1+1/x))
x=0.3;
r4=sin(x/2)^3+cos(x^2)-2*cos(3*x)^(1/5)
Для просмотра результатов работы операторов знак «;» не ставится.
Результаты (в командном окне)
r1=
1.0237e+003
r2=
3.5978
r4=
-18.2522
r4=
-0.8193
