Определение 1. Пусть и произвольные множества. Соответствием называется тройка множеств 7 страница

Откуда на основании 1а, 4а, 5б, 3а, 4а, 1б и 5б имеем

( ) ( ( ) ( (

( ( ( .

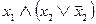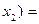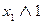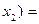
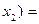
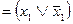
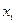
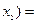
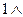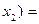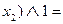
Таким образом, ( ) ( ) ( ) 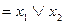. Теперь сравним полученный результат с табл. 5.1.

Пример 5.12. Упростить совершенную ДНФ для импликации.

Решение. Согласно табл. 5.1 импликация может быть определена по формуле ( ) ( ) ( ).

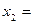Упростим правую часть равенства. Применяя тождества 3б, 1а, 4а, 1б, 5б, 3а, 1а, 4а, 1б и 5б, получим

( ) ( ) ( ( )) (

)) ( ( ) ( (

.

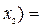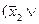
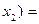
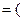
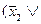
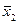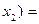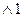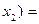
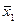
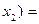
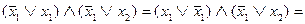
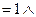
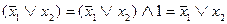Таким образом, искомая формула будет

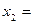
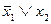. (5.24)

Правая часть равенства (5.24) представляет конъюнкцию неполных дизъюнкций. Такие формулы называются сокращенными ДНФ. В примерах 5.11 и 5.12 был осуществлен переход от совершенных ДНФ к сокращенным. Сокращенные ДНФ можно задавать также матрицами, только матрицы эти будут уже не булевыми (как в случае ДНФ), а троичными. Ее столбцы - это троичные векторы, каждый из которых в общем случае может определять грань гиперкуба. Например, троичные матрицы для сокращенных ДНФ, полученных в примерах 3 и 4, будут такими:

, .

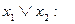
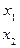
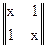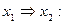
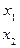
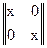Здесь первый столбец первой матрицы определяет грань 1x размерности 1, т.е. ребро с вершинами 10 и 11. Аналогично второй столбец x1={01, 11} и столбцы второй матрицы 0x={00, 01}, x1={01, 11}.

Напомним, что число символов «x» в троичном векторе определяет размерность грани. Например, грань 1xx куба имеет размерность 2 и представляет собой множество {100, 101, 110, 111}, что соответствует четырем столбцам булевой матрицы. Поэтому троичные матрицы по сравнению с булевыми более компактно описывают одну и ту же булеву функцию.

Вопросы для самоконтроля

1. Постройте булеву матрицу для совершенной ДНФ ( ) ( ) ( 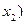) ( . Затем с помощью алгебраических преобразований определите сокращенную ДНФ и постройте для нее троичную матрицу. Сравните результаты.

2. Для функции 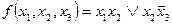найдите совершенную ДНФ.

3. Дайте объяснение тому, что двойная инверсия - пустая операция.

5.2.5. Конъюнктивные нормальные формы

Наряду с совершенными и сокращенными ДНФ в булевой алгебре используются также совершенные и сокращенные конъюнктивные нормальные формы (КНФ), которые также могут задаваться в виде матриц.

Пример. 5.13. Дана функция

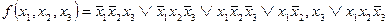. (5.25)

Найти совершенную ДНФ для инверсии данной функции.

Решение. Функция 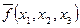имеет область истинности, равную области ложности заданной функции 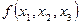. Область истинности этой функции согласно (5.25) представлена следующими пятью вершинами {001, 010, 100, 101, 110}. Тогда ее область ложности будет содержать все остальные вершины куба (рис. 5.9), т.е. множество {000, 011, 111} – ее область ложности и область истинности функции 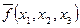. Значит булева матрица функции 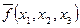имеет вид

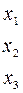
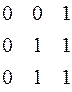, откуда .

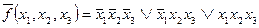Пример 5.14. Используя законы Де Моргана (10а, 10б), выразить функцию из предыдущего примера в виде конъюнкции дизъюнкций.

Решение. Поскольку двойная инверсия - пустое преобразование, то

.

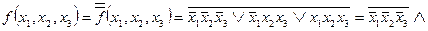
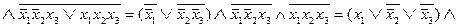
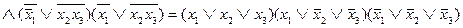Полученная формула для функции (5.25) называется совершенной КНФ. Ее можно строить по области ложности функции по следующему правилу.

Если область ложности состоит из 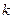вершин, то записывается конъюнкция 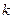одинаковых дизъюнкций из всех переменных (полных элементарных дизъюнкций), от которых зависит функция. Затем ставится знак инверсии над теми переменными, которые соответствуют координатам вершин, равным единице.

Для нашего примера областью ложности было множество {000, 011, 111}. Поэтому

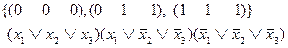
Совершенную КНФ не имеет только одна булева функция – константа «истина», т.к. ее область ложности - пустое множество.

Конъюнкции из неполных дизъюнкций образуют сокращенную ДНФ.

Например, формула 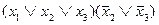будет уже сокращенной ДНФ, т.к. одна из ее дизъюнкций неполная (во второй дизъюнкции отсутствует переменная ).

Сокращенные КНФ нашли применение в алгоритмах исчисления предикатов методом резолюций. На основе данного метода разработан транслятор языка программирования ПРОЛОГ. Этот язык программирования [1] имеет большое сходство с языком логики предикатов, основные языковые формы которого будут рассматриваться в следующей главе.

На множестве функций сравнения можно построить и другие алгебры, например, существует так называемая алгебра Жегалкина с сигнатурой 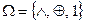, позволяющая выразить любую двухзначную логическую функцию и выполнять преобразования. Здесь мы вплотную подходим к понятию базиса логических функций.

Вопросы для самоконтроля

1. Определите совершенные ДНФ и КНФ функции, область истинности которой пересечение двух граней 1xx0 и x1x0.

2. Какая функция имеет следующую совершенную КНФ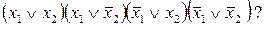

3. Определите совершенные КНФ для эквивалентности и сложения по модулю 2.

5.2.6. Классы булевых функций. Понятие базиса

Существует строгое формальное доказательство того, что любую булеву функцию можно выразить через определенный набор других функций, т.е. представить в некотором базисе.

Определение 23.Система переключательных функций {f₁, f₂, ..,f_k} является полной в классе B и называется базисом в том случае, если любая переключательная функция fÎB может быть представлена посредством функций f₁, f₂, ..,f_k с использованием перенумерации аргументов или подстановки.

Для доказательства этого факта рассмотрим некоторые классы булевых функций, обладающие определенными свойствами.

Самодвойственные функции

В математике существует понятие двойственности. Самодвойственными называются функции, двойственные самим себе. Применительно к булевым функциям.

Определение 24.Самодвойственной называется булева функция, которая на противоположных наборах аргументов принимает противоположные значения, т.е.

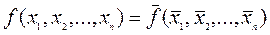. (5.26)

Монотонные функции

Набор аргументов некоторой многоместной булевой функции представляет собой булев вектор. Введем отношение сравнения наборов. Будем считать, что один набор не больше другого, если одноименные значения аргументов одного набора не превосходят соответствующие значения второго набора.

Например, (1,0,0,1)£(1,0,1,1), (1,0,1,0)£(1,0,1,1). В то же время, неверно, что (1,0,0,1) £(1,0,1,0).

Очевидно, что данное отношение образует частичный порядок на множестве наборов аргументов.

Монотонной называется булева функция, если при возрастании наборов аргументов ее значения не убывают.

Здесь, естественно, считается, что 1>0.

Линейные функции

Определение 25.Функция f(x₁,…,x_n) называется линейной, если существуют a₀, a₁,…,a_nÎ{0,1} такие, что

f (x₁,…,x_n)=a₀ 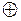a₁x₁ 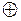… 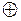a_n x_n, (5.27)

т.е. если функция представима линейным полиномом Жегалкина. Здесь в качестве операции по умолчанию подразумевается логическое умножение, т.е. конъюнкция (например, a₁x₁ тождественно a₁ Ù x₁).

Например, инверсия является линейной функцией ( 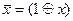), функция конъюнкции не линейна.