Отчет по лабораторной работе № 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

САНКТ-ПЕТЕРБУРГСКИЙ «ГОРНЫЙ» УНИВЕРСИТЕТ

Отчет по лабораторной работе № 1

По дисциплине: Методы математической статистики в маркшейдерском обеспечении

Характеристики случайного распределения результатов измерений горно-геологических показателей

Выполнил: ст. гр. ГГ-12-1 _________ Большаков А. Н.

(подпись) (Ф. И. О.)

Проверил: асс. каф. МД _________ Алексенко А. Г.

(подпись) (Ф. И. О.)

Дата: 22.11.2016

Санкт-Петербург

Цель работы – изучение начальных понятий математической статистики, способа построения вариационного ряда, нахождения числовых характеристик статистических значений показателя.

В качестве примера рассмотрена выборка представленная в таблице 1. В данной таблице указано содержание свинца в полиметаллических рудах (в %), объемом 100 значений.

Таблица 1 – Выборка результатов определения содержания свинца

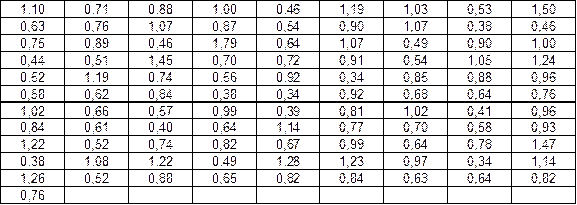
Содержание полезного компонента в рудном теле может принимать любые значения, поэтому данные случайные величины являются непрерывными. Для непрерывной случайно величины составляют интервальные вариационные ряды. Величина интервала подсчитывается по формуле Стерджеса (1):

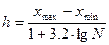(1)

где 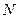– объем выборки; 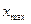– максимальное значение из выборки; 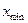– минимальное значение из выборки.

В выборке значения показателей 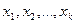называются вариантами, а объем каждого варианта 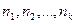– его частотой.

Для сопоставимости вариационных рядов с различными объемами выборок используют значения относительных частот или частостей, вычисляемых по формуле 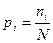(2):

(2)

Для упрощения вычислений при отработке вариационных рядов удобно пользоваться условными значениями вариантов 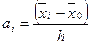(3):

(3)

где 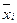– среднее значение показателя в i-м интервале; 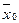– среднее значение интервала с наибольшей частотой.

Положение центра распределения определяют:

– математическим ожиданием;

– модой;

– медианой.

Для оценки рассеивания отдельных значений относительно центра пользуются:

– дисперсией;

– СКО;

–коэффициентом вариации;

– асимметрией;

– эксцессом.

Среднее выборочное значение показателя 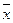рассчитывается по формулам 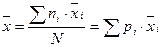(4):

(4)

Мода – значение показателя, которое имеет наибольшую вероятность (частоту). Мода рассчитывается по формуле (5):

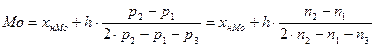(5)

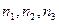где и 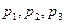– частоты и частости предыдущего, модального и последующего интервалов вариационного ряда соответственно; 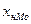– нижняя граница модального интервала.

Медиана – значение показателя в выборке, которое делит ряд распределения по частоте или частости на две равные части. Медиану определяют по формулам 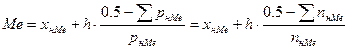(6):

(6)

где 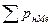, 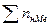– накопленные частости или частоты до начала медианного интервала.

Приближенная оценка симметричности распределения:

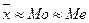– симметричное распределение;

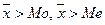– левосторонняя асимметрия;

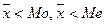– правосторонняя асимметрия.

Выборочная дисперсия 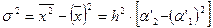(7):

(7)

где 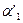, 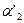– условные моменты первого и второго порядка соответственно.

Условные моменты (8):

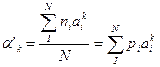(8)

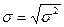СКО (9):

(9)

Коэффициент вариации характеризует относительную величину рассеивания значений показателя 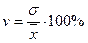(10):

(10)

Асимметрия 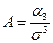(11):

(11)

где 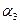– центральный момент третьего порядка: .

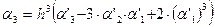Оценка симметричности распределения:

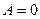–симметричное распределение;

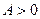– левосторонняя асимметрия;

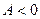– правосторонняя асимметрия.

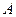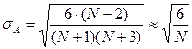СКО величины (12):

(12)

Асимметрию считают не существенной, если .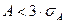

Эксцесс (оценка «крутизны» эмпирической кривой) 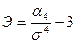(13):

(13)

где 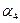– центральный момент четвертого порядка: .

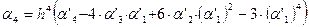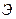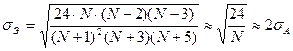СКО величины (14):

(14)

Эксцесс существенный, если .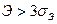

Результаты вычислений представлены ниже.

Величина интервала по формуле (1):

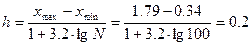
Таблица 2 – Распределение вариационного ряда

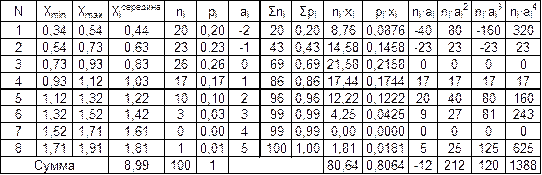
Среднее выборочное значение показателя 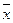по формуле (4):

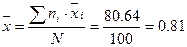
Мода по формуле 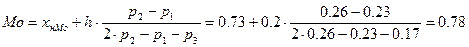(5):

(5)

Медиана по формуле 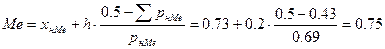(6):

(6)

Приближенная оценка симметричности распределения:

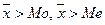– левосторонняя асимметрия.

Выборочная дисперсия 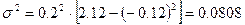(7):

(7)

где 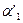, 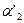– условные моменты первого и второго порядка соответственно.

СКО (9):

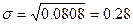(9)

Коэффициент вариации характеризует относительную величину рассеивания значений показателя 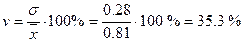(10):

(10)

Асимметрия 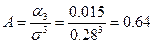(11):

(11)

Оценка симметричности распределения:

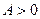– левосторонняя асимметрия.

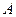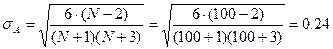СКО величины (12):

(12)

Асимметрия несущественная, так как .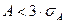

Эксцесс 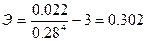(13):

(13)

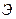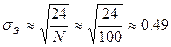СКО величины (14):

(14)

Эксцесс несущественный, так как .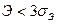

Также была выполнена проверка гипотезы по двум критериям. Для этого была создана таблица, содержащая вероятности попадания в интервал, накопленные вероятности и их разности – таблица 3.

Значение 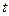рассчитано по формуле:

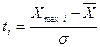(15)

Значения функции плотности распределения были взяты из таблицы, а также вычислены использованием встроенной статистической функции в табличный процессор MS Excel.

Вероятность попадания в интервал 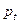получена по формуле:

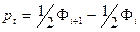(16)

где первое значение .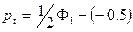

Теоретические частоты получаются путем умножения 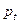на число измерений .

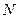Накопленные вероятност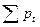и и 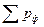получаются последовательным суммированием 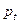и 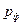. Величина .

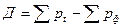Таблица 3 – Вероятности попадания в интервал, накопленные вероятности

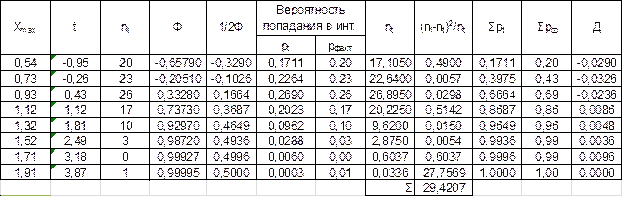
Критерий согласия Пирсона вычисляется по формуле:

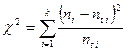(17)

где 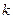– число интервалов.

Гипотеза соответствия распределения наблюденного ряда случайных величин нормальному закону принимается, если соблюдается услови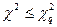е: , где 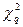– значение, выбираемое по числу степеней свободы 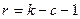( 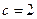при нормальном законе распределения).

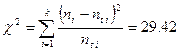, а 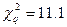, следовательно, можно сделать вывод о несоответствии нормальному закону распределения по критерию согласия Пирсона.

Критерий согласия Колмогорова:

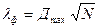(18)

Гипотеза принимается, если соблюдается условие: 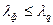. Значения 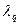зависят от уровня значимости. В нашем случае .

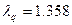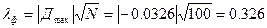, следовательно, можно утверждать о близости фактического распределения величин к нормальному по критерию согласия Колмогорова.

По результатам расчетов были построены эмпирическая и теоретическая кривые распределения показателя.

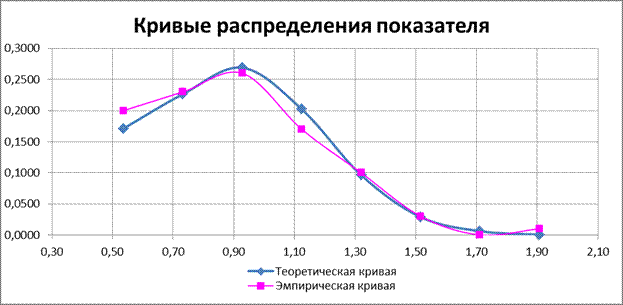
Рисунок 1 – Эмпирическая и теоретическая кривые распределения показателя

Вывод: в данной лабораторной работе были изучены начальные понятия математической статистики, способ построения вариационного ряда, нахождение числовых характеристик статистических значений показателя, а также некоторые критерия отнесения распределения величин к нормальному распределению.