Формулы исчисления высказываний
Кафедра математики, ТиМОМ
Валицкас А.И.
ЗАДАЧНИК ПО
МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
Тобольск – 2010
С О Д Е Р Ж А Н И Е
| ГЛАВА I | АЛГЕБРА ВЫСКАЗЫВАНИЙ . . . | |
| § 1. Понятие высказывания и логические операции с высказываниями . . . . . | ||
| § 2. Формулы исчисления высказываний . . . | ||
| § 3. Истинностные значения формул исчисления высказываний . . . . . . . | ||
| § 4. Равносильные формулы исчисления высказываний | ||
| § 5. СДНФ и СКНФ . . . . . . | ||
| § 6. Булевы функции . . . . . . | ||
| § 7. Логическое следование. Необходимые и достаточные условия . . . . . . . | ||
| ГЛАВА II | АЛГЕБРА ПРЕДИКАТОВ . . . . | |
| § 1. Предикаты, области определения, истинности и ложности . . . . . . . | ||
| § 2. Кванторы. Равносильные предикаты . . . | ||
| § 3. Формулы исчисления предикатов . . . | ||
| § 4. Интерпретации формул исчисления предикатов . | ||
| § 5. Предварённо-приведённая нормальная форма . | ||
| ГЛАВА III | ФОРМАЛЬНЫЕ АКСИОМАТИЧЕСКИЕ ТЕОРИИ | |
| § 1. Формальные теории ИВ и ИП . . . . | ||
| § 2. Формальные теории ИВ и ИП . . . | ||
| ГЛАВА IV | ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ ПО ЛОГИКЕ . | |
| Приложение 1 | Теорема об основных законах логики . . . | |
| Приложение 2 | Теорема об основных равносильностях . . . | |
| Приложение 3 | Теорема об основных правилах логического вывода . | |
| Приложение 4 | Теорема об основных равносильностях с кванторами . | |
| Приложение 5 | Аксиоматика ИВ и ИП |
ГЛАВА I. АЛГЕБРА ВЫСКАЗЫВАНИЙ
Понятие высказывания и логические
Операции с высказываниями
1.Какие из следующих предложений являются высказываниями ? Ответы обоснуйте. Какие значения истинности имеют высказывания ?
а) “Который сейчас час ?”, б) “Сегодня пятница”, в) “Верно ли, что 2 + 1 = 3 ?”, г)“Сегодня, 30 сентября 2012 года, в г. Тобольске пятница”, д)“2´2 = 4”, е) “Если сегодня пятница, то будет лекция по алгебре”, ж) “Сегодня, 29 декабря 2009 года, в 21-00 по московскому времени в г. Тобольске произойдёт лунное затмение”, з) “3 – простое число”, и) “Сегодня, 29 декабря 2009 года, в 21-00 по московскому времени произойдёт солнечное затмение”, к) “В этой комнате холодно”, л) “Поскольку число p простое, оно имеет ровно два различных натуральных делителя: единицу и само число p”, м) “В геометрическом центре самой большой комнаты трёхкомнатной квартиры по адресу г. Тобольск, IV мкр., д. 4, кв. 48, температура воздуха сегодня, 22 июня 1866 г., равна 180 С”, н) “Если все точки данной фигуры равноудалены от заданной точки плоскости, то эта фигура является окружностью”, о) “Натуральное число называется простым, если оно имеет ровно два различных натуральных делителя: единицу и само число”, п) “Окружностью называется геометрическое место точек плоскости, равноудалённых от заданной точки плоскости”, р) “Дом, в котором Вы сейчас зарегистрированы, обогревается с помощью парового отопления”.
2.Какие из следующих предложений являются высказываниями ? Ответы обоснуйте. Какие значения истинности имеют высказывания ?
а) “Если 2´2 = 4, то это утверждение, которое Вы сейчас читаете или слышите, истинно”, в) “Высота треугольника – это прямая, проходящая через его вершину и перпендикулярная противолежащей стороне”, г) “Если предыдущее предложение является определением, то Вы – Папа Римский”, д) “Среди предложений задачи 1 главы I § 1 задачника по математической логике для студентов ТГСПА шесть или семь являются высказываниями”, е) “Среди предложений задачи 2главы I § 1 задачника по математической логике для студентов ТГСПА, решаемой Вами сейчас, четыре или пять являются высказываниями”, ж) “Предложение е) задачи 2 главы I § 1 задачника по математической логике для студентов ТГСПА является высказыванием”, з) “Предложение з) задачи 2главы I § 1 задачника по математической логике для студентов ТГСПА является высказыванием”.
3.Какие из следующих высказываний истинны, а какие ложны ? Ответы обоснуйте.
а) 2 Î { х Î R | 2·х3 – 3·х2 + 1 = 0}, б) – 3 Î { х Î R | 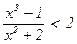 }, в) {1} Î N, г) Æ Î Æ, д) Æ Î {Æ}, е) {Æ} Î {Æ}, ж) Æ = {Æ}, з) 2 = {2}, и) 2 Î {2}, к) e = π,л) 0 < ln 2 < 1, м) sin
}, в) {1} Î N, г) Æ Î Æ, д) Æ Î {Æ}, е) {Æ} Î {Æ}, ж) Æ = {Æ}, з) 2 = {2}, и) 2 Î {2}, к) e = π,л) 0 < ln 2 < 1, м) sin 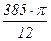 > 0, н) tg
> 0, н) tg 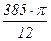 > 0, о) 2 π > 3 e, п)
> 0, о) 2 π > 3 e, п) 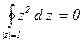 .
.
4.Выясните, какие из данных противоречивы и почему :а)x = 0, (x Ù y) = 1; б)a = 1, (a Ú b) = 1; в)x = 1, (x Ú b) = 0; г)u = 0, (u Ú v) = 0; д) a = 1, (b ® a) = 1; е)b = 1, (b ® a) = 0; ж)В = 1, (x « y) = 1, ( 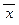 « y) = 1; з)
« y) = 1; з) 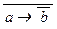 = 0, (a Ú b) = 0, (a Ù b) = 0.
= 0, (a Ú b) = 0, (a Ù b) = 0.
5.Из следующих высказываний с помощью операций конъюнкции, дизъюнкции и импликации сконструируйте истинное и ложное высказывания: а) 2´2 = 5, 3´3 = 9, б) “2´2 = 4 и 3´5 = 16”, “3 – простое число или 8 – составное”, в)“если 2´2 = 4, то 3´3 = 9”, “если 2´2 = 4, то 3´3 = 7”, г) “если 2´2 = 4, то 3´3 = 9”, “если 2´2 = 4, то 5´5 = 25”, д) “неверно, что 2´2 = 4 эквивалентно 3´3 = 8”, “из 3´3 = 12 следует 2´3 = 8”.
6.Существуют ли три таких высказывания a, b, c, для которых одновременно выполнялись следующие условия: а) ( 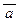 Ù b) = 0, (b ® (aÚ c)) = 0, (
Ù b) = 0, (b ® (aÚ c)) = 0, ( 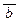 ®
® 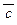 ) = 1; б) (a Ù
) = 1; б) (a Ù 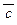 ) = 0, (a Ù b Ù
) = 0, (a Ù b Ù 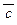 ) = 0, (
) = 0, ( 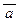 Ù b) = 1; в) (b Ù
Ù b) = 1; в) (b Ù 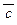 ) = 0, (
) = 0, ( 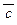 ® a) = 0, (a ® b) = 0; г) (
® a) = 0, (a ® b) = 0; г) ( 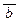 Ù c) = 0, (a Ú
Ù c) = 0, (a Ú 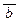 )= 1, (a ® c) = 0; д) (
)= 1, (a ® c) = 0; д) ( 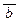 Ù c) = 0, (a Ú
Ù c) = 0, (a Ú 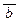 ) = 1, (a® c) = 1; е) (
) = 1, (a® c) = 1; е) ( 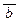 Ù c) = 1, (a Ú
Ù c) = 1, (a Ú 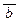 ) = 0, (a ® c) = 0, ж) ((a ® b)® a) = 1, b = 0 ?
) = 0, (a ® c) = 0, ж) ((a ® b)® a) = 1, b = 0 ?
7.Решите системы уравнений:
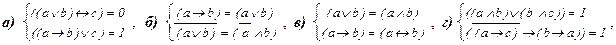
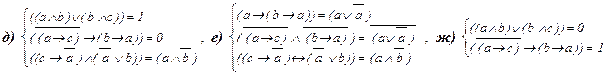 .
.
Формулы исчисления высказываний
1.Какие записи являются формулами ИВ, а какие – нет (обоснуйте ответ) ?
а) (a Ù b) ® 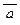 , б) (a ®
, б) (a ® 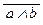 ), в) ((a Ú
), в) ((a Ú 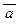 ) Ù (b ® c)), г)
) Ù (b ® c)), г) 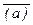 , д) (((aÚ
, д) (((aÚ 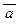 ) Ù (b ® c)), е) (a ®
) Ù (b ® c)), е) (a ® 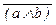 ), ж)
), ж) 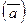 , з) ((a Ù b) ®
, з) ((a Ù b) ® 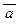 ), и) ((a Ù b) Ú a) ® ((
), и) ((a Ù b) Ú a) ® (( 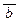 ® c) « (a Ú c))).
® c) « (a Ú c))).
2.Восстановите скобки, превратив в формулы ИВ следующие выражения:
а) a ® b Ú 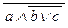 «
« 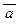 Ù b ® c Ú
Ù b ® c Ú 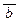 ;б) a Ù (b Ú c) «
;б) a Ù (b Ú c) « 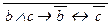 ® b Ú c; в) (a ®
® b Ú c; в) (a ® 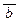 Ù c Ú b «
Ù c Ú b « 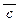 ; г) a ®
; г) a ® 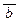 Ù c Ú b) «
Ù c Ú b) « 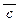 ; д) a ®
; д) a ® 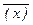 « x Ù
« x Ù 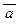 .
.
3.Удалите все лишние скобки в формулах так, чтобы после их восстановления (по правилам восстановления скобок) получились исходные формулы:
a) ((a ® b) ® c);б) (a Ú (b Ù c)); в) 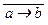 Ú a; г) ((a Ú b) Ù c); д) (a ® (b ® c));
Ú a; г) ((a Ú b) Ù c); д) (a ® (b ® c));
е) ((( 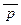 Ù q) « r) Ú (y ® p) Ù q);ж) (((x « y) « ((((x Ù z) Ù x) Ú
Ù q) « r) Ú (y ® p) Ù q);ж) (((x « y) « ((((x Ù z) Ù x) Ú 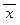 ) ® y)) Ú y);
) ® y)) Ú y);
з) (x ® (( 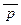 Ú (q Ù r))« (s ® (s ® x)));и) (((x Ú (y Ù z)) « (x Ù y)) ® ((r Ú y) Ù r)).
Ú (q Ù r))« (s ® (s ® x)));и) (((x Ú (y Ù z)) « (x Ù y)) ® ((r Ú y) Ù r)).
4.Расставьте всеми возможными способами скобки (не обязательно по правилам их восстановления) в следующих выражениях, чтобы получились формулы:
а) a Ù b ® c; б) a ® 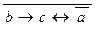 ; в) x ® y Ù
; в) x ® y Ù 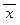 Ú z; г)
Ú z; г) 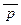 Ú x Ú p ® q;
Ú x Ú p ® q;
д) 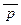 «
« 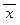 Ú r Ù x; е) x Ú y Ù z Ù x Ú z; ж)
Ú r Ù x; е) x Ú y Ù z Ù x Ú z; ж) 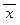 Ú r Ù q Ú r; з) a Ù b ® x Ú
Ú r Ù q Ú r; з) a Ù b ® x Ú 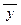 .
.
5.Сколькими способами можно расставить скобки (не обязательно по правилам их восстановления) в выражениях y2 « y3 , y1® y2 Ù y3 , y1 Ù y2 Ù y3 Ù y4 , x1 ® y1 Ù x2 ® y2 , чтобы получилась формула ? Чем отличаются ответы от количеств расстановок скобок в арифметических выражениях y2×y3 , y1×y2×y3 , y1×y2×y3×y4 , x1×y1×x2×y2 соответственно ?
6.Сколькими способами можно расставить скобки в выражении y1 Ù y2 Ù … Ù yn , чтобы получилась формула ? А в выражении x1 ® y1 Ù x2 ® y2 Ù … Ù xn ® yn ?
7.Сколько существует формул ИВ без отрицаний от двух переменных длин 1, 2, 3, 4, 5, 6, 7, 8 ? Изменятся ли ответы, если рассматривать формулы от трёх переменных ?
8.Сколько существует формул ИВ без отрицаний длины n от четырёх пропозициональных переменных для а) n = 1, б) n = 2, в) n = 3, г) n = 4. Тот же вопрос для формул от произвольного числа пропозициональных переменных.
9.Можете ли Вы указать зависимость количества формул ИВ без отрицаний длины n от количеств формул меньших длин ?
10.К формуле ИВ приписали n символов и снова получили формулу ИВ. В каких случаях это возможно ? а) n = 1, б) n = 2, в) n = 3, г) n = 4. А другие значения n могут быть ?
