Условия истинности сложных суждений, состоящих из простых категорических суждений, основываются на допущении двузначности и задаются при помощи таблиц истинности.
3.1. Таблица истинности для конъюнкции:
| p | q | p & q | | И | И | И | | И | Л | Л | | Л | И | Л | | Л | Л | Л | | p, q – пропозициональные переменные, обозначающие простые суждения. То есть p - (S есть P) и q - (S есть P). Буква "И" означает истину, а буква "Л" означает ложь. Каждой строке таблицы соответствует сложное суждение. |
Соединительные (конъюнктивные) суждения истинны тогда, когда истинны все входящие в него простые суждения (члены конъюнкции). Конъюнкция ложна, если ложен хотя бы один из ее членов.
3.2. Таблица истинности для дизъюнкции:
| p | q | p v q | | И | И | И | | И | Л | И | | Л | И | И | | Л | Л | Л | | а) слабая дизъюнкция истинна, когда истинен хотя бы один из членов дизъюнкции, и ложна, когда все ее члены – ложны; |
| p | q | p 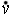 q q | | И | И | Л | | И | Л | И | | Л | И | И | | Л | Л | Л | | б) сильная дизъюнкция истинна только при разных логических значениях членов дизъюнкции и ложна при одинаковых. |
3.3. Таблица истинности для импликации:
| p | q | p → q | | И | И | И | | И | Л | Л | | Л | И | И | | Л | Л | И | | Импликативное суждение истинно во всех случаях, кроме одного, когда антецедент – истинен, а консеквент – ложен. То есть в случае, когда причина возникла, а следствие не наступает, вся импликация является ложной. |
3.4. Таблица истинности для эквиваленции:
| p | q | p 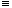 q q | | И | И | И | | И | Л | Л | | Л | И | Л | | Л | Л | И | | Эквивалентные суждения являются равнозначными. Поэтому они истинны при равных значениях членов эквиваленции и ложны – при разных. |
3.5.Таблица истинности для отрицания:
| | «Отрицание» – унарный союз. Если исходное суждение истинно, то его отрицание – ложно, и наоборот. |
Сложное суждение может не только состоять из нескольких простых суждений, но и включать в себя несколько логических связок : (p & q) → p.
Чтобы установить истинность такого суждения, необходимо установить главный логический союз, указывающий на вид суждения, и построить соответствующую таблицу истинности:
| p | q | p & q | (p&q) → p | | И | И | И | И | | И | Л | Л | И | | Л | И | Л | И | | Л | Л | Л | И | | Главный логический союз (в данном случае - импликация) всегда находится в последней колонке таблицы. |
Упражнения:
1. Установите вид следующих сложных суждений и определите их истинность при помощи таблиц истинности:
1.1. Редакция вправе увеличить или уменьшить размер гонорара. (Дизъюкция, истинно)
1.2. Банан - пищевое растение и источник доходов для экспортирующих стран. (Коньюкция, истинно)
1.3. Он сейчас находится в Минске или в Петербурге. (Дизъюкция, истинно)
1.4."Кукушка хвалит петуха за то, что хвалит он кукушку". (Импликация, истинно)
1.5. Если к двум прибавить два, то получится четыре. , (Импликация, истинно)
2. Постройте таблицу истинности для следующего выражения:
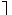 (p→(pvq)).
(p→(pvq)).
| P | Q | PvQ | P→(PvQ) | ך(P→(PvQ)) |
| | | | | |
ТЕМА № 13
"Логика вопросов и ответов".
План:
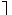 (p→(pvq)).
(p→(pvq)).
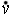 q
q 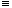 q
q