Надежность элементов системы

Все элементы ЭСК: генераторные агрегаты (ГА), кабели, ГРЩ, РЩ, автоматические выключатели и т.д. могут находится в рабочем (исправном) состоянии или в состоянии отказа. Отказ элементов ЭСК при нормальной эксплуатации является случайным событием. На практике вместо случайных событий оказывается удобным оперировать случайными величинами.

Случайной величиной , называется величина которая в ре­зультате опыта может принять то или иное заранее неизвестное значение. Между случайными событиями и случайными величинами существует связь. Рассмотрим, как устанавли­ваемся такая связь и какие основные случайные величины используются в теории надежности для характеристики эле­ментов.

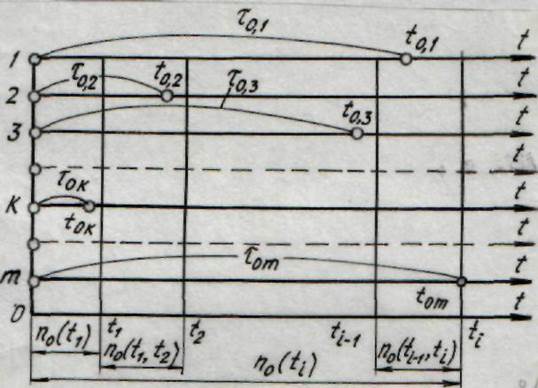
Пусть m одинаковых элементов поставлены на испытания, которые должны выявить их надежность. Например, из партии автоматических выключателей взяты 10 штук и поставлены на испытания по коммутационной износоустойчивости. Испытания проводятся в одинаковых условиях. Каждый автоматический выключатель проработает определенное время и откажет. На рис.8.1. результаты эксперимента показаны графически. Промежутки времени исправной работы от начала испытаний до момента отказа обозначены через, а моменты времени, когда появились отказы, через t _ok. 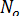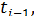Указанную информацию об отказах можно связать либо с непрерывной случайной величиной - временем исправной работы до первого отказа, либо с дискретной случайной ве­личиной [ ] числом отказов элементов за рассматри­ваемый промежуток времени [ 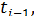] . Условимся случайные величины обозначать большими буквами, а их возможные зна­чения - соответствующими малыми буквами. При подсчете отказов от 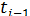= 0 для сокращения записи No (число отказавших элементов) не будем указывать левую границу промежутка времени, т.е. будем писать N₀ .

Наиболее полной характеристикой любой случайной величины являются законы распределения. Законом распределения случайной величины Т называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Функцией распределения случайной величины Т ( или функцией надежности ) называют функцию времени t вида.

Q (t) = P (T –t ),

где P(T< t ) - вероятность отказа элемента до момента t . Эта функция полностью определяет надежности изделия, ра­ботающего до первого отказа.

Наряду с Q(t) часто используется и другая функция:

R(t) = 1 – Q(t) = P (T ≥ t );

которая называется функцией надежности ( работоспособности, безотказности).Она характеризует вероятность того , что отказ не наступит в течении времени t, т.е. вероятность безотказной работы изделия за время ( 0, t ).

Для получения характеристик надежности необходимо знать вероятность отказа какой-либо промежуток времени. Обозначим вероятность отказа Q ( t , t + 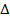t ) или, несколько короче, Q ( t , 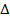t ) Задача, с которой сталкиваются на практике, состоит в оценке неизвестной вероятности отказа, Q ( t , ^t ) по наблюдаемой частоте отказов наблюдаемых элементов:

Q ( t , ^t ) = ,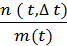

Где 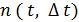- число отказов наблюдаемых элементов в интер­вале времени;

m(t) - общее число изделий, за которыми установлено наблюдение в момент t;

Q ( t , 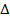t ) - вероятность отказа по частоте.

Получив статистику по вероятности отказа соответст­вующих элементов, можно определить характеристики надежности элементов ЭСК.

8.2. Расчет структурной надежности SCK

После выбора элементов ЭСК основной задачей является построение рациональной структуры первичной и силовой распределительных сетей. Для решения этой задачи выпол­няют расчеты структурной надежности, при помощи которых можно сравнить и оценить варианты схем сетей ЭСК.

ЭСК относится к категории сложных систем, что обуслов­лено не только многочисленностью элементов, но и слож­ностью функциональных и логических связей между элемен­тами и частями системы.

При решении вопросов надежности ЭСК в качестве элемен­тов выступают такие сложные технические устройства как турбогенераторы и дизель-генераторы, различные преобразо­ватели, автоматические переключатели сети, автоматичес­кие пускатели-переключатели, автоматические выключатели и т.д.

Задачасостоит обычно в том, чтобы выявить зависимость надежности структуры системы от важнейших элементов и связей, а затем на основе результатов анализа структуры связей получить максимальную надежность питания потребителей.

Для решения этой задачи необходимо создание простой, но в то же время достаточно логичной математической модели реальной системы. Широкие возможности для построения таких математических моделей дает аппарат алгебры логики, с помощью которого удается достаточно просто описать мно­жество возможных состояний X системы и разбить это мно­жество на два непересекающихся подмножества: работоспо­собных состояний R и неработоспособных состояний (отка­та) Q.

Математическую модель функционирования ЭСК строят обычно на безе простых логических связей. Обычно исходят из положения, что каждый элемент может находиться только в двух несовместных состояниях: работоспособном ( 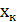= 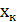), и неработоспособном ( = ).

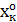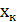Состояние самой системы будет характеризовать m - мерным вектором

= { , ,… ,… } ,

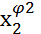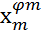Который называется вектором состояний системы. Отказ каж­дого элемента системы является случайным событием, отсюда v вектор 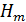является случайной функцией времени 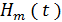, принимающей значения из счетного множества

X = { }.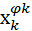

Используя логические связи, существующие между эле­ментами систем можно разделить это множество на под­множества R и Q , удовлетворяющие условиям:

R ∩ Q = ∅ ;R ⋃ Q =X .

Функцию алгебры логики (ФАЛ), связывающую состояние элементов) с состоянием бинарной системы :

y ( ,… ,… )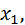

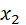будем называть функцией работоспособности системы или условиями работоспособности.

Построенная таким образам математическая модель ЭСК, структура и особенности которой описываются средствами математической логики, количественная оценка надежности производится с помощью теории вероятностей, называется логико-вероятной моделью.

3.2.1. Расчет надежности ЭСК последовательно-параллельной структуры

Все элементы ЭСК (рис.8.2) (генераторы, преобразева.е- ли, щиты, кабели, автгчатически*ьыклЮчатели. потребители и др.) обозначают буквойх_к , гдеk- присвоенный номер эле­мента система. »1апример, ху - генератор GIномер Г носо­вой элегтростанши;rV- генератор номер ^ корм^во.йэлектростанции; Х3 - ГРЩ1 носовойэлектростр.нцгч и т.д. Будем считать, что обозначает.исграЕНое состояние эле­мента системы, а - неисправное состояние элемента (от­каз ). ^: ^^^^ШрЩШ^Ж^ШЯ^^ с

Рис.8.2. Схема без перемычки: а-ъринципиальнал; б - структурная

Для расчета надежности ЭСК необходимо прежде всего ¹ описать условия работоспособности. Зто описание может быть выполнено различными способами:

?) Словесно (см.Рис.8.2): для ЭСК, принципиальная схема которой изображена на рисунке, неоо'ходимо оценить надежность обеспечения питания ответственных потребите­лей, подключенных к распределительному щиту Р1Д1. Постав­ленная задача может 6ыуь выполнена с помощью следующих комбинаций элементов системы:

- исправны, находятся в действии и включены гене­ратор 6ri, ГРЩ1.. автоматические зыключгтелиQFi, QF3, кабель Юш АПС и распределительный гит РЩ1;

- исправны, находятся в действии и включены генера­торG2,ГРЩ2_г автоматические выключатели QFi,(iF^, кабель КГ, АПС я >*спро делительный щит РЩ1. . ^.

б) Графически с помощью структурной схемы (см.рис.8.26)

в) Фоок' лиз^ванно с помощью функций алгебры логик*..

Словесное описание условий работоспособности системы

очень громоздко, плохс обозримо и недостаточно четко. Графическое описание условий работоспособности системы с помощь* структурной схемы является очень наглядным, но, как правило, нелетным и неоднозначном.

Формализованное описание условий работоспособности системы является наиболее четким, полным и однозначным. Описание условий работоспособности или функцию работо­способности получают на основе функции алгебры логики по структурной схеме. Напшмер, для структурной схемы, изображенной на рио.8,2,6, задача обеспечения ддиктри- ческой- энергией РЩ. с ответственными потреби.елями ре­шается следующей функцией '^^отоспособности:

■ (У*)^в*i*i*$*?v'.XtX₄X_sX₇*

> (8.7)

= х₇ (ху Х₃Х₅ V X" Хи х₆ ) ,

где^х)- функция работоспособности ЭСК по зыгто.лнению за­дачи питания о^тветгтвенных потребителей от РЩ1; V - знак логического сложения, дизъюнктен; х^ - генератор № iносовой электростанции; х _л - ГРЩ1; Kj- кабел:>KI;

%2 генератор № 2 кормевой электростанции; х^ Щ ГРЩ2; ' х₆ - кабель К2;

х₇ - АПС, от которого питается РЩ1. Функций работоспособности системы состоит из кратчай­ших путей успеьного санкционирования (КПУФ). КРУ® предс­тавляет собой такую конъюнкцию (логическое умножение/ элементов ЭСК, ни одного из которых нельзя изъять, не нарушив работоспособность системы. Таких кратчайших тей успешного функционирования в нашем примере два:

и *gк₆Они представляют собой последовательное соединенгэ элементов ЭСК и sзляюгеясовогупностью элементов, для которой необходимым и достаточном условием отказа явля­ется отказ хотя бы одного элемента, гходя^его в данную совокупность (коньюнкцию). КПУФ представляет собой опи­сателе одного из возможных самостоятельных путе.. реше­ния задачи. КПУФ в нашем примере включены параллельно на РЩ1 для решения заде, ш обеспечения писанием ответст­венных потребителей, т.е. отказ обоих КПУФ пргводит к срыву яад^чи.

Параллельным соединением элементов называется сово­купность КПУФ, для которой необходимым и достаточным условием отказа системы является отказ всех кратчайших путей успешного функционирования (дизъюнкция ЬЛУФ или логическое сложение); |

В матличном виде формула (8.7) фикции работоспособ­ности записывается:

" | X >XjXf		х* || [	(8.8)
ХцХц X* ' 7		■ "х+х6 1 '

Для количественной оцен. и надежности от функции рабо­тоспособности переходят, к вероятностной функцийs

= i=(?_е , (8.9, где вероятность безУказной работы системыjдая'-ЭС№- вероятность бесперебойного обеспечения питание^ потребителей; •

Дгя нашего примера

- Р { V Щ||xi)|J| « '

Подставив соОтветСФвуяяцие вероятности безотказной ра­боты элементов ЭСК к^ , R; j

P. -P^i-if-R^.Rjjti-f?,!?^,]! • 8.10)

Таким образом,- дйя достаточно ..простой схемы можно рас­считать надежности tii. ганияотв "?тственныхтотребителей. Вероятность безотказной работы каждого .в&зменто ЭСК для расчетов выбирается лз справочников. Эти показатели оп­ределяются по статистическим данным.

8.2.2. Расчет надежности ЭСК с моотиковой структурой

Реальные ЭСК сложнее, чем рассмотренная выше. Они имеют в составе первичных ертей перемычки, которь^то соз­дает определенную избыточность, ^ кратчайших путях успеш- hoijiДофкцррчирования появляются одни и те же эл менты. Функция работоспособности становится повторной, а это ве­дет к погрешностям в течете.

Например, если связать ГРЩ № I и ГРШ № 2.перемычкой П,

т о поставленную задачу и можно олисат? фу нацией раб от о- способности (рис.8.3):

гдеу(<)~ повторная функция рабой способности.

<2

а

Of-oo•

QF6 ¹

(^Нчу-^О

IflHB

Рис.8,Я.4Схема СЭО с перемычкой Л: а- принципиальная; б - структурная

ЧЖ|

Обозначим кратчайший путь успешного функционирования А и запишем (8.9) в матричном виде:

^Х3 ^х5 ^х7^х3 ^х£ ^х4 *7

** ^хв^х7I (8.12)

*_г Х^'Х, X /

Функция работоспособности достаточно громоздкая и яв­ляется повторной при расчете методом, примененным в 2.2.1 для последовательно-параллельной структуры, появилась бы • погрешность. -I , * .

щ
рг
р»
р*

^ - - - ^ . 199'

Достатчноi-росто надежность подобных ЭСК рассчитывают табличг"JMмет о до'-".

Этот метод основан на использовании теоремы слояенил вероятностей совместных событий, в качестве которых здесь вь,скупают элементарные коньюгшии условий работоспособ­ности:

V(?)=VP-\ (8.13)

Щ . Р |ЩIP(PiAP;)+|£ 2 Р I Ш

Необходимо составить специальную таблицу в.10, в кото­рой нужно разместить т строк (по числу элементов в системе).

В названиях строк указываются вероятности безотказной работы элементов/?_х ^, а з названиях столбцов гаписываются' все возможные соединения конъюнкцийР^ . взятых по одной, по две, по три и т.д.

Кроме «Иго, указываются з^т,аки вероятностей этих коньюнк- пий: ^и+" или "~^п, чередующиеся в соответствии с формулой (8.14).

Таблицу заполняют крестиками и черточками, причем крес­тиками там, где отме^тэютзя вероятности событий (элементов), входящих в соответствующую коньюнкгию пути успешного функ- . ционигювания. -

В столбце таблицы вероятности безотказней работы ? .патен­тов, отмеченных крестиками, перемножаются. Затем с учетом зк ка проводится алгебраическое сложение результатов, полу­ченных по столбцам. В итоге поучаем - вепоятность без от­казной работы системы. Таким образом методами, изложенны- - ••и в § 8.2, можно оценить надежность любой структуры ЭСК.

I R- ztk****' ЩМ

20С

Таблица 8.10. Расчетная'i-аблкца для схемы ЭСХ Вероятность раоотоспособ-щШЩ^ ности элементов QT   ОТ* 4* of С? or of a- <3* cc Q? jr Q? 0* •CC of cC" ar <e or <C 0? of CP or . Ш Ш   — Г +   г 2- о 5 1 6 ; 7 II IS   X* X     X X X X v t V > r X X X: X X   / — • — X X _ X X V/ /V X JX X X X X X   X X - X X X X X X X XI X X X X   — X X X X X :x X X X X X X / X   X — — X v A X X - X X X X X X X . 1 1ШШш ' - X X 1 X X 1 w X X X X X X X X   X X X X X X X X X X 1 X Щ Y / N X Ix   — X — X X — x X Л у 1 x ■ Iх X X 'X       я* R« я' {£7 R'   к7U4   R*