Дизъюнктивная нормальная форма (днф)

Формула, представленная в виде дизъюнкции элементарных конъюнкций.

Дизъюнктивное поглощение

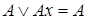, где - некоторая элементарная конъюнкция переменных; - булева переменная.

Дизъюнктивное ядро булевой функции

Такое множество её простых импликант, которое образует покрытие , но после удаления импликанты теряет это свойство, то есть перестает быть полной системой импликант.

Длина полинома Жегалкина

Количество попарно различных элементарных конъюнкций в полиноме Жегалкина.

Единичный элемент (единица)

Элемент 1 из множества .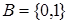

Закон ассоциативности (сочетательный закон)

; .

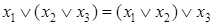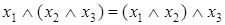Законы де Моргана

; .

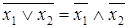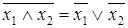Закон дистрибутивности (распределительный закон)

; .

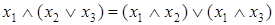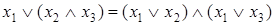Закон идемпотентности

; .

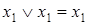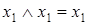Закон инволюции (двойного отрицания)

.

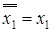Закон исключенного третьего

.

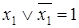Закон коммутативности (переместительный закон)

; .

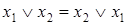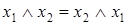Закон поглощения (элиминации)

; .

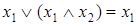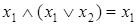Закон противоречия

.

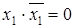Закон тождества (свойство констант)

; ; ; .

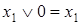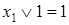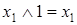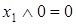Замкнутый класс булевых функций

Класс (множество) называется замкнутым классом, если 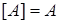(где - некоторое подмножество функций из ).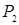

Замыкание множества булевых функций

Множество 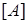, состоящее из функций, представимых в виде формул через функции множества (где - некоторое подмножество функций из ).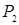

Импликанта

Импликантойнекоторой функции называется функция 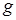, такая, что на всех интерпретациях, на которых 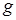равна единице, тоже равна единице.

Имплицента

Импликантойнекоторой функции называется функция 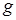, такая, что на всех интерпретациях, на которых 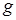равна нулю, тоже равна нулю.

Инверсия

Функция 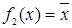, равная 1, когда аргумент принимает значение 0, и равная 0 при аргументе 1.

Индекс (коэффициент) простоты

Коэффициент, характеризующий «сложность» ДНФ (КНФ).

Интерпретация булевой функции

Для булевой функции 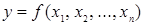конкретное (индивидуальное) значение булевого набора .

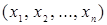Инфисная запись формул

Запись формул, при которой знаки функций стоят между аргументами.

Классы Поста

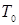− класс функций, сохраняющих 0; 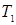− класс функций, сохраняющих 1; − класс самодвойственных функций; − класс монотонных функций; 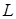− класс линейных функций.

Конституента единицы

Булева функция аргументов, которая принимает значение, равное 1, только на одной интерпретации (наборе).

То же, что и минтерм -го ранга

Конституента нуля

Булева функция аргументов, которая принимает значение, равное 0, только на одной интерпретации (наборе).

То же, что и макстерм -го ранга

Конъюнктивная нормальная форма (КНФ)

Формула, представленная в виде конъюнкции элементарных дизъюнкций.

Конъюнктивное поглощение

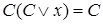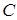, где - некоторая элементарная дизъюнкция переменных; - булева переменная.

Кортеж

Совокупность конкретных значений аргументов булевой функции.

Линейная функция

Булева функция, которая представляется в алгебре Жегалкина каноническим многочленом (полиномом Жегалкина), не содержащем конъюнкций переменных: 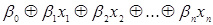, где коэффициенты 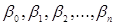, принимающие значение 0 или 1.

Логические переменные

То же, что и булевы переменные.

Логическая функция

То же, что и булева функция.

Макстерм -го ранга

Член конъюнктивной нормальной формы, представляющий собой элементарную конъюнкцию букв.

Макстерм -го ранга

То же, что и конституента нуля.