Отношения между суждениями. Суждения, как и понятия, могут быть сравнимыми (имеют общий субъект и предикат) и несравнимыми (субъект и/или предикат различны)

Суждения, как и понятия, могут быть сравнимыми (имеют общий субъект и предикат) и несравнимыми (субъект и/или предикат различны). Сравнимые суждения по значениям истинности бывают совместимыми (выражают одну и ту же мысль полностью или в некоторой части) и несовместимыми (из истинности одного из них с необходимостью следует ложность другого).

Отношения совместимости: эквивалентность, подчинение и частичная совместимость. Отношения несовместимости: противоположность и противоречие.

Совместимые эквивалентные суждения выражают одну и ту же мысль в различной форме. Например, «Все защитники в суде имеют юридическое образование» и «Все адвокаты – юристы».

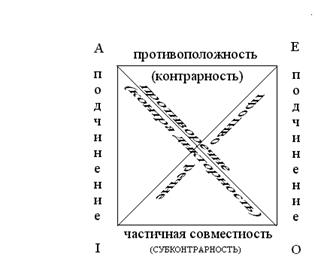Отношения между суждениями по значениям истинности принято схематически изображать в виде так называемого «логического квадрата».

Рассмотрим закономерности, выражающие отношения между суждениями по значениям истинности.

1. Суждения A – I и E – O находятся в отношении подчинения. Суждения A и E – подчиняющие, а I и O – подчинённые.

a. Если подчиняющее суждение истинно, то и подчинённое истинно.

b. Если подчинённое суждение ложно, то и подчиняющее ложно.

2. Суждения I – O находятся в отношении частичной совместимости. Оба они одновременно могут быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно.

3. Суждения A – E находятся в отношении противоположности. Они могут быть одновременно ложными, но не могут быть одновременно истинными. Если одно из них истинно, то другое обязательно ложно.

4. Суждения A – O и E – I находятся в отношении противоречия. Они никогда не имеют одинаковых значений истинности. Если одно из суждений пары истинно, то другое обязательно ложно; если одно из суждений пары ложно, то другое обязательно истинно.

Закономерности, выражающие отношения между суждениями по значениям истинности, имеют большое познавательное значение, так как они помогают правильно делать непосредственные умозаключения (умозаключение из одной посылки).

Логические операции с суждениями

Превращение – это преобразование суждения путём изменения его качества. При этом количество суждения и его субъект не меняются, а понятие предиката меняется на противоположное. Например:

(A) Подлежащее – главный член предложения.

(E) Подлежащее не является второстепенным членом предложения.

Обращение – это преобразование суждения. При котором субъект исходного суждения становится предикатом, а предикат исходного суждения становится субъектом. При этом качество суждения не меняется, а количество может измениться. Например:

(A) Все композиторы – музыканты.

(I) Некоторые музыканты – композиторы.

У М О З А К Л Ю Ч Е Н И Е

Умозаключение как форма мышления

Умозаключение – это форма мышления, посредством которой из одного или нескольких истинных суждений с помощью определённых правил вывода получается новое истинное суждение. Умозаключения бывают дедуктивными, индуктивными и по аналогии.

В дедуктивном умозаключении мысль движется от общего к частному. При соблюдении правил вывода заключение является истинным суждением. В индуктивном умозаключении мысль движется от частного к общему. Вывод является вероятным. При умозаключении по аналогии мысль движется от частного к частному. Вывод при этом носит вероятный характер.

Категорический силлогизм

Категорический силлогизм (простой категорический силлогизм) – это вид дедуктивного умозаключения, в котором из двух истинных простых суждений при соблюдении правил вывода получается новое истинное суждение. Например:

Жидкости (M) упруги (P). – большая посылка

Вода (S) – жидкость (M). – меньшая посылка

Вода (S) упруга (P). – заключение

Понятия «жидкость», «вода» и «упруга» называют терминами силлогизма. S («вода») – субъект заключения, содержится в меньшей посылке и называется меньшим термином. P («упруга») – предикат заключения, содержится в большей посылке и называется меньшим термином. М («жидкость») – содержится в обеих посылках, отсутствует в заключении, служит для связи посылок и называется средним термином.

Силлогизм можно изобразить в круговых схемах Эйлера. Для этого необходимо изобразить посылки, а затем осуществить их совмещение. Так, схемой приведённого выше силлогизма будет следующая:

P

M S

Фигурами силлогизма называются формы силлогизма в зависимости от положения среднего термина. Всего может быть четыре фигуры силлогизма:

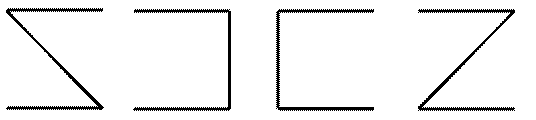
1-я фигура 2-я фигура 3-я фигура 4-я фигура

Модусами фигур силлогизма называют разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в него посылок и заключения. Всего различных модусов существует 256, из них только 19 правильных, по которым можно получить достоверное заключение. По каждой фигуре правильные модусы представлены в таблице (см. справочный материал в конце пособия).

В наших рассуждениях мы часто пользуемся категорическим силлогизмом. Для того чтобы получать правильные выводы, необходимо соблюдать общие правила силлогизма (см. справочный материал в конце пособия). Также практически часто необходимо бывает оценить достоверность полученного в рассуждениях умозаключения. Категорический силлогизм можно проверить разными способами.