Понятие алгоритма и связанных с ним категорий.

Под алгоритмом понимается некоторое конечное предписание, с помощью которого можно найти решение за конечное число шагов задачи из некоторого класса задач..

Алгоритм работает над данными, преобразуя входные данные в выходные. В процессе преобразования могут образовываться промежуточные данные. Входные, выходные и промежуточные данные характеризуются определенной лексикой, т.е. кодируются символами определенного алфавита. Для всякой задачи длина слова входных данных (количество символов в коде данных) называется размерностью задачи над алфавитом входных данных.

Работа алгоритма характеризуется дискретностью, т.е. разбивается на ряд операций. В зависимости от однозначности или неоднозначности перехода между операциями алгоритмы подразделяются на детерминированные и недетерминированные.

Работа алгоритма отличается результативностью. Если алгоритм применим к некоторому слову входных данных, то через конечное число проведенных операций алгоритм построит слово выходных данных результата и останавливается. В противном случае алгоритм не останавливается.

Работа алгоритма производится на некотором устройстве реализации, содержащем процессор для выполнения операций, внешнюю и внутреннюю память для хранения поиска и изменения данных.

Машина Тьюринга

Одним из формальных методов представления алгоритмов является машина Тьюринга (МТ), которая включает следующие компоненты:

1. Устройство управления, имеющее одно из состояний множества

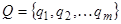..Множество состояний всегда содержит состояние

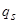, с которого МТ начинает работать, а также состояние 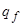, с наступлением которого работа МТ заканчивается;

1. Бесконечную ленту, разбитую на ячейки, в каждой из которых содержится один из символов адфавита 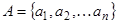.Любой алфавит МТ всегда содержит пустой символ _ - "пробел";
2. Считывающую/записывающую головку, которая в зависимости от текущего состояния устройства управления и от текущего символа на ленте под головкой может передвинуться на одну ячейку вдоль ленты направо (R)., налево (L) или остаться на месте (Е) , а также может записатьв соответствии с заданием в ячейку под собой любой символ из алфавита А .

Задание МТ образует совокупность продукций (команд) 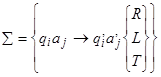, означающих, что, если устройство управления МТ находится в состоянии 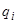, головка "обозревает" на ленте символ 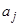, то устройство управления переходит в состояние 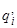, головка МТ записывает в ячейку символ 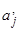(возможно тот же, что и был ранее) и передвигается либо влево на один символ, либо вправо на один символ, либо остается на месте (рис. 4).

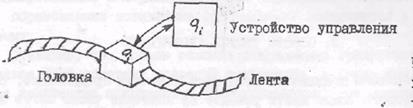
Рис: 4. Машина Тьюринга

Конфигурацией или полным состоянием МТ называется ,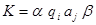

где 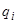- состояние устройства управления; 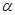- слово над алфавитом слева от головки; 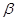- слово справа от головки .первый символ которого 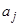-"обозревается" головкой. Выполнение продукции задания приводит к переходу от конфигурации 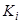к конфигурации .

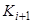Считают, что начальная и заключительная конфигурации МТ таковы, что считывающая/записывающая головка расположена слева от слова исходных данных данных или результата, над первым символом.

Машина Тьюринга правильно реализует некоторую функцию 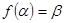(или предикат), если от начальной конфигурации 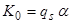за конечное число шагов машина переходит к заключительной конфигурации 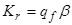, причем если значение 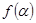- неопределено, то МТ никогда не останавливается.

Любые две МТ считаются одинаковыми, если они реализуют одну и ту же функцию.

Пример 9. Построить копирующую машину MT_С, выполняющую копирование произвольного унарного числа. Для представления чисел на ленте МТ часто используется унарная система. В унарном счислении натуральное число кодируется последовательностью символов «1» количество которых равно величине числа, например число 3 представляется в единичном коде как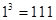

Для распознавания позиции конца слова будем считать, что в конце исходных данных стоит специальный символ .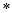

1. Система продукций копирующей MT_С

1.1. 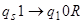- запоминание копируемого символа;

1.2. 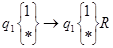-перенос копируемого символа вправо;

1.3. 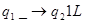-копирование;

1.4. 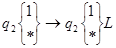- возврат к последней скопированной позиции на ленте

1.5. 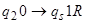- восстановление скопированного символа и продолжение копирования;

1.6. 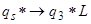- завершение процесса копирования;

1.7. 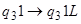- вывод головки в исходное положение;

1.8. 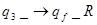- остановка.

Замечание. Продукции 1.2 и 1.4 представляют групповую запись, означающую сходное функционирование МТ при разных данных.

2. Алфавит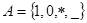

3. Состояния устройства управления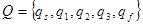

4. Проверочная последовательность конфигураций для контрольного примера исходных данных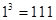

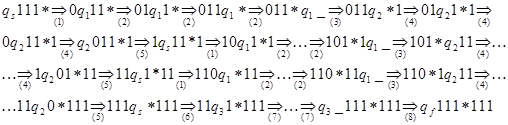
Текущее состояние устройства управления и "обозреваемый" символ называются условиями применения продукции. В отличие от команд алгоритмических языков продукции МТ применяются не в порядке очередности, а при выполнении условий, обозначенных в левой части продукции. Для детерминированной МТ каждая продукция в задании МТ имеет оригинальные условия применения. В недетерминированной МТ одним и тем же. условиям приневения соответствует более одного варианта перехода к следующей конфигура­ции. При выполнении таких продукций недетерминированная МТ создает овои копии по числу вариантов перехода. Все копии сообщаются между собой и также обладают возможностью создавать свои копии при появлении недтерминированной продукции. Недетерминированная МТ завершают свою работу, если хотя бы одна копий переходит в заключительное состояние.

Тезис Тьюринга

Тезис Тьюринга: «всякий алгоритм может быть реализован в виде МТ» - определяет критерий, позволяющий отделить алгоритмически разрешимую проблему от проблем, не относящихся к таковым.

Понятие алгоритмически разрешимых проблем конкретизируют следующие две операции, определенные над множеством МТ.

Композиция МТ

Если МТ₁ и МТ₂ реализуют соответственно функции f1(X) и f2(У) - причем область значений f1 совпадает с областью определения f2, то может быть построена композиция MT=MT₂°MT₁, реализующая функцию. f2(f1(X)). Композиция МТ представляет собой последовательное подключение машин МТ₁ и МТ₂ (последовательный вычислительный процесс), при котором результат первой машины поступает на обработку второй (см. рис.5а).

Для построения МТ композиции ее начальное состояние полагают равным начальному состоянию МТ₁, конечное состояние МТ₁ полагают равным начальному состоянию МТ₂, а конечное состояние композиции полагают равным конечному состоянию MT₂.

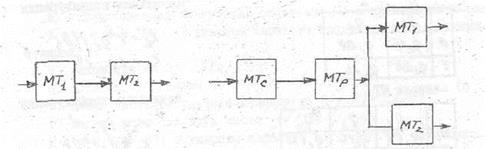
а) б)

Рис. 5. Операции над МТ: а - композиция б - разветвление

Разветвление МТ

Если МТ₁ и МТ₂ реализуют соответственно функции f1(X) и f2(Х) с одинаковыми областями определения, существует МТ_Р, реализующая некоторый предикат Р(х), то может быть построена MT -разветвления , реализующая функцию

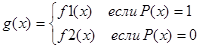
МТ – разветвления представляет параллельное подключение МТ₁ и МТ₂ (разветвление вычислительного процесса ), при котором результат формируется первой машиной, если значение предиката истинно, а иначе - формируется второй. МТ - разветвления начинает свою работу с копирования исходных данных, по одному из экземпляров которых машина предиката вырабатывает признак, указывающий на то, какая из функциональных машин формирует результат.

На­чальное состояние МТ- разветвления полагают равным начальному состоянию МТ композиции, состоящей из последовательного подключения копирующей MT_С, и МТ_Р , реализующей предикат Р . Вводятся две новые продукции:

услови­ям конечного состояния MT_С°МТ_Р и символу 1 (истинности предиката Р), сопоставля­ется начальное состояние MT1,

условиям конечного состояния MT_С°МТ_Р и символу 0 (ложности предиката Р) сопоставляется начальное состояние МТ2.

Конечные состояния МТ₁ и МТ₂ отождествляются с конечным состоянием
МТ - разветвления (рис. 5)

Т.к. интуитивно ясно, что любой алгоритм может быть запрограммирован с помощью последовательных действий и условных разветвлений, то введенные операции позволяют рассматривать МТ как модель алгоритма, анализируя на ней его свойства.