Построение преломляющей границы по данным КМПВ

При расчленении горизонтально-слоистых сред методами сейсморазведки широкое применение нашел КМПВ – корреляционный метод преломленных волн. Это модификация метода преломленных волн, основанная на регистрации и прослеживании (корреляции) первых и последующих вступлений преломленных волн. При инженерно-геологических и гидрогеологических исследованиях метод преломленных волн широко используется для картирования подошвы рыхлых отложений и определения уровня грунтовых вод, для выявления зон трещиноватости и других приповерхностных неоднородностей, а в случае возможности регистрации обменных волн, и для определения механических свойств пород (коэффициента Пуассона и модуля Юнга).

Как известно годограф преломленной волны описывается уравнением:

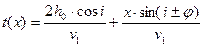; (1)

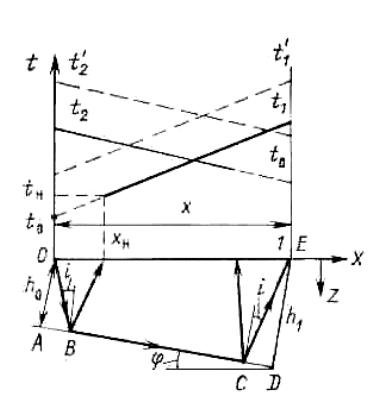где знак «плюс» берут при падении границы в сторону приемника, а знак «минус» - в сторону источника; h₀ - эхоглубина под пунктом возбуждения; φ – угол падения границы; i – критический угол определяемый из соотношения sin i=v₁/v₂; v₁ и v₂ – скорости в верхнем слое и нижнем полупространстве. Таким образом, годограф преломленной волны для наклонной плоской границы в прямоугольных координатах (х, t) - это полупрямая, выходящая из точки с координатами (x_н, t_н), под углом θ к оси ОХ ( рис.1.).

Рис. 1. Схема решения прямой кинематической задачи метода

преломленных волн.

t₁ - прямой годограф;

t₂ - встречный годограф;

t₁’, t₂’ - нагоняющие годографы

Угол θ определяется из соотношения

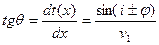
Величину 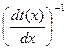называют кажущейся скоростью: v^*=v₁·sin(i±φ)

С учетом того, что sin i=v₁/v₂, получаем

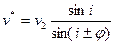(2)

Как видно из выражения (2), кажущаяся скорость может быть больше или меньше скорости в нижней среде. Значения x_н и t_н легко определить из условия ВС=0 (рис.1):

x·cos φ = 2h₀·tg i - x·tg i ·sin φ = ВС = 0. Решая это уравнение, находим

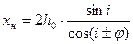
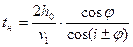(3)

При продолжении годографа преломленной волны до пересечения его с осью t на этой оси отсекается отрезок: t₀= (2h₀/v₁)·cos i.

В начальной точке годографа преломленной волны лучи отраженной под критическим углом волны и первый луч головной волны совпадают между собой. Соотношение между годографами отраженной и преломленной волн для одной и той же границы приведено на рис.2.

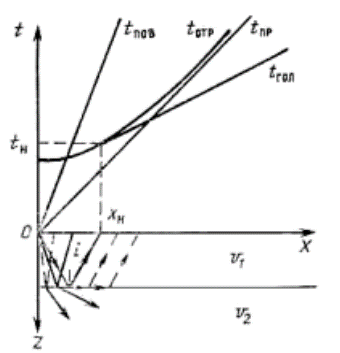
Рис. 2. Соотношение между годографами прямой, отраженной и головной волн.

t_пр - годограф прямой волны;

t_пов - годограф поверхностной волны;

t_гол - годограф головной волны;

t_отр -годограф отраженной волны.

Замечательной особенностью метода преломленных волн является возможность при залегании слоистой толщи на полупространстве или однородном слое большой мощности преломленную от подошвы этой толщи волну наблюдать на таком расстоянии от источника, при котором она приходит к поверхности раньше всех других волн (метод первых вступлений или головных волн). Это свойство преломленных волн широко используют при решении инженерно-геологических и гидрогеологических задач.

При интерпретации метода преломленных волн, как видно из выражения (1), должны быть определены следующие параметры среды: v₁, v₂, φ и h. При наличии только одного годографа преломленной волны сделать это невозможно, требуется дополнительная информация. Однако при наличии встречных годографов и введении некоторых ограничений на модель среды – задача успешно решается.

Одним из простых способов решения обратной задачи в МПВ является способ разностного годографа так же называемый способом t₀. Этот способ имеет два ограничения: 1) предполагается, что в пределах изучаемого участка преломляющая граница является плоской (тем не менее этот способ применим и для слабо криволинейных границ); 2) скорость в покрывающей среде постоянна, т.е. не меняется в пределах изучаемого участка и должна быть определена из других данных (ее можно определить по скважинным данным или по годографу прямой волны).

Фактически в данном способе строится (рис.3) (или рассчитывается) разностный годограф t_p(x) и линия t₀ по формулам:

t_p(x)=t₁(x)+T-t₂(x);

t₀(x)=t₁(x)-T+t₂(x); (4)

затем разностный годограф апроксимируется прямой линией и по ней определяется граничная скорость

v_г=2Δx/Δt; (5)

По известным значениям t₀(x) и v₁ рассчитываются значения эхо-глубин h. Зная эхо-глубины с использованием принципа Гюйгенса строят преломляющую границу, как огибающую окружностей, проведенных из точек наблюдения c радиусами r=t_0iv₁. В случае если угол падения границы не превышает 5-10°, эхо-глубины незначительно отличаются от истинных глубин и границу можно строить откладывая их от поверхности наблюдения.

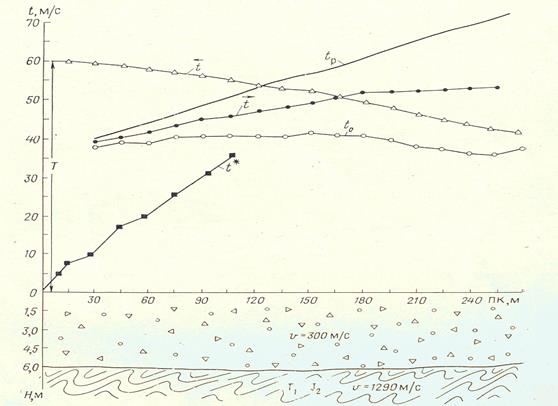
Рис. 3 Сейсмогеологический разрез по данным МПВ.

Порядок выполнения работы

1. Построить годографы первых вступлений
2. Выделить участки на которых регистрируются прямая и преломленные волны
3. Построить разностный годограф преломленной волны
4. Построить линию t₀ для этой волны
5. Определить скорость в верхнем слое по годографу прямой волны у пунктов возбуждения
6. Вычислить глубину залегания преломляющей границы
7. Построить сейсмогеологический разрез, на котором глубины залегания откладываются от линии рельефа
8. Определить граничные скорости
9. В варианте IV найти место смены песчаных отложений на гравийно-галечные в подстилающем слое.

Вариант 1		Вариант 2
пк,м	Рельеф	t1	t2		пк,м	Рельеф	t1	t2
						221,5
	126,5
	126,5
	126,5					223,5
	126,5
						224,5
	124,5
						228,5
	127,5
	127,5
						230,5
	127,5					230,5
	127,5
Вариант 3		Вариант 4
пк,м	Рельеф	t1	t2		пк,м	Рельеф	t1	t2
						210,5
						211,5
						212,5
						214,5
	218,5
						214,5
	216,5