Порядок выполнения лабораторной работы. 1. По последней цифре номера зачетной книжки выбрать задание, случайным образом взять любые десять значений из массива измерений.
1. По последней цифре номера зачетной книжки выбрать задание, случайным образом взять любые десять значений из массива измерений.
2. Выявляем из ряда измерений измерения, резко отличающихся от других (промахов), что позволяет устранить систематическую погрешность, обусловленную влиянием этого ошибочного результата, необъяснимого закономерным случайным рассеиванием результатов. Чтобы обосновать предположение о наличии результата, резко отличающегося от остальных в ряду и подлежащего исключению, все результаты располагаем в порядке возрастания значений 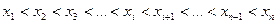 Такой ряд называют вариационным.
Такой ряд называют вариационным.
Для выявления грубой ошибки в измерениях рассчитываем отношения 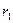 и
и 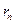 :
:
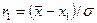 ;
; 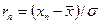 , (3.1)
, (3.1)
где 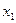 и
и 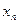 - крайние члены вариационного ряда;
- крайние члены вариационного ряда; 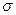 - среднеквадратическое отклонения, рассчитанная по формуле (1.2).
- среднеквадратическое отклонения, рассчитанная по формуле (1.2).
Допустимые числовые значения 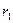 и
и 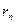 , соответствующие различным доверительным вероятностям, приведены в табл. 3.1 Соответствующие им члены ряда исключаются из него, если для этого члена вычисленное значение
, соответствующие различным доверительным вероятностям, приведены в табл. 3.1 Соответствующие им члены ряда исключаются из него, если для этого члена вычисленное значение 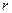 превышает приведенное в таблице. Затем вычисляем средние для остальных членов ряда и производим аналогичный анализ.
превышает приведенное в таблице. Затем вычисляем средние для остальных членов ряда и производим аналогичный анализ.
Число степеней свободы определяется следующим образом:
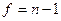 . (3.2)
. (3.2)
Таблица 3.1
Значения 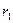 (или
(или 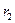 ) для различных доверительных вероятностях
) для различных доверительных вероятностях 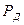
| Число степеней свободы f | 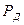 , % , % | Число степеней свободы f | 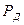 , % , % | ||||||
| 97,5 | 97,5 | ||||||||
| 1,406 | 1,412 | 1,414 | 1,414 | 2,326 | 2,493 | 2,638 | 2,8 | ||
| 1,645 | 1,689 | 1,71 | 1,723 | 2,354 | 2,523 | 2,67 | 2,837 | ||
| 1,791 | 1,869 | 1,917 | 1,955 | 2,38 | 2,551 | 2,701 | 2,871 | ||
| 1,894 | 1,996 | 2,067 | 2,13 | 2,404 | 2,577 | 2,728 | 2,903 | ||
| 1,974 | 2,093 | 2,182 | 2,265 | 2,426 | 2,6 | 2,754 | 2,932 | ||
| 2,041 | 2,172 | 2,273 | 2,374 | 2,447 | 2,623 | 2,778 | 2,959 | ||
| 2,097 | 2,237 | 2,349 | 2,464 | 2,467 | 2,644 | 2,823 | 3,008 | ||
| 2,146 | 2,294 | 2,414 | 2,54 | 2,486 | 2,664 | 2,823 | 3,03 | ||
| 2,19 | 2,343 | 2,47 | 2,606 | 2,504 | 2,683 | 2,843 | 3,03 | ||
| 2,229 | 2,387 | 2,519 | 2,663 | 2,52 | 2,701 | 2,862 | 3,051 | ||
| 2,264 | 2,426 | 2,562 | 2,714 | 2,537 | 2,717 | 2,88 | 3,071 | ||
| 2,297 | 2,461 | 2,602 | 2,759 |
Отчет о лабораторной работе должен содержать:
1. Цель и название лабораторной работы.
2. Результаты измерений разложенные в вариационный ряд.
3. Вывод о количестве грубых погрешностей в результатах измерений.
Контрольные вопросы к лабораторной работе №6
1. Какие способы устранения систематических погрешностей из ряда наблюдений вам известны?
2. В чем сущность выявления грубой погрешности измерения?
Лабораторная работа №7.
Определение истинного значения измеряемой величины
Цель работы
Определить истинное значение измеряемой величины и установить наличие грубых погрешностей результатов измерений.
Теоретические предпосылки
Известно, что при многократных измерениях погрешность измерения от случайных ошибок уменьшается в 4nраз, где n- число измерений. Это связано с их осреднением и получением возможности определения предельной погрешности среднего арифметического значения.
В случае многократных повторных измерений одной и той же величины одним и тем же методом измерения и при отсутствии систематических погрешностей за предельную погрешность метода измерения Δ lim, определяющую доверительный интервал, по закону нормального распределения случайных величин, принимаем значение:
, 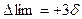 (3.3)
(3.3)
что соответствует доверительной вероятности 0,9973.
Погрешность измерения больше Δlim считают грубой погрешностью и результат измерения с такой погрешностью отбрасывают. Истинное значение измеряемой величины Х(ист) определяет как среднее арифметическое значение ряда измерений:
|
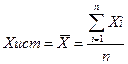
 |
Предельную погрешность среднего арифметического значения S вычисляют по формуле:
гдеσ- средняя квадратическая погрешность.
Результат измерений представляют в виде:
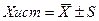
.(3.7)
