Примеры бинарных отношений. 3 страница
Определение. Если  , то множество
, то множество  называется дополнением (абсолютным дополнением, отрицанием)множества
называется дополнением (абсолютным дополнением, отрицанием)множества  .
.
Дополнение множества  , обозначаемое
, обозначаемое  (читается «не
(читается «не  »), – это множество элементов универсума, которые не принадлежат
»), – это множество элементов универсума, которые не принадлежат  , следовательно,
, следовательно,  . Дополнение
. Дополнение  определяется отрицанием свойства
определяется отрицанием свойства  , с помощью которого определяется
, с помощью которого определяется  .
.
Пример:
Если 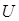 – множество положительных целых чисел, а
– множество положительных целых чисел, а  – множество всех положительных четных чисел, то
– множество всех положительных четных чисел, то  – множество всех положительных нечетных чисел.
– множество всех положительных нечетных чисел.
Определение. Дизъюнктивная сумма (симметрическая разность) – это множество, состоящее из всех элементов  , не принадлежащих
, не принадлежащих  , и всех элементов
, и всех элементов  , не принадлежащих
, не принадлежащих  , и не содержащее никаких других элементов, т.е.
, и не содержащее никаких других элементов, т.е.  .
.
Симметрическая разность, обозначаемая как  , либо
, либо  , либо
, либо  , получается объединением элементов множеств за исключением тех, которые встречаются дважды.
, получается объединением элементов множеств за исключением тех, которые встречаются дважды.
Пример:  ;
; 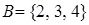 ;
;  .
.
Еще одной часто используемой операцией над множествами является декартово произведение. Обозначение и суть данной операции будут рассмотрены в разделе, связанном с описанием отношений.
Введенные операции называются теоретико-множественными операциями.
Все данные операции на множествах можно проиллюстрировать с помощью диаграмм Эйлера-Венна (рис. 1.5), в которых круги представляют соответствующие множества, участвующие в операциях (например, множество  ), а заштрихованная часть плоскости является результатом выполнения операций (например,
), а заштрихованная часть плоскости является результатом выполнения операций (например, 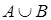 ,
,  ,
, 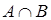 ,
,  ,
, 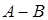 ).
).


а)  б)
б) 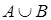


в) 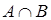 г)
г) 


д) 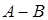 е)
е) 
Рисунок 1.5 Применение диаграмм Эйлера-Венна для иллюстрации операций на множествах
2.3 Общее определение алгебры
Алгебра в широком понимании может быть определена как наука (учение) о системах объектов той или иной природы, в которых установлены алгебраические операции. Для современной алгебры характерно то, что в центре внимания оказываются свойства операций, а не объектов, над которыми производятся эти операции. Алгебра классифицирует системы с заданными на них алгебраическими операциями по их свойствам и изучает различные задачи, естественно возникающие в этих системах.
Введем формализованное понятие алгебры.
Определение. Множество  вместе с заданной на нем совокупностью операций
вместе с заданной на нем совокупностью операций  , т.е. система
, т.е. система  , называется алгеброй. Множество
, называется алгеброй. Множество  – это основное, или несущее, множество (или просто носитель) алгебры.
– это основное, или несущее, множество (или просто носитель) алгебры.  называется сигнатуройи представляет собой множество операций с элементами множества
называется сигнатуройи представляет собой множество операций с элементами множества  . Функция типа:
. Функция типа:  называется
называется  -арной операцией. Вектор арностей операций алгебры называется её типом.
-арной операцией. Вектор арностей операций алгебры называется её типом.
Определение. Операция, заданная на некотором множестве, называется бинарной, если она действует на два элемента этого множества и её результатом является элемент этого же множества.
Определение. Операция, заданная на некотором множестве, называется унарной, если она действует на один элемент множества и её результатом является элемент этого же множества.
Нульарныеоперации – это фиксированные элементы множества  , называются также выделенными элементами, иногда нулями.
, называются также выделенными элементами, иногда нулями.
Определение. Множество  называется замкнутым относительно
называется замкнутым относительно  -арной операции
-арной операции 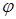 на
на  , если
, если  , т.е. если значения
, т.е. если значения  на аргументах из
на аргументах из  принадлежат
принадлежат  . Если
. Если  замкнуто относительно всех операций
замкнуто относительно всех операций  алгебры
алгебры  , то система
, то система  называется подалгеброй
называется подалгеброй 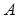 (при этом
(при этом  рассматриваются как операции на
рассматриваются как операции на  ).
).
Примеры алгебр:
1. Алгебра  называется полем действительных чисел. Несущее множество
называется полем действительных чисел. Несущее множество 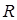 – множество действительных чисел. Операции + и
– множество действительных чисел. Операции + и  – бинарные операции, поэтому тип этой алгебры
– бинарные операции, поэтому тип этой алгебры  . Подалгеброй этой алгебры является, например, поле рациональных чисел.
. Подалгеброй этой алгебры является, например, поле рациональных чисел.
2. Пусть задано множество 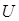 . Множество всех его подмножеств является булеаном
. Множество всех его подмножеств является булеаном 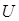 и обозначается
и обозначается  . Алгебра
. Алгебра  называется булевой алгеброй множеств над
называется булевой алгеброй множеств над 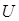 , её тип
, её тип  . Элементами несущего множества этой алгебры являются множества (подмножества
. Элементами несущего множества этой алгебры являются множества (подмножества 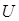 ). Для любого
). Для любого 
 является подалгеброй
является подалгеброй 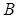 . Например, если
. Например, если  , то основное множество алгебры
, то основное множество алгебры  содержит 16 элементов; алгебра
содержит 16 элементов; алгебра  – подалгебра
– подалгебра  ; её основное множество содержит четыре элемента. Операции
; её основное множество содержит четыре элемента. Операции  являются бинарными, а операция отрицания
являются бинарными, а операция отрицания  является унарной.
является унарной.
2.4 Понятие алгебры множеств. Аксиомы алгебры множеств
Алгебра множеств представляет собой теоретико-множественный аналог обычной алгебры действительных чисел и основана на свойствах операций над множествами.
Определение. Алгебра множеств – непустая совокупность подмножеств некоторого множества  , замкнутая относительно теоретико-множественных операций (объединения, пересечения, разности, дополнения).
, замкнутая относительно теоретико-множественных операций (объединения, пересечения, разности, дополнения).
Для того чтобы некоторый класс подмножеств множества  был алгеброй множеств, достаточно (и необходимо), чтобы он был замкнут относительно образования объединений и дополнений.
был алгеброй множеств, достаточно (и необходимо), чтобы он был замкнут относительно образования объединений и дополнений.
Операции над множествами, как и операции над числами, обладают некоторыми свойствами. Эти свойства выражаются совокупностью формул и тождеств, справедливых независимо от конкретного содержания входящих в них множеств. Данные тождества основаны на следующих аксиомах (законах) алгебры множеств, где  рассматриваются как произвольные подмножества универсального множества
рассматриваются как произвольные подмножества универсального множества 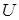 :
:
1. Коммутативные законы
 ,
,
 .
.
2. Ассоциативные законы
 ,
,
 .
.
3. Дистрибутивные законы
 ,
,
 .
.
4. Свойства пустого и универсального множеств
 ,
,  ,
,
 ,
,  .
.
 ,
,  .
.
5. Законы идемпотентности (самопоглощения)
 ,
,
 .
.
6. Закон инволюции
 .
.
7. Закон противоречия
 .
.
8. Закон исключенного третьего
 .
.
9. Законы элиминации (поглощения)
 .
.
 .
.
10.Законы де Моргана
 ,
,
 .
.
Свойствами дополнения, разности и равенства также являются:
11. Если  .
.
12.  .
.
13.  .
.
В справедливости перечисленных выше свойств можно убедиться различными способами:
- нарисовать диаграммы Эйлера-Венна для левой и правой частей равенства и убедиться, что они совпадают;
- провести формальные рассуждения для каждого равенства.
2.5 Принцип двойственности
Практически все рассмотренные тождества (законы алгебры множеств) представлены парами двойственных (дуальных) соотношений, одно из которых получается заменой в другом следующих символов: 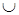 на
на 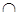 и
и 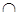 на
на 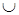 , а также
, а также  на
на 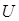 и
и 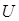 на
на  .
.
Определение. Соответствующие пары символов 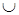 ,
, 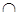 и
и  ,
, 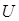 называются двойственными (дуальными) символами.
называются двойственными (дуальными) символами.
При замене в любом законе входящих в него символов дуальными получим новое предложение, которое также является законом. Данное утверждение представляет собой принцип двойственности или дуальности. Законы 11 и 12 не изменяются при замене символов дуальными, поэтому их называют самодвойственными.
Расширяя принцип дуальности на выражения, в которые входит символ включения, необходимо при переходе к дуальному выражению все знаки 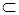 заменить на
заменить на  и обратно.
и обратно.
2.6 Тождественные преобразования формул алгебры множеств
Пользуясь основными тождествами (законами) можно упрощать или преобразовывать к удобному виду различные сложные выражения, содержащие множества, аналогично тому, как проводится упрощение выражений в элементарной алгебре. Для выполнения подобных преобразований применяется следующая приоритетность операций относительно друг друга:  ,
, 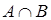 ,
, 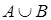 ,
, 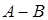 .
.
Такие преобразования осуществляются последовательным применением соответствующих свойств операций над множествами.
Пример. Соотношение  доказывается следующими преобразованиями с использованием рассмотренных законов
доказывается следующими преобразованиями с использованием рассмотренных законов
 .
.
Пример.Упростить выражение  .
.
Для упрощения используем законы алгебры множеств.

=  .
.
Важно отметить, что любое тождество алгебры множеств выводимо из первых четырех свойств, которые в свою очередь доказываются только в терминах отношения принадлежности. Это можно рассматривать как иллюстрацию аксиоматического подхода к алгебре множеств.
2.7 Контрольные вопросы и задания
1. Какие операции над множествами позволяют строить новые множества, используя уже существующие?
2. Какова приоритетность выполнения операций над множествами.
3. Какие способы графической иллюстрации операций над множествами Вы знаете?
4. Поясните обобщенное понятие алгебры. Приведите примеры алгебр.
5. Что такое алгебра множеств?
6. Какая операция над множествами называется бинарной?
7. Какая операция над множествами называется унарной?
8. Назовите основные аксиомы алгебры множеств.
9. Какими свойствами обладает пустое множество 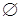 и универсальное множество
и универсальное множество 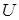 ?
?
10. Опишите принцип двойственности в алгебре множеств, приведите примеры двойственных символов.
11. Поясните способы преобразования формул алгебры множеств.
Лекция 3 Отношения и их свойства. Отношения и операции над ними.
3.1 Декартово произведение множеств
Для формального определения понятия отношения используем понятие декартова (прямого) произведения множеств.
Определение. Декартовым (прямым) произведением множеств  и
и  называется множество, которое обозначается
называется множество, которое обозначается  и состоит из всех тех и только тех упорядоченных пар
и состоит из всех тех и только тех упорядоченных пар 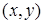 , первая компонента (координата) которых принадлежит множеству
, первая компонента (координата) которых принадлежит множеству  , а вторая компонента (координата) принадлежит множеству
, а вторая компонента (координата) принадлежит множеству  , т.е.
, т.е.  .
.
Пример.
Пусть  ,
,  . Тогда
. Тогда  .
.
Порядок следования пар может быть произвольным, но размещение элементов в каждой паре определяется порядком следования перемножаемых множеств. Следовательно, декартово произведение изменяется при смене порядка сомножителей, и  , если
, если  .
.
Пример.Пусть  ,
,  .
.
 .
.
 .
.
Следовательно,  .
.
Операция декартова произведения легко расширяется и на большее число множеств.
Определение.
Декартовым произведением множеств  называется множество всех возможных упорядоченных наборов
называется множество всех возможных упорядоченных наборов 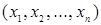 из
из  элементов (кортежей), в которых первый элемент (первая координата) принадлежит множеству
элементов (кортежей), в которых первый элемент (первая координата) принадлежит множеству 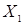 , второй (вторая координата) - множеству
, второй (вторая координата) - множеству 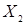 ,
,  -й (
-й (  -ая координата) - множеству
-ая координата) - множеству 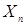 , т.е.
, т.е.  .
.
Пример.
Пусть  ,
,  ,
,  .
.
Тогда 

Если 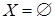 или
или  , то
, то  , так как не существует упорядоченных пар с отсутствующей первой или второй координатой. Аналогично
, так как не существует упорядоченных пар с отсутствующей первой или второй координатой. Аналогично  тогда и только тогда, когда хотя бы одно из множеств
тогда и только тогда, когда хотя бы одно из множеств  является пустым множеством.
является пустым множеством.
Отдельным случаем операции декартова произведения является понятие степени множества.
Определение.
Декартово произведение 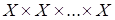 , в котором одно и то же множество
, в котором одно и то же множество  умножается
умножается  раз само на себя, называется декартовой степенью множества и обозначается
раз само на себя, называется декартовой степенью множества и обозначается  . При этом
. При этом  . Множество
. Множество  называется декартовым квадратом множества
называется декартовым квадратом множества  , множество
, множество  - декартовым кубом множества
- декартовым кубом множества  .
.
Пример.Пусть  , тогда
, тогда  ,
,  ,
,  .
.
Пример.
Пусть  - множество действительных чисел, тогда множество
- множество действительных чисел, тогда множество  - множество точек на плоскости.
- множество точек на плоскости.
Определим мощность декартова произведения, используя теорему 3.1.
Теорема 3.1.
Пусть  - конечные множества и
- конечные множества и  ,
,  , …,
, …,  . Тогда мощность декартова произведения
. Тогда мощность декартова произведения  равна произведению мощностей
равна произведению мощностей  .
.
