Предварённо-приведённая нормальная форма

1.Найдите приведённую форму (ПФ) для следующих формул ИП:

а) ($ x (P(x) ® 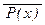)); б) (a « (" y )); в) (R(x) ® ($ y (R(x) Ú Q(x, y))));

г) (P(x) ® ($ y (R(x) Ú Q(x, y)))); д) (R(x, y) « (" x P(x))); е) (Q(x) ® (Q(y) ® Q(x)));

ж) ; з) ; и) ( ® b);

к) (" x (($ y P(x, y)) ® )); л) ® );

м) ($ x ((" y Q(x,y)) ® ($ x (" y P(x,y))));н) (U(p) Ú ($ x (V(x) ® U(x)))).

2.Какие из формул находятся в приведённой предварённой нормальной форме (ППНФ) ?

а) (($ x P(x)) Ù 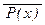)); б) (" x ($ y (P(y) Ú R(x))); в) (" x (($ y P(y)) Ú Q(x)));

г) ( ® b); д) a Ú T(x, y, z); е) (a Ù (" y ));ж) (S(x) Ú U(x, y));

з) ($ y (S(x) Ú U(x, y))); и) (" x ($ y (U(y) ® Q(x))); к) (" x ($ y (Q(y) Ú T(x))));

3.Приведите формулы к ППНФ:

а) (S(x) Ú U(x, y)); б) (($ x R(x)) Ù 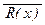)); г) ( ® E(y)); д) P(x, y);

е) (a « (" y ));ж) ($ x ((" y Q(x,y)) ® ($ x (" y P(x,y)))); з) ;

з) (Q(x) ® (Q(y) ® a)); и) ; к) (" x (($ y P(y)) Ú Q(y)));

л) ((P(y) Ú (" y P(y))) ® ( Ù P(y))); м) (R(x, y) « ) ® R(x, x).

ГЛАВА III. ФОРМАЛЬНЫЕ АКСИОМАТИЧЕСКИЕ ТЕОРИИ

Формальные теории ИВ и ИП

1.Докажите, что все аксиомы формального ИВ тождественно истинны.

2.Докажите, что тождественно истинны все аксиомы формального ИП.

3.Докажите следующие теоремы исчисления высказываний:

а) А Ù B ® B Ù A; б) B ® (A ® B Ù A); в) A Ú ® Ú A; г) ;

д) (A Ù B ® C) ® (A ® (B ® C));е) (A ® B) ® ((C ® A) ® (C ® B)).

4.Докажите следующие теоремы исчисления предикатов:

(" z Q(z, t)) ® ($ t Q(t, p)), ($ x P(x, y)) ® ($ y P(y, x)), (" x P(x, y)) ® ($ y P(y, x)),

($ z Q(z)) ® ($ t Q(t)), R(x) ® ($ z R(z)), ((" x P(x, y)) Ù R(y)) ® (" t (P(t, y) Ù R(y))).

5.Докажите следующие теоремы исчисления предикатов:

(" x P(x, y)) « (" z P(z, y)), ($ x P(x, y)) « ($ z P(z, y)),

(" x (" y P(x, y, z))) « (" y Î A (" x Î A P(x, y, z))),

($ x ($ y Î A P(x, y))) « ($ y Î A ($ x P(x, y))),

« ($ x (x, y)), ($ x P(x, y)) « ,

« (" x (x, y)), (" x P(x, y)) « ,

(" x P(x, y)) Ù (" x Q(x, y)) « (" x (P(x, y) Ù Q(x, y))),

($ x P(x, y)) Ú ($ x Q(x, y)) « ($ x (P(x, y) Ú Q(x, y))),

((" x Р(х, y)) Ú R(y)) « (" x (P(x, y) Ú R(y))),

(($ x Р(х, y)) Ú R(y)) « ($ x (P(x, y) Ú R(y))),

((" x Р(х, y)) Ù R(y)) « (" x (Р(x, y) Ù R(y))),

(($ x Р(х, y)) Ù R(y)) « ($ x (Р(x, y) Ù R(y))),

(" х (R(y) ® Р(х, y)) « (R(y) ® (" x Р(х, y))),

($ х (R(y) ® Р(х, y))) « (R(y) ® ($ x Р(х, y))).

(R(y) не зависит от x)

6.Рассмотрим следующую теорию T:

алфавит: {x, Ú, (, )};

формулы: x – формула и, если A, B – формулы, то (A Ú B) – формула, других нет;

аксиомы: x;

правило вывода: ;

Докажите, что

· формула доказуема в теории Т тогда и только тогда, когда она является дизъюнкцией нескольких экземпляров переменной x с любой расстановкой скобок;

· теория T непротиворечива;

· теория T разрешима.

Полна ли теория T в широком смысле ? А в узком ?

7.Расширим теорию T до теории S:

алфавит: {x, 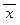, Ù , Ú , (, )};

формулы: x и 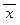– формулы и, если A, B – формулы, то , (A Ù B), (A Ú B) – формулы, других формул нет;

аксиомы: x;

правило вывода: ;

Докажите, что

· формула доказуема в теории S тогда и только тогда, когда она является дизъюнкцией нескольких экземпляров переменной x с любой расстановкой скобок;

· теория S непротиворечива;

· теория S разрешима.

Полна ли теория S в широком смысле ? А в узком ?

8.Приведите пример полной теории (в узком, но не широком смысле; широком, но не узком смысле; в обоих смыслах).

9.Приведите пример противоречивой теории. Она разрешима ? Полна ли она ?