Единицы измерения количества информации на синтаксическом уровне
ИНФОРМАЦИЯ И ИНФОРМАТИКА. АЛГЕБРА ЛОГИКИ. СИСТЕМЫ
СЧИСЛЕНИЯ
(ОСНОВНЫЕ ПОНЯТИЯ)
ПОНЯТИЕ ИНФОРМАЦИИ
Слово «Информация» происходит от латинского слова informatio – сведение, разъяснение, ознакомление. Строгого научного определения информации в настоящее время не существует, принято оперировать понятием об информации, которое рассматривается как базовое понятие и его невозможно определить через другие, более простые понятия. Так же, как, например, понятия точки, луча в геометрии. Содержание базовых понятий выясняется на примерах или путем сопоставления с другими понятиями.
Имеется несколько сотен определений понятия информации. Среди них, например, такие
информация есть отражение различных сторон реального мира,
информация- это продукт взаимодействия данных и адекватных им методов,
информация – есть снятая неопределенность, результат выбора из возможных альтернатив,
информация – это длина алгоритма, позволяющего преобразовать один объект в другой, т.е. мера сложности объекта и т.д.
Федеральный закон «Об информации, информатизации и защите информации» определяет информацию как «сведения о лицах, предметах, фактах, событиях, явлениях и процессах независимо от формы их представления».
Сопоставление всех этих определений понятия информации позволяет сделать заключение об их противоречивости и зачастую специализированной направленности. В настоящее время формируется понимание того, что информатика является комплексным научным направлением, имеющим междисциплинарный характер. В каждой дисциплине понятие информации включено в свою систему понятий в соответствии с предметом изучения, при этом фиксируются каждый раз лишь некоторые, наиболее важные в конкретном контексте, аспекты информации.
Будем описывать информацию, используя категорию «свойство». Данная философская категория выражает такую сторону предмета, которая обусловливает его общность или различие с другими предметами и обнаруживается в его отношении к ним.
Свойства информации.
1. Атрибутивные свойства – это свойства, без которых информация не существует. К ним относятся:
1.1. Непрерывность. Информация имеет свойство сливаться с уже накопленной ранее, тем самым, способствуя ее дальнейшему накоплению.
1.2. Дискретность. Содержащиеся в информации сведения, знания дискретны, т.е. характеризуют отдельные фактические данные и свойства изучаемых объектов, которые распространяются в виде различных сообщений, состоящих из букв, цифр, знаков, цвета, линий.
1.3. Неотрывность от физического носителя.
1.4. Языковая природа информации.
Рассматривая последние два свойства надо учитывать, что жесткой связи информации с конкретным носителем или с конкретным языком нет.
2. Прагматические свойства – характеризуют степень полезности информации для потребителя. К ним относятся:
2.1. Новизна
2.2. Полезность
2.3. Ценность
2.4. Объективность и субъективность (относительность понятия объективности).
2.5. Полнота
2.6. Достоверность
2.7. Адекватность
2.8. Доступность
2.9. Актуальность
3. Динамические свойства – характеризуют изменение информации во времени. К ним относятся:
3.1. Рост информации
3.2. Старение информации
В структуре предметной области информатики можно выделить следующие разделы:
- Теоретическая информатика (теория алгоритмов и автоматов, теория информации, математическая логика, теория формальных языков и грамматик, теория кодирования и др.).
- Технические и программные средства информатизации
- Информационные системы и технологии
Мы будем знакомиться с информатикой в тех аспектах, которые позволяют рассматриватьее как техническую науку, занимающуюся способами создания, хранения, воспроизведения, обработки и передачи данных средствами вычислительной техники, принципами функционирования этих средств и методами управления ими.
ДАННЫЕ
Данные – это зарегистрированные сигналы.
Существуют различные физические методы регистрации данных (изменение магнитных, оптических характеристик поверхностей, состояния электронной системы, химического состава и т.д.). В зависимости от используемого метода регистрации применяются различные типы носителей (бумага, CD-ROM, магнитные диск и лента, триггеры).
Операции с данными:
- сбор данных;
- формализация данных;
- фильтрация данных;
- сортировка данных;
- архивация данных;
- защита данных;
- транспортировка данных;
- преобразование данных.
Последняя операция – важнейшая. Эта операция связанна с переводом данных из одной формы в другую. Преобразование данных необходимо, во – первых, для того, чтобы компьютер или человек мог хранить и обрабатывать данные в удобной для них форме. Во-вторых, многократное преобразование данных необходимо при их транспортировке. В ходе преобразования данных из одной формы представления к другой проводится операция кодирования. Кодирование применяется в различных областях (система записи математических объектов, азбука Морзе, система Брайля для слепых, морская сигнализация флажками и т.д.).
Следует отметить, что в каждой области человеческой деятельности существует множество других, часто весьма специфических операций с данными, которые выполняются в ходе решения различных задач социальной, экономической, научной, промышленной, культурной направленностей.
Данные и информация, грубо говоря, связаны следующим образом: информация – это полезное содержание данных, данные – это форма представления информация. Более полная характеристика указанной связи обеспечивается выделением трех аспектов информации: прагматического, семантического и синтаксического. Прагматический аспект отражает соответствие информации цели, для которой ее предполагает использовать потребитель информации. Семантический аспект отражает степень соответствия объекта и его образа, содержащегося в информации (данных), т.е. речь идет о смысловом содержании информации. Синтаксический аспект затрагивает форму представления информации, но не ее смысловое содержание. Можно сказать, что данные представляют собой информацию в синтаксическом аспекте.
АЛГЕБРА ЛОГИКИ
Высказывание - повествовательное предложение, относительно которого определенно и объективно можно сказать истинно оно или ложно (ЛОЖЬ или ИСТИНА, 0 или 1, TRUE или FALSE). Алгебра логики – раздел математики, изучающий процессы умозаключений и законы, которые позволяют из истинности одних высказываний делать заключения об истинности или ложности других высказываний, независимо от их конкретного содержания. Алгебра логики (булева алгебра) была создана в 1854 г. Дж. Булем и в настоящее время находит широкое применение при разработке алгоритмов и для структурно-функционального описания, анализа и синтеза современных электронных схем.
Базовыми операциями алгебры логики служат операции логического умножения – конъюнкции (обозначается точкой или знаком 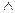 ), логического сложения – дизъюнкции (обозначается знакам + или
), логического сложения – дизъюнкции (обозначается знакам + или 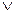 ), логического отрицания – инверсии (обозначается надчеркиванием или знаком
), логического отрицания – инверсии (обозначается надчеркиванием или знаком 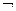 ). При составлении формул применяются скобки, чтобы изменять порядок выполнения операций. Наивысшим приоритетом обладает операция инверсии, затем идет конъюнкция и потом уже дизъюнкция.
). При составлении формул применяются скобки, чтобы изменять порядок выполнения операций. Наивысшим приоритетом обладает операция инверсии, затем идет конъюнкция и потом уже дизъюнкция.
Таблицы истинности для указанных операций:
| А | 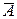 |
| А | В | А 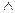 В В |
| А | В | А 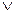 В В |
Представляют интерес еще две логические операции: эквиваленции (обозначается знаком 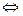 ) и импликации (обозначается знаком
) и импликации (обозначается знаком 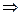 ).
).
| А | В | А 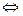 В В |
| А | В | А 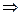 В В |
Приведем основные логические законы (тождественно истинные высказывания), которые позволяют упрощать формулы, заменяя их подформулы эквивалентными выражениями:
1. 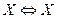 - закон тождества
- закон тождества
2. 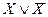 - закон исключенного третьего
- закон исключенного третьего
3. 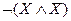 - закон противоречия
- закон противоречия
4. 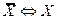 - закон двойного отрицания
- закон двойного отрицания
5. 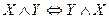 - закон коммутативности конъюнкции
- закон коммутативности конъюнкции
6. 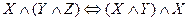 - закон ассоциативности конъюнкции
- закон ассоциативности конъюнкции
7. 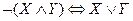 и
и 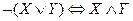 - законы де Моргана
- законы де Моргана
8. 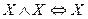 и
и 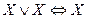 - законы сокращений
- законы сокращений
9. и еще с десяток тождественно истинных и тождественно ложных высказываний.
Пример 1. Упростить логическую формулу
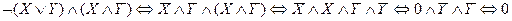
Пример 2. Доказать законы де Моргана, построив соответствующие таблицы истинности.
| X | Y | 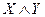 | 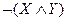 | 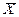 | 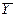 | 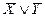 | 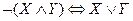 |
Таким образом, результат, выражаемый последним столбцом таблицы, свидетельствует, что высказывание 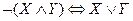 является тождественно истинным (выполняется при любых комбинациях значений входящих в него высказываний), т.е. оно действительно является логическим законом. Так же доказывается второй закон де Моргана.
является тождественно истинным (выполняется при любых комбинациях значений входящих в него высказываний), т.е. оно действительно является логическим законом. Так же доказывается второй закон де Моргана.
СИСТЕМЫ СЧИСЛЕНИЯ
Под системой счисления понимается совокупность приемов и правил представления чисел в виде конечного числа символов. Система счисления имеет свой алфавит –упорядоченный набор символов (цифр) и совокупность операций образования чисел из этих символов. Различают непозиционные и позиционные системы счисления. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных – не зависит.
Римская непозиционная система счисления. Алфавит включает символы I (1), V (5), X (10), L (50), C (100), D(500), M (1000). Значение числа, представленного в римской системе, определяется как сумма или разность цифр в числе, при этом, если меньшая цифра стоит перед большей цифрой, то она вычитается из последней, если после – прибавляется. Например, десятичное число 1998 в римской системе имеет вид MCMXCVIII. Непозиционные системы сложны и громоздки при записи чисел и мало удобны при выполнении арифметических операций.
Среди позиционных систем наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы. До сих пор используются отголоски 60 –ричной и 12 – ричной систем (в 1 минуте 60 секунд, в 1 часе 60 минут, часто применяется дюжина -12, в круге содержится 30 дюжин градусов, в сутках две дюжины часов, 1 фут равен 12 дюймам и т.д. ).
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Каждая позиционная система характеризуется своим алфавитом цифр и основанием (2, 8, 10, 16). Основание системы равно количеству цифр используемого алфавита. В качестве алфавита берутся последовательные целые числа 0, 1, 2….(p-1). Если система счисления требует использования цифр больших 9, то применяются буквы латинского алфавита (например, в 16- ричной системе это буквы A, B, C, D, E, F). Арифметические действия над числами в системе с любым основанием выполняются по тем же правилам, что и в наиболее привычной для нас десятичной системе, с той только разницей, что надо применять те таблицы сложения и умножения, которые справедливы для данной системы счисления.
Само число 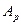 в произвольной p - ичной системе счисления (основание системы равно p) представляется в следующем виде
в произвольной p - ичной системе счисления (основание системы равно p) представляется в следующем виде
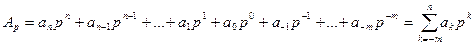 , (1)
, (1)
при этом число 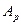 изображается как последовательность цифр
изображается как последовательность цифр 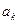 , т.е.
, т.е.
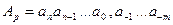 .
.
Целесообразно рассмотреть следующие задачи:
1. Перевод чисел в десятичную систему из других систем (двоичной, восьмеричной, шестнадцатеричной).
Эта задача решается наиболее просто: процедура сводится к вычислению многочлена в правой части (1) в десятичной системе.
Например, 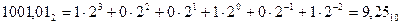 .
.
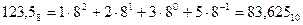
2. Перевод чисел из десятичной системы в двоичную, восьмеричную, шестнадцатеричную системы.
Перевод целой части числа осуществляется делением этой части числа на основание системы, в которую выполняется перевод, а дробной части – ее умножением на основание системы. При этом обе операции выполняются в десятичной системе.
Пример 1.Перевести число 23 из десятичной системы в двоичную систему:
| -22 | |||
| -10 | |||
| 1 | - 4 | ||
| 1 | - 2 | ||
| 1 | |||
| 0 |
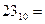
=101112 (собираются остатки от деления на 2 в порядке, обратном их получению).
Пример 2. Перевести число 0.24 из десятичной системы в пятеричную систему:
0.2410 = 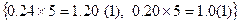 =0.115 (умножается дробная часть числа на основание системы, равное в нашем примере 5, дробная часть полученного произведения снова умножается на 5 и т.д., а затем собираются целые части полученных произведений в порядке их получения).
=0.115 (умножается дробная часть числа на основание системы, равное в нашем примере 5, дробная часть полученного произведения снова умножается на 5 и т.д., а затем собираются целые части полученных произведений в порядке их получения).
Пример 3.Перевести число 0.24 из десятичной системы в шестнадцатеричную систему:
0.2410= 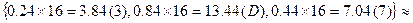 0.3D716
0.3D716
3. Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы и обратный перевод.
Эту операцию проводят с использованием триад и тетрад (три и четыре разряда в двоичном представлении числа). Для перевода числа из двоичной системы в восьмеричную число разбивают на триады влево о вправо от запятой, и в случае, когда последняя триада оказывается неполной, она дополняется нулями: для целой части – слева до трех разрядов, а для дробной части – справа. Затем каждая триада заменяется восьмеричной цифрой. Аналогично для перевода числа из двоичной системы в шестнадцатеричную число разбивают на тетрады, и каждая тетрада заменяется шестнадцатеричной цифрой.
Пример 1.Перевести число из двоичной системы в восьмеричную.
10011100,10012=010’011’100,100’1002=234,448
Обратный перевод осуществляется заменой каждой цифры триадой или тетрадой.
В задачах индикации данных в десятичном представлении оказывается удобной двоично-десятичная система счисления. В этой системе десятичные цифры от 0 до 9 представляются двоичными комбинациями от 0000 до 1001.
При работе с отрицательными числами удобна двоичная дополнительная или обратная арифметика.
В современной вычислительной технике используется в основном двоичная система счисления. Ее главное преимущество состоит в том, что практическая реализация устройств, построенных на базе этой системе, возможно при использовании технических устройств лишь с двумя устойчивыми состояниями (материал намагничен или размагничен, заряд есть или нет, отверстие есть или нет и т.д.). В результате обеспечивается высокая надежность, помехоустойчивость систем, появляется возможность применять хорошо разработанный аппарат булевой алгебры и существенно упрощается выполнение арифметических операций. Главный недостаток двоичной системы - большое число разрядов при записи больших чисел.
Следует отметить, что с точки зрения построения кодов для устройств передачи, хранения и преобразования данных наиболее экономичной является система счисления с основанием 3. При этом произведение количества различных символов в алфавите системы и количества разрядов оказывается минимальным.
ЕДИНИЦЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ НА СИНТАКСИЧЕСКОМ УРОВНЕ
Существуют меры информации синтаксического, семантического и прагматического уровней. В нашем курсе нас будет интересовать прежде всего мера информации синтаксического уровня.
На этом уровне содержательная сторона информации не имеет значения. Для измерения информации вводятся два параметра: объем информации (данных) V (объемный подход) и количество информации S (энтропийный подход).
При объемном подходе учитывается, что информация (по сути - данные) передается в виде некоторого сообщения, состоящего из совокупности символов какого-либо алфавита. Если количество информации, содержащейся в сообщении из одного символа, принять за единицу, то полное количество информации в сообщении равно количеству символов в нем. В двоичной системе счисления единицей измерения информации является бит (bit – binary digit – двоичный разряд). Тогда сообщение, состоящее из n-разрядного двоичного числа, имеет объем V=n бит.
Энтропийный подход к измерению информации основан на том, что факт получения наблюдателем информации о каком-то источнике этой информации связан, вообще говоря, с уменьшением неопределенности (энтропии) состояния источника с позиции наблюдателя. Пусть источник информации может находиться в N различных равновероятных состояниях. В качестве единицы измерения информации принято такое ее количество, которое уменьшает неопределенность знания о состоянии источника в 2 раза. Такая единица носит уже введенное выше название бит. Тогда
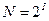 или
или 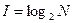 .
.
Примеры. 1. Бросание четырехгранной пирамиды. N=4, I=2 бита. Бросок кости сообщает наблюдателю количество информации, равное 2 битам.
2. Шахматный пешечный дебют. N=16, I=4 бита – столько информации несет первый ход.
Байт - 1 байт равен 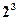 = 8 битам. Слово - 2 взаимосвязанных байта, удвоенное слово- 4 байта, учетверенное слово – 8 байт (64 бита).
= 8 битам. Слово - 2 взаимосвязанных байта, удвоенное слово- 4 байта, учетверенное слово – 8 байт (64 бита).
Кратные байту единицы - Кбайт, Мбайт, Гбайт, Тбайт .
ИСТОРИЧЕСКАЯ СПРАВКА
Компьютер – это электронное устройство для автоматизации процессов создания, хранения, воспроизведения, обработки и транспортировки данных. Компьютер представляет собой комплекс аппаратного и программного обеспечения.
Механические предшественники.
«Суммирующие часы» Вильгельма Шикарда(1623 г., Германия).
Калькулятор Блеза Паскаля (1642 г., Франция).
Калькулятор Готфрида Вильгельма Лейбница (1673 г., Германия).
Аналитическая машина Чарльза Бэббиджа (1832 г., Англия). Впервые реализован принцип разделения информации на команды и данные (склад и мельница). Огаста Ада Лавлейс – ей принадлежит идея использования перфорированных карт для программирования вычислительных операций.
Вычислительная техника на основе электромагнитных реле. Счетно-перфорационные комплексы Г.Холлерита (1887 г.) для обработки результатов переписи населения, универсальные вычислительные машины с программным управлением (модель Z-3 К. Цузе,1941 г., модель MARK-2 Г. Айкена, 1947 г.).
Математические основы электронных устройств. Двоичная система Лейбница и математическая логика Джорджа Буля (создатель логической алгебры или булевой алгебры) (первая половина XIX века, Англия).
Первая ЭВМ – на электронных лампах (1946 г., США, ENIAC, вес – 30 тонн, 18 тыс. электронных ламп, мощность 140 кВт, размеры: 4 x 30 x 6 м, 5000 операций сложения/с, оперативная память – 600 бит, проработала почти 10 лет).
Первая отечественная ЭВМ - на электронных лампах (1950 г., СССР, МЭСМ, 5000 операций сложения/с, оперативная память – 1800 бит).
Первый персональный компьютер (1976 г., фирма Apple, частота процессора 1 МГц, оперативная память – 48 Кбайт).
Персональный компьютер IBM – IBM PC/XT (1983 г., процессор Intel 8086, частота процессора 10 МГц, оперативная память – 640 Кбайт, НЖМД – 10 Мбайт, НГМД – 360 Кбайт).
Информационные революции.
В истории цивилизации выделяют несколько информационных революций, в ходе которых существенно менялись средства и способы хранения и распространения информации, доступность информации активной части населения.
Первая информационная революция. Около 10 тыс. лет до н.э. Появление языка и членораздельной речи.
Вторая информационная революция. Появление письменности. Письменность шумеров – 5 тыс. лет назад, алфавит в Греции – 700 лет до н.э.
Третья информационная революция. Изобретение книгопечатания. Первая книга появилась в Китае в конце VII в.
Четвертая информационная революция. Связана с широким распространением электрической связи в виде телеграфа, телефона, радио. Началась в конце XIX в. Здесь же надо упомянуть фотографию (1839 г.), фонограф Эдисона (1889 г.) и кино (1895 г.). Вершина этой революции – телевидение (!933 г).
Пятая информационная революция. Появление в середине XX в. электронной цифровой вычислительной техники. Предыдущие революции развивали средства хранения и распространения информации. Пятая революция привела к небывалому развитию средств и способов обработки информации.
