Непосредственные умозаключения по логическому квадрату, умозаключения обращения, превращения и противопоставления.

ТЕМА №16

Quot;Непосредственное умозаключения".

План:

Понятие непосредственного вывода. 2. Непосредственные умозаключения по логическому квадрату, умозаключения обращения, превращения и противопоставления.

1. Понятие непосредственного вывода.
По числу посылок различают непосредственные и опосредованные умозаключения. Непосредственные умозаключения состоят из одной посылки и заключения. Таковыми являются, например, все заключения по логическому квадрату, умозаключения обращения, превращения, противопоставления. Опосредованные состоят из двух и более посылок и заключения. Приведенный выше пример является опосредованным выводом, а непосредственным будет, например, умозаключение обращения:

Все планеты Солнечной системы – небесные тела

Некоторые небесные тела входят в Солнечную систему

Непосредственные умозаключения по логическому квадрату, умозаключения обращения, превращения и противопоставления.

Обращение – одна из них. Логический смысл данной операции заключается в том, что субъект (S) и предикат (Р) суждения меняются местами, не меняя качества суждения. Количество может как сохраняться (при чистом обращении), так и меняться (обращение с ограничением).
Общая структура этой операции такова:

S есть (не-есть) Р

Р есть (не-есть) S

Читается: «если S есть (не-есть) Р, то Р есть (не-есть) S».

С учетом распределенности терминов, суждения типа А, Е, I, О обращаются следующим образом:

I. А → I.

Суждение А обращается в суждение I: «Если все S есть Р, то некоторые Р есть S». Это обращение с ограничением. Ограничение связано с тем, что понятия S и Р взяты в разном объеме. В этом легко убедиться при помощи схемы:

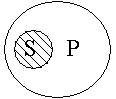Например: «Если все калькуляторы (S) являются вычислительными устройствами (Р), то лишь некоторые вычислительные устройства (Р) являются калькуляторами (S)».

II. Е → Е.

Суждение Е обращается в суждение Е без ограничения: «Если ни одно S не-есть Р, то ни одно Р не есть S». Схематически это выглядит так:

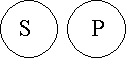
Подумаем... Проиллюстрируем это на собственных примерах.

III. I → I.

Суждение I обращается в I также без ограничения, т.е. с сохранением качества и количества суждения: «если некоторые S есть Р, то некоторые Р есть S» Схематически это доказывается так:

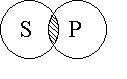Например: «Если некоторые, знающие языки программирования (S), являются студентами БГУИР (P), то некоторые студенты БГУИР (P) знают языки программирования (S)».

IV. О → .

Суждение О не обращается.

Превращение – логическая операция с простыми суждениями, в ходе которой меняется качество суждения (утвердительная связка заменяется на отрицательную и наоборот), субъект и предикат остаются на своих местах (не обращаются), а предикат исходного суждения заменяется на противоречивый в превращенном суждении.

Общая структура операции превращения:

S есть (не-есть) Р

S не-есть (есть) не-P

«Если S есть (не-есть) Р, то S не-есть (есть) не-P».

Вид исходного суждения	Вид превращенного суждения
А «Все S есть Р»	Е «Все S не-есть не-Р»
Е «Все S не-есть Р»	А «Все S есть не-Р»
I «Некоторые S есть Р»	О «Некоторые S не-есть не-Р»
О «Некоторые S не-есть Р»	I «Некоторые S есть не-Р»

В результате превращения простых категорических суждений получается:

Противопоставление.

Противопоставление – логическая операция с простыми суждениями, включающая и обращение, и превращение суждений. Делать это можно в разной последовательности. Либо вначале исходное суждение обращается («Все S есть Р» → «Некоторые Р есть S»), а затем обращенное суждение превращается («Некоторые Р есть S» → «Некоторые Р не-есть не-S»). Либо вначале исходное суждение превращается («Все S есть Р» → «Все S не-есть не-Р»), а затем превращенное суждение обращается

(«Все S не-есть не-Р» → «Все не-Р не-есть S»).

В первом случае в результате получается противопоставление субъекту (S). Во втором – противопоставление предикату (P).

Упражнения:

1.Укажите вид следующих умозаключений:
1.1. Все планеты Солнечной системы - небесные тела.
Некоторые небесные тела входят в Солнечную систему - достоверное.
1.2. Ни один вулкан не является безопасным.
Следовательно, все вулканы являются. небезопасными - достоверное.
1.3. Все христиане не являются язычниками .
Следовательно, некоторые не язычники – христиане - достоверное.
2. Проверьте правильность следующих непосредственных умозаключений по логическому квадрату:

2.1.Если верно, что все квадраты являются равносторонними прямоугольниками, то неверно, что некоторые квадраты не являются равносторонними прямоугольниками. - Ложно
2.2. Если неверно, что ни одно преступление не раскрывается, то также неверно и то, что все преступления раскрываются.- Ложно
2.3. Если неверно, что все импрессионисты - французы, то следует признать, что некоторые из них не были французами.- Истинно
2.4. Если верно, что некоторые писатели являются лауреатами Нобелевской премии, то также верно и то, что некоторые из писателей ими не являются. - Истинно

Литература:

1. 1 Светлов В.А. Современная логика: Учебное пособие. - СПб.: Питер, 2006.

2. Ивлев Ю.В. Логика: Учебник. – М.: Проспект, 2008.

3. Ивин А.А. Логика и теория аргументации: Элементарный курс: Учебное пособие для вузов. – М.: Гардарики, 2007.

4. Бочаров В.А., Маркин В.И. Основы логики: Учебник. –М.: Инфра-М, Форум, 2009.

5. Гетманова А.Д. Логика: Учеб. для студентов вузов/А.Д.Гетманова. – 8-е изд. – М.: Омега-Л, 2005.

6. Челпанов Г.И. «Учебник логики» — Изд. 11-е, доп., М.: URSS, 2009 http://www.krotov.info/lib_sec/shso/37_chelpanov.html

7. Маслов Н.А. Логика: Учебник для вузов. – Ростов н/Д: Феникс, 2007.

8. Мареев С.Н. Логика: Учебник для вузов. – Изд. 3-е, испр. и доп. – М.: Экзамен, 2009.