Обоснование метода ВЛП-резолюции

В § 4 введено декларативное определение корректности ответной подстановки. Рассмотрим механизм отыскания корректных ответных подстановок [8]. В него заложен некоторый вариант резолюционного метода опровержения, развивающий метод резолюции из [4] и называемый ВЛП-резолюцией [9, 10] (SLD-resolution – Линейная резолюция с правилом Выбор для Программных дизъюнктов).

Правилом выбора называется функция из множества целей в множество атомов, имеющая в качестве своего значения на каждой цели некоторый атом этой цели, называемый выбранным атомом.

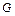Пусть – программа, – цель, – правило выбора. ВЛП-вывод для 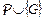посредством состоит из (конечной или бесконечной) последовательности целей, последовательности вариантов программных дизъюнктов (из и последовательности но-унификаторов, причём каждое выводимо из и посредством и Последнее означает: если есть цель и – вариант дизъюнкта из вида то называется выводимым из и посредством но-унификатора и 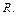если выполняются следующие условия:

а) 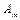– выбранный (посредством ) атом

б) (т.е. – но-унификатор для ),

в) есть цель

В терминологии метода резолюции есть резольвента для и Каждое есть подходящий вариант соответствующего программного дизъюнкта так что и не имеют общих переменных.

Опровержением (ВЛП-опровержением) для 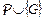посредством называется вывод, содержащий в последовательности целей пустой дизъюнкт. Этот дизъюнкт по необходимости – последняя цель в этом выводе. Если □, то говорят, что опровержение имеет длину

Пример 13. Для программы и цели 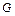из примера 1 примем в качестве правило выбора из текущей цели первого (слева) атома. Набор следующих трёх последовательностей является ВЛП-опроверже-

нием для

□;

(см. пример 1),

Только ВЛП-выводом (но не опровержением) является следующий текст:

Структура опровержения иллюстрируется рис. 2.

Множеством успехов программы называется множество всех таких, что имеет опровержение (с использованием правила выбора, зависящего от ).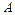

-ответной подстановкой 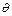для 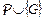называется всякая подстановка, которая может быть получена ограничением композиции на переменные из где – последовательность но-унификаторов, использованных в некотором опровержении для 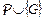посредством

Следующая теорема обосновывает метод ВЛП-резолюции.

Теорема 3. Каждая -ответная подстановка для 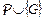является корректной ответной подстановкой.

Пример 14. Образуем композицию но-унификаторов, использованных в опровержении из примера 13. Получим Ограничение этой композиции на переменные из 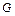есть Это и есть -ответная подстановка для По теореме 3 она корректна.

Полнота метода ВЛП-резолюции устанавливается следующей теоремой.

Теорема 4. Для каждой корректной ответной подстановки 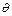множества 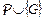существует правило выбора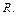 -ответная подстановка для 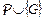и некоторая подстановка 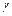такие, что 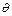совпадает с композицией

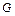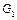Пример 15. Пусть программа состоит из одного факта и а цель есть Для любого правила выбора вариант дизъюнкта например, вида в совокупности с потребует, например, подстановки после чего цель оказывается пустой. Рассматривая произвольно другие варианты и строя но-унификаторы для и , будем получать либо вида либо где – переменная из подстановки образующей подходящий вариант на базе дизъюнкта т.е. Не будет в качестве - ответной подстановки получаться подстановка которая тем не менее является корректной ответной подстановкой, так как есть логическое следствие программы ( выводимо из ). Подстановкой о которой идет речь в теореме 4, будет либо либо Действительно, в первом случае и -ответной подстановкой будет При этом Во втором случае совпадает с композицией после её ограничения на переменные из

Из теорем 3 и 4 вытекают сформулированные ниже следствия.

Следствие 2. Множество 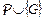невыполнимо тогда и только тогда, когда для него существует опровержение.

Следствие 3. Множество успехов программы равно её наименьшей э-модели Более того, если и имеет опровержение длины , то

Пример 16. Длина опровержения множества где – программа из примера 1, а равна 3 ( □, см. пример 13). По следствию 3 Действительно, Ø, (Ø)

Этот пример, в частности, показывает, что из при некотором не следует с необходи-

мостью существование для ВЛП-опровержения длины

Упражнения:

18. Убедитесь непосредственно, что где – программа из примера 15, (при длине опровержения тоже равной 1).

19. Пусть – программа, 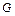– цель. Приведите ещё один пример корректной ответной подстановки, которая не может быть получена как -ответная подстановка для 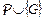ни при каком правиле выбора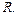

20. Пусть – программа, – атом с переменными Доказать эквивалентность следующих утверждений:

а) общезначимо,

б) невыполнимо, где – константы, не встречающиеся в или

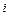в) существует опровержение для с подстановкой в качестве -ответной подстановки.