Едостаток рассматриваемого способа в том, что в цепь распространения сигнала вносится дополнительная задержка, что не всегда допустимо.

Схема с использованием дублирования перегружаемого элемента представлена на рис.7.в. Количество p дополнительных элементов, выполняющих ту же функцию, что и k-й элемент, определяется по формуле:

p > К_раз

При таком способе обеспечения К_раз дополнительная задержка не вносится, но увеличивается нагрузка на элементы, формирующие сигналы 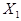и 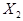, что может привести к перегрузке этих элементов и введению дополнительных элементов для обеспечения заданного К_раз

1.5. СИНТЕЗ КС С УЧЕТОМ ОГРАНИЧЕНИЯ НА К_об.

Представлению функции в виде ДНФ соответствует двухуровневая КС (если считать, что на ее вход могут поступать как прямые так и инверсные входные сигналы), на первом уровне которой элементы И, а их выходы объединяются на втором уровне элементом ИЛИ. Такое построение КС обеспечивает ее максимальное быстродействие, так как ранг схемы минимален. Однако, не всегда возможно на первом уровне и, особенно, на втором выбрать логические элементы с требуемым К_об, т.к. может оказаться, что ЛЭ с таким К_об не выпускаются промышленностью. В этом случае необходимо с помощью нескольких элементов с меньшим К_об получить эквивалент с большим К_об либо, что предпочтительней, преобразовать БФ, перейдя от ДНФ к скобочной форме. Этот переход сопровождается уменьшением К_об логических элементов, требуемого для построения схемы. Осуществить такой переход можно с помощью факторного алгоритма, суть которого рассмотрим на примере.

Пусть задана некоторая булева функция в виде

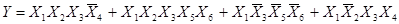
Для реализации этой функции по приведенному выражению необходимо использовать 3 логических элемента 4И, один логический элемент 5И, один логический элемент 4ИЛИ.

С помощью факторного алгоритма получим скобочную форму для заданной функции. Для этого обозначим все конъюнкции буквами:

,

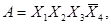
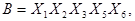
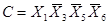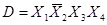
и будем рассматривать их как некоторые множества. Находим попарные пересечения множеств:

, , , , , .

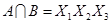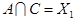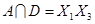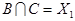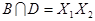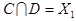Полученные пересечения показывают общие части отдельных конъюнкций. Выбираем пересечение, которое имеет наибольшую длину (если такое отсутствует, то выбирают то, которое чаще всего встречается). В данном случае это 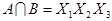. Поэтому из конъюнкций А и В выносим общую часть 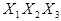. Тогда имеем:

.

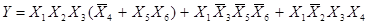Обозначим F = 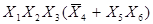и находим пересечения:

, ,

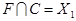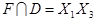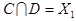
Следовательно, для исходной функции имеем:

.

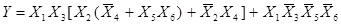Обозначим ,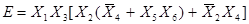

Пересечение 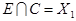. Следовательно, окончательно имеем:

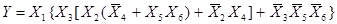
Для реализации функции по последнему выражению необходимо 5 элементов 2И, 1 элемент 3И, 3 элемента 2ИЛИ (рис.8).

Как видно из полученной схемы для ее реализации необходимы элементы с К_об = 2 или 3 (в отличие от исходной с К_об = 4 или 5). Однако ранг схемы увеличился до 7, что приводит к увеличению задержки срабатывания схемы.