Перации над нечеткими отношениями

Операции над нечеткими отношениями аналогичны соответствующим операциям для обычных отношений. Однако, как и для нечетких теоретико-множественных операций, они могут выполняться различными способами. Ниже приводятся определения операций над нечеткими отношениями с использованием треугольных нормы и конормы (см. раздел 1.3).

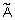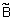Определение 38.Пересечением нечетких отношений и , заданных на , называется нечеткое отношение 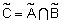с функцией принадлежности 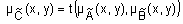, , 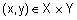где 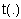‑ t-норма.

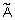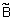Определение 39.Объединением нечетких отношений и , заданных на , называется нечеткое отношение 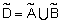с функцией принадлежности 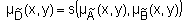, , 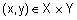где 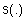‑ s-норма (t-конорма).

Пересечение и объединение нечетких отношений " приблизительно равно " и" намного меньше, чем "из примеров 5 и 6 показаны на рис. 12. В качестве t-нормы и s-нормы использовались операции нахождения минимума и максимума, соответственно.

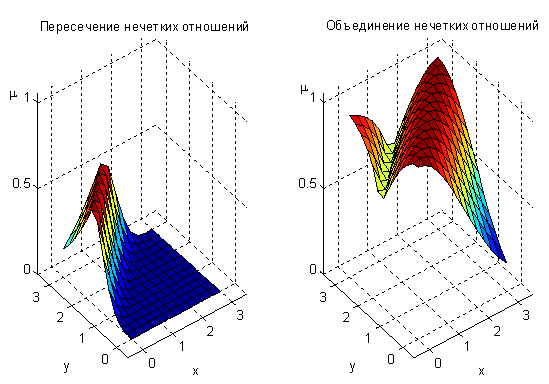
Рисунок 12 -Операции над нечеткими отношениями из примеров 5 и 6

Определение 40.Дополнением нечеткого отношения , заданного на , называется нечеткое отношение 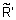с функцией принадлежности , .

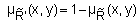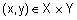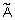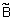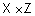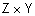Определение 41.Максминной композицией (произведением) нечетких отношений и , заданных на и , называется нечеткое отношение 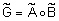на множестве с функцией принадлежности 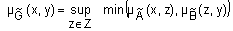, , 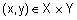, 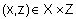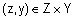. В случае конечных множеств 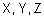матрица нечеткого отношения 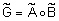получается как максминное произведение матриц 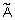и 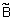. Эта операция выполняется как обычное произведение матриц, в котором операция поэлементного умножения заменена на нахождение минимума, а суммирование - на нахождение максимума. Аналогично определяются операции минимаксной и максимультипликативной композиции. Композиция играет ключевую роль в нечетком логическом выводе.

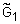Пример 8.Заданы нечеткие отношения и . Тогда максминная ( ), минимаксная ( 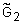) и максимультипликативная ( 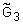) композиции этих нечетких отношений определяются такими матрицами: ; ; .

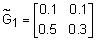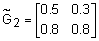Определение 42.Нечеткое отношение на называется транзитивным, если 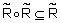.Другими словами, для любой пары 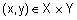степень выполнения отношения должна быть не меньше степени выполнения отношения .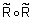

Определение 43.Транзитивным замыканием нечеткого отношения называется следующее отношени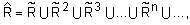е , где .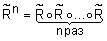

ечеткая логика

Нечеткая логика это обобщение традиционной аристотелевой логики на случай, когда истинность рассматривается как лингвистическая переменная, принимающая значения типа: "очень истинно", "более-менее истинно", "не очень ложно" и т.п. Указанные лингвистические значения представляются нечеткими множествами.

ингвистические переменные

Напомним, что лингвистической называется переменная, принимающая значения из множества слов или словосочетаний некоторого естественного или искусственного языка. Множество допустимых значений лингвистической переменной называется терм-множеством. Задание значения переменной словами, без использования чисел, для человека более естественно. Ежедневно мы принимаем решения на основе лингвистической информации типа: "очень высокая температура"; "длительная поездка"; "быстрый ответ"; "красивый букет"; "гармоничный вкус" и т.п. Психологи установили, что в человеческом мозге почти вся числовая информация вербально перекодируется и хранится в виде лингвистических термов. Понятие лингвистической переменной играет важную роль в нечетком логическом выводе и в принятии решений на основе приближенных рассуждений. Формально, лингвистическая переменная определяется следующим образом.

Определение 44.Лингвистическая переменная задается пятеркой 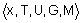, где - ; имя переменной; - ; терм-множество, каждый элемент которого (терм) представляется как нечеткое множество на универсальном множестве 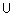; 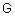- ; синтаксические правила, часто в виде грамматики, порождающие название термов; 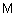- ; семантические правила, задающие функции принадлежности нечетких термов, порожденных синтаксическими правилами .

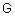Пример 9.Рассмотрим лингвистическую переменную с именем 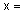"температура в комнате". Тогда оставшуюся четверку 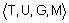можно определить так:

• универсальное множество - ; ;
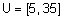• терм-множество - ; 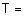{"холодно", "комфортно", "жарко"} с такими функциями принадлежностями ( ):
• 

·

·

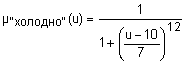
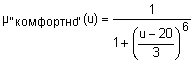
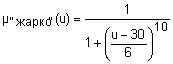
· синтаксические правила , порождающее новые термы с использованием квантификаторов "не", "очень" и "более-менее";

· семантические правила 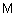, в виде таблицы 4.

Таблица 4 - Правила расчета функций принадлежности

Квантификатор	Функция принадлежности ( )
не t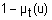
очень t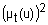
более-менее t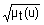

Графики функций принадлежности термов "холодно", "не очень холодно", "комфортно", "более-менее комфортно", "жарко" и "очень жарко" лингвистической переменной "температура в комнате" показаны на рис. 13.

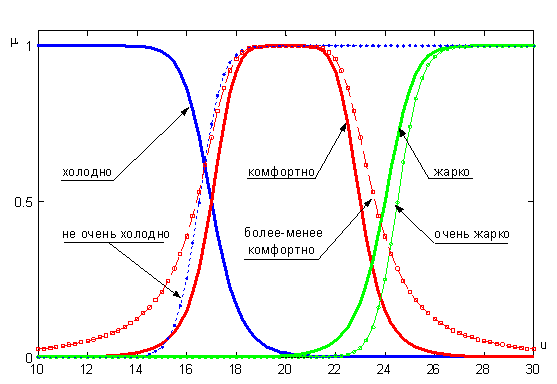
Рисунок 13 - Лингвистическая переменная "температура в комнате"

ечеткая истинность

Особое место в нечеткой логике занимает лингвистическая переменная "истинность". В классической логике истинность может принимать только два значения: истинно и ложно. В нечеткой логике истинность "размытая". Нечеткая истинность определяется аксиоматически, причем разные авторы делают это по-разному. Интервал [0, 1] используется как универсальное множество для задания лингвистической переменной "истинность". Обычная, четкая истинность может быть представлена нечеткими множествами-синглтонами. В этом случае четкому понятию истинно будет соответствовать функция принадлежности 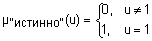, а четкому понятию ложно - ; , .

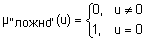Для задания нечеткой истинности Заде предложил такие функции принадлежности термов "истинно" и "ложно":

;

, ,

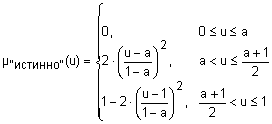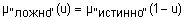где 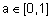- ; параметр, определяющий носители нечетких множеств "истинно" и "ложно". Для нечеткого множества "истинно" носителем будет интервал 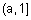, а для нечеткого множества ложно" - ; .

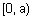Функции принадлежности нечетких термов "истинно" и "ложно" изображены на рис. 14. Они построены при значении параметра 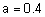. Как видно, графики функций принадлежности термов "истинно" и "ложно" представляют собой зеркальные отображения.

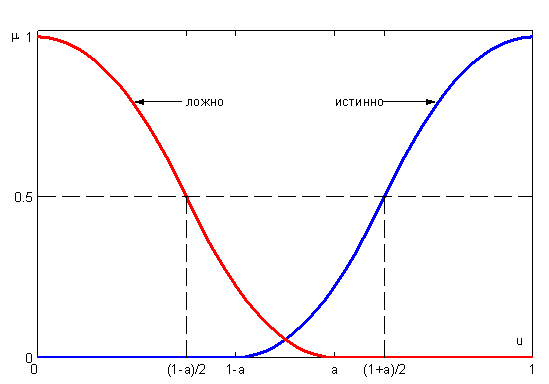
Рисунок 14 - Лингвистическая переменная "истинность" по Заде

Для задания нечеткой истинности Балдвин предложил такие функции принадлежности нечетких "истинно" и "ложно":

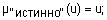
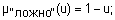
где .

Квантификаторы "более-менее" и "очень" часто применяют к нечеткими множествами "истинно" и "ложно", получая таким образом термы "очень ложно", "более-менее ложно", "более-менее истинно", "очень истинно", "очень, очень истинно", "очень, очень ложно" и т.п. Функции принадлежности новых термов получают, выполняя операции концентрации и растяжения нечетких множеств "истинно" и "ложно". Операция концентрации соответствует возведению функции принадлежности в квадрат, а операция растяжения - возведению в степень ½. Следовательно, функции принадлежности термов "очень, очень ложно", "очень ложно", "более-менее ложно", "более-менее истинно", "истинно", "очень истинно" и "очень, очень истинно" задаются так:

;

;

;

;

.

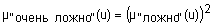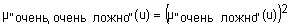
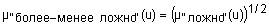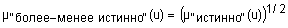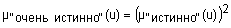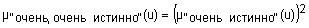Графики функций принадлежности этих термов показаны на рис. 15.

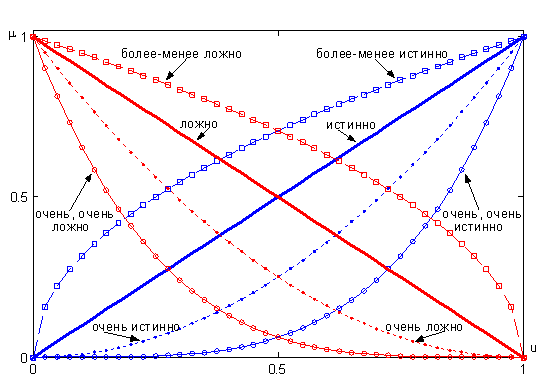
Рисунок 15 - Лингвистическая переменная "истинность" по Балдвину