Оператор примитивной рекурсии

Пусть заданы частичные функции g: Nⁿ ® N и h: Nⁿ⁺² ® N. Оператором примитивной рекурсии называется оператор, сопоставляющий паре (g, h) такую частичную функцию f: Nⁿ⁺¹ ® N, что для всех x₁,…,x_n,у Î N имеют место равенства:

f(x₁,…,x_n,0) = g(x₁,…,x_n);

f(x₁,…,x_n,y+1) = h(x₁,…,x_n,y, f(x₁,…,x_n,y)).

Поскольку область определения и значения дополняются отмеченной точкой, то равенство частичных функций означает, что для каждого значения аргумента либо левая, либо правая части равенства определены и равны между собой, либо обе его части не определены. Значение оператора примитивной рекурсии обозначается: f = R(g,h). Если g и h определены всюду, то f = R(g,h) определена всюду.

Если n = 0, то для любых числа g Î N и частичной функции h: N² ® N частичная функция f = R(g,h) определяется с помощью равенств:

f(0) = g, f(y + 1) = h(y,f(y)).

Функция f называется примитивно рекурсивной, если ее можно получить из простейших функций s, 0 и Iⁿ_m с помощью операторов композиции и примитивной рекурсии (таким образом, примитивно рекурсивная функция всюду определена.)

Пример 2

Функция o: N ® N, принимающая постоянные значения o(x)=0, будет примитивно рекурсивной в силу

o(0) = 0;

o(y+1)= I²₂(y, o(y)).

Функция оⁿ: Nⁿ ® N, все значения которой равны нулю, примитивно рекурсивна, ибо она является композицией о ° Iⁿ₁ простейших функций Iⁿ₁: Nⁿ ® N и о: N ® N. Рассмотрим при k ³ 1 функцию c_k: Nⁿ ® N, все значения которой равны k. Функция c_k равна композиции функций оⁿ: Nⁿ ® N и k функций N ® N ®…® N, каждая из которых равна s, c_k = s^k °oⁿ. Стало быть, c_k примитивно рекурсивна.

Пример 3

Функция f: N² ® N, заданная как f(x,y) = x + y, удовлетворяет соотношениям:

f(x,0) = x;

f(x,y + 1) = (x + y) +1 = f(x,y) + 1 = s(f(x,y)).

Положим: g(x) = I¹₁(x) = x, h(x,y,z) = s(z). Так как f(x,0) = g(x) и
f(x,y + 1) = h(x,y,f(x,y)), то f = R(g,h) = R(I¹₁,s ° I³₃). Значит, f – примитивно рекурсивна.

Предложение 1 Для любых примитивно рекурсивных функций f(x₁, …, x_n) и g(x₁, …, x_n) их сумма примитивно рекурсивна.

Доказательство. Вытекает из равенства

f(x₁, …, x_n)+g(x₁, …, x_n)= S(+,f,g) (x₁, …, x_n).

Пример 4

Функция f: N² ® N, заданная как f(x,y) = x×y, удовлетворяет соотношениям:

f(x,0) = 0;

f(x,y + 1) = x ( y + 1) = f(x,y) + x.

Положим: g(x) = o(x), h(x,y,z) = x+z . Так как f(x,0) = o(x) и
f(x,y + 1) = h(x,y,f(x,y)), то f = R(g,h) = R(o, S(+, I³₁,, I³₃). Значит, f – примитивно рекурсивна.

Предложение 2 Для любых примитивно рекурсивных функций f(x₁, …, x_n) и g(x₁, …, x_n) их произведение примитивно рекурсивно.

Пример 5

Рассмотрим функцию: f(x,y) = x^y. Поскольку f(x,0) = 1, и
f(x,y + 1) = x×f(x,y) = g(x,y,f(x,y)), где g(x,y,z) = x×z – примитивно рекурсивная функция (как композиция операции умножения и функции (I³₁, I³₃): N³ ® N²), то f(x,y) примитивно рекурсивна.

Пример 6

Пусть d(x) = max(0,x – 1). Имеют место равенства d(0) = 0 и
d(y + 1) = y = g(y,d(y)), где g(y,z) = I²₁(y,z) = y. Следовательно, d(x) – примитивно рекурсивна.

Пример 7

Пусть r(x,y) = max(0,x – y). Верны соотношения r(x,0) = x и
r(x,y + 1) = d(r(x,y)) = g(x,y,r(x,y)), где g(x,y,z) = d(z) – функция из примера 5. Значит, r(x,y) – примитивно рекурсивна.

Пример 6 показывает, что функция f(x,y) =ôx-yô= r(x,y) + r(y,x) примитивно рекурсивна, как композиция функций x₁ + x₂ и пары функций (r(x,y),r(y,x)): N² ® N² (примитивная рекурсивность функции r(y,x) получается из разложимости r(y,x) = S³(r, I²₂, I²₁)).

Оператор минимизации

Пусть g: Nⁿ⁺¹ ® N – частичная функция. Будем говорить, что частичная функция f: Nⁿ ® N получается из неё с помощью оператора минимизации,и писать:

f(x₁,…,x_n) = m y [g(x₁,…,x_n,y) = 0],

если выполнено следующее условие: f(x₁,…,x_n) определено и равно y Î N тогда и только тогда, когда значение g(x₁,…,x_n,0),…,g(x₁,…,x_n,y -1) определены и не равны 0, а g(x₁,…,x_n,y) = 0.

Частичная функция f: Nⁿ ® N называется частично рекурсивной, если она может быть получена из простейших функций 0, s, Iⁿ_m за конечное число применений операторов композиции, примитивной рекурсии и минимизации.

Пример 8

Рассмотрим примитивно рекурсивную функцию: g(x,y) = x – Sg(y), где Sg(y) = 0, при y = 0, и Sg(y) = 1, для y > 0. Тогда значения:

f(x) = m y[ôx-Sg(y)ô= 0]

не определены при x > 1. Наименьшее среди y Î N, удовлетворяющих 0 – Sg(y) = 0, будет равно 0, а наименьшее среди y, при которых 1 – Sg(y) = 0, равно 1. Следовательно, f(0) = 0, f(1) = 1, и f(x) не определены при x > 1. Функция ôx – Sg(y)ô примитивно рекурсивная, значит, f(x) – частично рекурсивная.

Пусть А – подмножество натуральных чисел. Частичной характеристической функцией множества А называется частичная функция C_A: N ® N, равная 0 в точках множества А и не определенная вне А. Множество А называется частично рекурсивным, если его частичная характеристическая функция частично рекурсивна. Множество А называется примитивно рекурсивным, если функция N ® N, равная 0 на А и равная 1 вне А, является примитивно рекурсивной.

Теорема. Пусть f: N ® N – примитивно рекурсивная функция, A Í N – примитивно рекурсивное множество. Тогда частичная функция f_A: N ® N, определенная как f_A(x) = f(x) для x Î A и неопределенная при x Ï A, является частично рекурсивной.

Доказательство. Легко видеть, что f_A(x) = f(x) + C_A(x). Поэтому f_A частично рекурсивна, как сумма частично рекурсивных функций.

Понятие частично рекурсивной функции является одним из главных в теории алгоритмов. Частично рекурсивная функция вычислима с помощью процедуры, отвечающей нашему представлению об алгоритме. С другой стороны, все известные до сих пор уточнения определения алгоритма не привели к классу вычислимых функций, который был бы шире класса частично рекурсивных. Поэтому общепринятой является следующая гипотеза:

Тезис Чёрча. Класс алгоритмически (или машинно) вычислимых частичных числовых функций совпадает с классом всех частично рекурсивных функций.

Машины Тьюринга

Рассмотрим гипотетическую «машину», имеющую конечное множество Q внутренних состояний и одну бесконечную ленту, разделенную на ячейки, по которой перемещается устройство для чтения и записи, именуемое головкой. В каждый из такт времени головка читает содержимое текущей ячейки, затем пишет в эту ячейку новый символ и перемещается влево или вправо, или остается на месте. Текущей ячейкой становится новая ячейка, она будет той, на которую указывает головка. Символы принадлежат конечному алфавиту А.

Пример 1

Алфавит состоит из цифр 0,1,…,9. На ленте написано слово:

…

…

и головка показывает на 9. Тогда в следующий такт времени головка может записать вместо 9 цифру 8 и переместиться влево. После этого она будет показывать на 0.

Перейдем к точным определениям.

Машиной Тьюринга T = (A,Q,p) называется тройка, состояний из непустых конечных множеств A = {a₀,a₁,…,a_n}, Q = {q₀,q₁,…,q_m} и частичной функции
p: Q ´ A ® Q ´ A ´ {L,S,R}.

Здесь {L,S,R} – множество, состоящее из трех элементов. Оно одинаково для всех машин Тьюринга и интерпретируется командами перемещения головки: L – влево, R – вправо, S – стоять на месте.

Множество А называется внешним алфавитом, его элементы – буквами. Буквы a₀ и a₁ для всех машин Тьюринга одинаковы: a₀ = 0, a₁ = 1. Элементы q₀,…,q_m называются внутренними состояниями.

Частичная функция p называется программой и записывается или с помощью прямоугольной таблицы, в которой в клетке (q_i,q_j) записывается тройка
p(q_i,q_j) Î Q ´ A ´ {L, S, R}, или с помощью списка команд вида:

· q_ia_j ® q_ka_e означающей (q_k,a_e,S) = p(q_i,a_j),

· q_ia_j ® q_ka_eR означающей (q_k,a_e,R) = p(q_i,a_j),

· q_ia_j ® q_ka_eL означающей (q_k,a_e,L) = p(q_i,a_j).

Эти команды обозначим через T(i,j).

Машиным словом, или конфигурацией, называется слово вида: aq_ka_eb, где
0 £ k £ m, 0 £ e £ n, a и b – слова (возможно, пустые), составленные из букв алфавита А. Для обозначения слова аа…а, в котором буква а повторяется x раз, пишем: а^х.

Машинное слово: aq_ka_eb интерпретируется как положение, при котором головка указывает на символ a_e, машина находится во внутреннем состоянии q_k, слева от текущей ячейки находятся символы, составляющие слово a, а справа – слово b. В примере 1 машинное слово равно: 20q_i931 для некоторого i.

Пусть задана машина Тьюринга Т и машинное слово M = aq_ia_jb, где 0 £ i £ m. Обозначим через M_T’ слово, которое получается (за один такт) по правилам:

1) для i = 0 положим M_T’ = M;

2) для i > 0 выполняем одно из следующих трех преобразований:

· если T(i,j) = q_ia_j ® q_ka_e, то M_T’ = aq_ka_eb;

· в случае T(i,j) = q_ia_j® q_ka_eR,

если b не пусто, то M_T’ = aq_ea_kb, иначе MT ’= aq_ea_ka₀;

· в случае T(i,j) = q_ia_j ® q_ka_eL,

если a = a₁a_s для некоторых a₁ и a_s, то MT’ = a₁q_ka_sa_eb,

иначе (т.е. если a пусто) MT’= q_ka₀a_eb (дополнительная инструкция).

Положим: M_T⁰ = M, M_T⁽ⁿ⁺¹⁾ = (M_T⁽ⁿ⁾)’.

Будем говорить, что машина Т перерабатывает машинное слово М в слово М₁, если M_T⁽ⁿ⁾ = M₁ для некоторого n ³ 0. Пишем: М Þ_T M₁, если Т перерабатывает М в М₁, и при этом не используется дополнительная инструкция (из правил образования слова M_T’).

Говорим, что машина Т вычисляет частичную функцию f: Nⁿ ® N, если выполнены следующие условия:

· если (x₁,…,x_n) Î Dom(f), то машина Т останавливается, т.е. перерабатывает слово q₁01^x10…1^xn0 в некоторое слово aq₀b, и при этом aq₀b содержит f(x₁,…,x_n) вхождений символа 1 (здесь символы x₁, … , x_n обозначены через x1, ..., xn) ;

· если (x₁,…,x_n) не принадлежит Dom(f), то машина, начиная со слова
M = q₁01^x10…1^xn0, работает бесконечно, т.е. q₀ не входит в M_T⁽ⁿ⁾ ни для каких n ³ 0.

Говорим, что машина Т правильно вычисляет частичную функцию f: Nⁿ ® N, если выполнены условия:

· если (x₁,…,x_n) Î Dom(f), то q₁01^x10…1^xn0 Þ_Tq₀01^f(x1,…,xn)0…0;

· в противном случае машина, начиная со слова q₁01^x10…1^xn0, работает бесконечно.

Частичная функция f называется (правильно) вычислимой, если существует машина Тьюринга, которая (правильно) вычисляет f.

Пример 2

Пусть машина Тьюринга T = {A, Q, p}, A = {0,1}, Q = {q₀,q₁,q₂} задана с помощью таблицы:

	q0	q1	q2
		q20R	q01S
			q21R

Рассмотрим слово: M = q₁011…10. На первом шаге выполняется команда q₁0®q₂0R. Получаем: M_T’ = 0q₂11…10. Затем, до тех пор, пока слово не превратится в слово 011…1q₂0, будет выполняться команда q₂1 ® q₂1R. После этого будет выполнена команда q₂0 ® q₀1, и машина остановится, ибо q₀ соответствует состоянию остановки. Входное слово, состоящее из x единиц, означает, что аргументом вычисляемой функции является число x. Поскольку на выходе получается x + 1 подряд идущих единиц, то машина вычисляет функцию: s(x) = x + 1.

Пример 3

Вычисление функции: s(x) = x+1 в примере 2 не является правильным. Построим машину Тьюринга для правильного вычисления:

	q0	q1	q2	q3	q4
		q20R	q31R	q40L	q00L
			q21R	q41L	q41L

Упражнение

Построить машину Тьюринга, правильно вычисляющую функцию: o(x) = 0.

Можно построить машины Тьюринга для правильного вычисления функций:

I_mⁿ(x₁,…,x_n), 1 £ m £ n.

С помощью построения различных машин Тьюринга доказывается, что операторы композиции, примитивной рекурсии и минимизации переводят правильно вычислимые функции в правильно вычислимые. Отсюда вытекает правильная вычислимость всех частично рекурсивных функций. Более того, справедливо и обратное утверждение.

Теорема 1. Частичная функция правильно вычислима тогда и только тогда, когда она частично рекурсивна.

Тезис Чёрча и алгоритмически неразрешимые проблемы

Поскольку класс частично рекурсивных функций совпадает с классом правильно вычислимых, то тезис Чёрча равносилен предположению о том, что для любой алгоритмически вычислимой функции существует правильно вычисляющая её машина Тьюринга.

Применим это для доказательства алгоритмической неразрешимости проблемы остановки машины Тьюринга, которая заключается в нахождении алгоритма, определяющего по машине Тьюринга и начальным данным, остановится ли машина через конечное число шагов. Так как машина Тьюринга задается с помощью конечного набора символов и слов, то число машин Тьюринга счетно и может быть выписано в последовательность: T₀, T₁, … .

Теорема (о проблеме остановки). Пусть T₀,T₁, T₂,… последовательность, перечисляющая все машины Тьюринга, h(n,k) – функция, принимающая значение 1, если машина T_n останавливается, начиная работу с машинного слова q₁01^k0, и принимающая значения h(n,k) = 0 в других случаях. Тогда функция h: N² ® N не является частично рекурсивной. Иными словами, нет алгоритма, определяющего, остановится ли машина Тьюринга, если на вход ей подать число k.

Доказательство. От противного. Пусть функция h(n,k) частично рекурсивна. Тогда частичная функция:

f(n) = My[h(n,n) + y = 0]

тоже частично рекурсивна. Существует номер m такой, что f правильно вычисляется с помощью машины T_m. Тогда f(m) = 0, если и только если h(m,m) = 0. Согласно определению функции h равенство h(m,m) = 0 имеет место тогда и только тогда, когда машина T_m не останавливается, начиная со слова q₁01^m0. Но f правильно вычисляется с момощью T_m , значит, T_m не остановится, начиная с m, если и только если f(m) не определено. Получаем противоречие: f(m) = 0, если и только если f(m) не определено, Следовательно, h – не частично рекурсивна.

Вычислительная сложность

Возможны различные подходы к оценке качества алгоритма, например, оценивается число команд (инструкции), из которых он состоит, число операций, объем используемой памяти. Будем считать, что алгоритм отождествляется с программой, работающей на идеальной ЭВМ, состоящей из процессора, памяти, входной и выходной лент. Ленты и память состоят из ячеек, каждая из которых может хранить двоичную запись одного числа.

Имеется два подхода к оценке времени и памяти, необходимых для выполнения программы: при равномерном весовом критерии считается, что каждая команда программы затрагивает один такт времени, и каждое число занимает одну ячейку памяти. Логарифмический весовой критерий учитывает ограниченность размера реальной ячейки памяти и основывается на предложении, что объем памяти для хранения числа n равен длине его двоичного представления l(n) = [log₂n] + 1, а время исполнения команды пропорционально длине его операндов.

Временная сложность программы – это функция f_max(n), равная наибольшей из сумм времен, затраченных на каждую выполненную команду при обработке входных данных, состоящих из n чисел. Таким образом, для каждой n-ки (x₁,…,x_n) Î D из области допустимых значений начальных данных (например, области определения частично рекурсивной функции) надо вычислить время t(x₁,…,x_n), затраченное на выполнение программы. Тогда временная сложность будет равна max{t(x₁,…,x_n):(x₁,…,x_n) Î D}. Временная сложность в среднем при равномерном критерии равна: 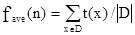, где ôDô – число элементов области D Í Nⁿ, а x = (x₁,…,x_n) – элементы из D. Временная сложность в лучшем случае равна: f_min(n) = min{t(x):x Î D}. Такие же понятия определяются для объема памяти. Вместо времени t(x₁,…,x_n) рассматривается количество u(x₁,…,x_n) ячеек памяти, к которым обращалась программа, имеющая на выходе x₁,…,x_n.

Для описания асимптотического поведения сложностных функций используется следующий формализм: Говорят, что функция f(n) не больше по порядку, чем g(n), и пишут: f(n) = O(g(n)), если существует такая константа C > 0, что почти для всех n (т.е. для всех, кроме конечного множества значений n) справедливо f(n) £ Cg(n). Функции одного и того же порядка, если f(n) = O(g(n)) и g(n) = O(f(n)).