Тверской государственный технический университет. Кафедра «Технология машиностроения»
Кафедра «Технология машиностроения»
МЕТРОЛОГИЯ,
СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ
Методические указания к лабораторной работе
для студентов специальностей
1201, 1705, 1706, 1709, 1711, 1718, 2102, 2301
Тверь 2006
Методические указания содержат общие правила по обработке результатов измерений, построению графиков с целью определения фактической точности изготовления и оценки погрешности прибора.
Даны описания принципа работы и метрологические характеристики приборов, изложена методика измерения на них.
К каждой работе даны контрольные вопросы и литература.
Методические указания утверждены и рекомендованы к опубликованию на заседании кафедры (протокол № 8 от 19.04.2006г.).
Составители: Испирян Н.В.,
Горлов И.В.,
Нестерова И.Н.
© Тверской государственный технический университет
1. Лабораторная работа № 5
ИССЛЕДОВАНИЕ ПОГРЕШНОСТЕЙ ИЗГОТОВЛЕНИЯ ВЫБОРКИ ДЕТАЛЕЙ С ПОМОЩЬЮ ИЗМЕРИТЕЛЬНОЙ ПРУЖИННОЙ ГОЛОВКИ (МИКРОКАТОРА)
Цель работы: ознакомление с устройством, приемами измерения микрокатором; определение по исследованной выборке деталей всего возможного интервала рассеивания измеряемого размера.
Вида погрешностей
При изготовлении, а так же при измерении детали неизбежны погрешности, которые делятся на систематические и случайные. Систематическими называются погрешности постоянные по величине и знаку, или изменяющиеся по какому-либо закону. Они делятся на постоянные и переменные. Постоянные систематические погрешности возникают при измерении из-за неправильной настройки прибора. Примерами переменной систематической погрешности являются величины радиального биения, вызываемого эксцентриситетом, а так же погрешность от износа инструмента при изготовления деталей.
Случайными называются непостоянные по знаку и величине погрешности, которые возникают при одновременном действии нескольких факторов. Вследствие грубых ошибок могут иметь место резко отличающиеся от основной массы результаты. Такие результаты измерений следует считать недействительными.
Инструменты и материалы для работы:
- измерительная пружинная головка (микрокатор);
- объекты измерения;
- эскизы объектов измерения;
- плоскопараллельные концевые меры длины;
- протирочные материалы.
1.1. Последовательность выполнения работы
1.1.1. Изучить устройство и приемы измерения микрокатором.
1.1.2. Выполнить эскизы измеряемых деталей.
1.1.3. Подготовить приборы к измерениям.
1.1.4. Измерить выборку деталей и результаты занести в табл. 1.1.
1.1.5. Произвести статистические расчеты и заполнить табл. 1.2. и 1.3.
1.1.6. По результатам исследований построить графики и определить количество брака.
1.2. Руководство к пользованию микрокатором
Пружинная измерительная головка имеет точный и чувствительный механизм, вследствие чего необходимо соблюдать следующие правила:
1.2.1. Защитное стекло нельзя протирать сухой тканью из-за возникающего статического электричества, влиявшего на результаты измерений. Для протирки используют слегка увлажненную ткань.
1.2.2. Высокая чувствительность прибора требует бережного отношения с ним. Прибор необходимо предохранять от ударов.
1.2.3. Подъем и опускание измерительного стержня с помощью арретира следует производить плавно.
1.2.4. Разборку прибора лицам, не имеющим отношение к ремонту, категорически воспрещается.
1.3. Устройство прибора
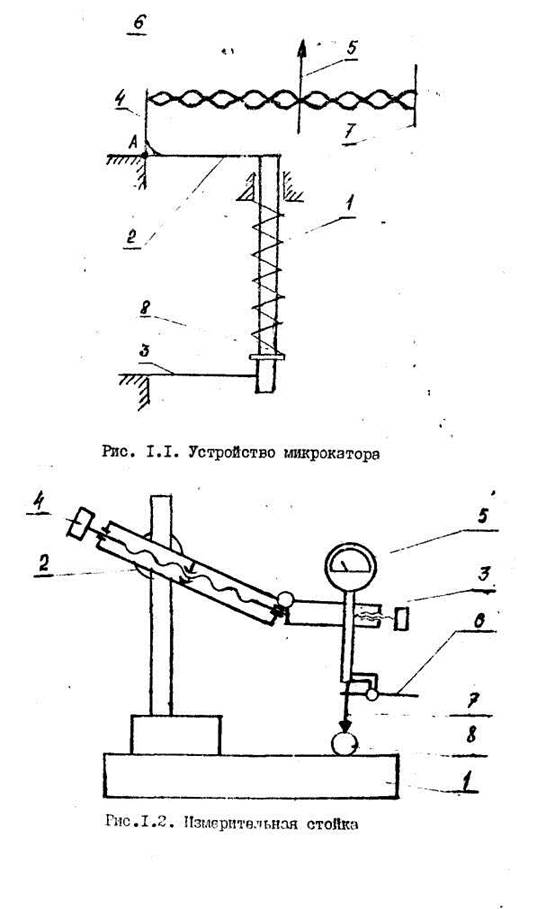
Микрокатор (рис.1.1) служит для измерения наружных размеров гладких точных деталей. По конструкции прибор является механическим; по методу измерения - сравнительным или относительным измерительным прибором.
В основу передаточного механизма микрокатора положена плоская, скрученная от середины, бронзовая пружинная лента 6. Толщина бронзовой ленты 0,004 .. .О,006 мм, ширина 0,15 ... 0,3 мм. Лента с одной стороны закреплена к неподвижному кронштейну 7, а с другой - к угольнику 4, который может поворачиваться вокруг точки А на двух плоских пружинах 2 и 3. В средней части ленты закреплена стеклянная стрелка 5.
Измерительный стержень 8 подвешен на двух плоских пружинах 2 и 3. При перемещении измерительного стержня происходят поворот угольника 4 и растяжение ленты 6, на которой поворачивается стрелка 5. Для обеспечения постоянства зажима имеется пружина I.
1.4.Настройка и измерение
Согласно настроечному размеру, набрать блок концевых мер. По блоку концевых мер настроить прибор на нуль (рис.1.2). Для этого установить блок концевых мер на столик I. Отвернул винт 2, опустить кронштейн с микрокатором 3 до зазора размером I...1,5мм относительно измерительного стержня и блока концевых мер. Затем, вращая винт 4, добиться того, чтобы на микрокаторе 5 стрелка установилась на нуль, после чего отвести и опустить арретир 6 и снова проверить настройку.
Для измерения детали необходимо извлечь блок концевых мер из-под измерительного наконечника 7, пользуясь арретиром, и поместить на его место измеряемую деталь 8.
Для определения диаметра деталь необходимо прокатывать по столику до получения максимального значения на приборе.
1.5. Обработка результатов
Таблица 1.1
Результаты измерений
| No | х | No | х | No | х | No | х |
| - 16 - 8 - 20 - 25 - 16 + 1 - 15 - 4 - 14 - 8 | - 12 - 16 - 23 - 19 - 7 - 15 - 4 - 7 - 9 - 12 | - 17 - 19 - 7 - 6 - 15 - 10 - 11 - 13 - 17 + 16 | - 11 - 16 - 19 - 21 - 11 - 13 - 16 - 19 - 18 - 28 |
Согласно полученным измерениям определяем действительное поле рассеивания:
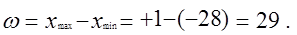 (1.1)
(1.1)
Отдельные грубые значения отклонений, резко отличающиеся из общего ряда значений, в расчет не принимают (например: + 16 в тридцатом измерении),
Поле рассеивания ω разбивают на 7 … 12 интервалов. При этом конечные предельные отклонения крайних интервалов можно выбрать округленными, несколько выходящими за отклонения 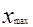 и
и 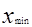 . Установленные предельные значения интервалов заносят в таблицу 1.2. После этого по таблице I.I определяют, сколько измерений попадают в каждый интервал. Число случаев, попавших в интервал, называют частотой попадания. Определив середины интервалов и частоты попадания результатов измерений в эти интервалы, заполняют таблицу 1.2. Определяем величину интервала к:
. Установленные предельные значения интервалов заносят в таблицу 1.2. После этого по таблице I.I определяют, сколько измерений попадают в каждый интервал. Число случаев, попавших в интервал, называют частотой попадания. Определив середины интервалов и частоты попадания результатов измерений в эти интервалы, заполняют таблицу 1.2. Определяем величину интервала к:
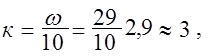 (1.2)
(1.2)
Таблица 1.2
К расчету эмпирических характеристик распределения
| Интервалы отклонений от номинального размера, мкм | Середина интервала хi, мкм | Частота ni шт. | ni хi | ni хi2 | |
| от | до | ||||
| + 1 - 2 - 5 - 8 - 11 - 14 - 17 - 20 - 23 - 26 | - 2 - 5 - 8 - 11 - 14 - 17 - 20 - 23 - 26 - 29 | - 0,5 - 3,5 - 6,5 - 9,5 - 12,5 - 15,5 - 18,5 - 21,5 - 24,5 - 27,5 | - 0,5 - 7 - 26 - 38 - 87,5 - 139,5 - 129,5 - 43 - 49 - 27,5 | 0,25 24,5 1093,75 2162,25 2395,75 924,5 1200,5 756,25 | |
| N = 39 | Σ ni хi = - 537,5 | Σ ni хi2 = 9087,75 |
Расчет статистических характеристик:
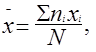 (1.3)
(1.3)
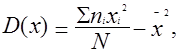 (1.4)
(1.4)
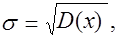 (1.5)
(1.5)
где 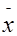 - среднее арифметическое значение случайной величины;
- среднее арифметическое значение случайной величины;
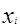 - середина интервала;
- середина интервала;
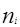 - частота попадания в интервал;
- частота попадания в интервал;
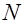 - число измерений;
- число измерений;
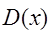 - дисперсия;
- дисперсия;
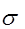 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
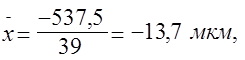
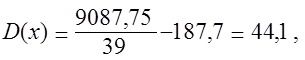
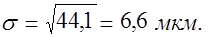
1.6. Построение полигона распределения
По значениям 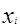 и
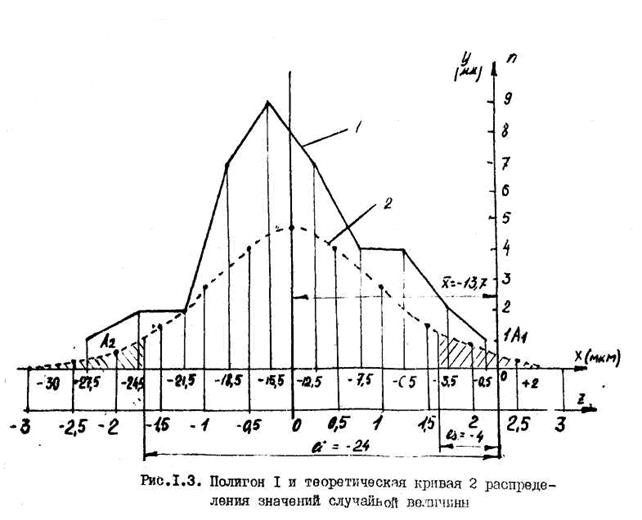
и 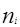 из таблицы 1.2 строят в выбранном масштабе полигон распределения (рис.1.3).
из таблицы 1.2 строят в выбранном масштабе полигон распределения (рис.1.3).
На ось абсцисс наносим, в соответствующем масштабе середины интервалов, восстанавливаем из этих значений перпендикуляры, длины которых пропорциональны 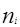 - частоте в определенном масштабе (I случай – 10 мм). Вершины перпендикуляров соединяем ломаной линией и получаем эмпирическую кривую (полигон) распределения случайной величины. На полигоне распределения строим вертикальную линию из точки, соответствующей значению
- частоте в определенном масштабе (I случай – 10 мм). Вершины перпендикуляров соединяем ломаной линией и получаем эмпирическую кривую (полигон) распределения случайной величины. На полигоне распределения строим вертикальную линию из точки, соответствующей значению 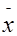 (в данном случае
(в данном случае 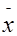 = -13,7).
= -13,7).
1.7. Построение кривой нормального распределения
Для сравнения полученного характера распределения выборки деталей с нормальным распределением строят на графике полигона кривую нормального распределения (рис. 1.3 кривая 2). Рекомендуется строить каждую ветвь кривой по шести точкам. Так как вся кривая нормального распределения укладывается по оси абсцисс в пределы ±3б, то отклонение от центра группирования 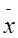 , т.е. значения z, желательно выбирать через 0,5 б по обе стороны от
, т.е. значения z, желательно выбирать через 0,5 б по обе стороны от 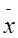 . Для каждой намеченной точки z по оси абсцисс определяют значения кратные 0,5б,а именно: 0,5; 1; 1,5; 2; 2,5; 3 . Чтобы выделить новые значения z от значений уже построенного графика, рекомендуется ось z проводить параллельно построенной оси x . Вертикальная ось для обоих графиков будет одни.
. Для каждой намеченной точки z по оси абсцисс определяют значения кратные 0,5б,а именно: 0,5; 1; 1,5; 2; 2,5; 3 . Чтобы выделить новые значения z от значений уже построенного графика, рекомендуется ось z проводить параллельно построенной оси x . Вертикальная ось для обоих графиков будет одни.
Значения плотности вероятности Уz рассчитываются по формуле:
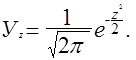 (1.6)
(1.6)
Для соответствия координат точек кривой нормального распределения и уже построенного графика по оси ординат (n и Уz) необходимо рассчитать масштабный коэффициент в:
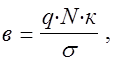 (1.7)
(1.7)
где q - масштаб частоты по оси ординат, (в данном случае q = 10, т.е. один случай соответствует 10 мм графика по этой оси);
N - число измерений, взятых в расчет;
к - величина интервала, взятого для таблицы 1.2 (в данном случае к = 3);
σ – среднее квадратичное отклонение.
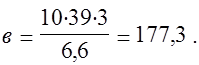
Для получения величины У в нужной масштабе необходимо сделать пересчет:
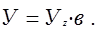 (1.8)
(1.8)
Результаты заносим в таблицу 1.3.
Таблица 1.3
Координаты теоретической кривой
Отклонение от центра группирования 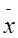 , мкм , мкм | z | Уz | У, мм |
| ± 3,3 ± 6,6 ± 9,9 ± 13,2 ± 16,5 ± 19,8 | 0,5 1,0 1,5 2,0 2,5 3,0 | 0,3989 0,3521 0,2420 0,1295 0,0540 0,0175 0,0044 | 46,8 41,3 28,4 15,2 6,3 2,0 0,5 |
По значениям z и У строим график нормального распределения.
1.8 Определение процента брака
Определение процента деталей, выходящих за верхнюю и нижнюю границу поля допуска, следует производить по статистическим характеристикам, т.к. они отражают наиболее полную картину возможных размеров детали. Определяется зона А1 - количество деталей, размеры которых выходят за верхнюю границу; и зона A2 - количество деталей, размеры которых выходят за нижнюю границу поля допуска.
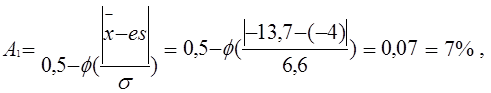 (1.9)
(1.9)
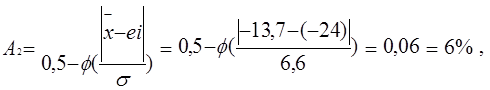 (1.10)
(1.10)
где Ф- значение интеграла вероятности нормального распределения - функция Лапласа, [1, с. 340];
es - верхнее отклонение;
еi - нижнее отклонение.
Предельные отклонения задаются преподавателем.
Зоны А1 - исправный брак и A2 - неисправный, необходимо показать на графике (рис. 1.3).
1.9. Контрольные вопросы
1.9.1. Назовите части микрокатора.
1.9.2. Объясните кинематическую схему микрокатора.
1.9.3. Объясните настройку и приемы измерения микрокатором.
1.9.4. Систематические и случайные погрешности. Приведите примеры.
1.9.5. Объясните методику обработки результатов.
1.9.6. Задача, решаемые данной методикой обработки результатов.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Якушев А. И., Воронцов Л. Н., Федотов Н. Н. Взаимозаменяемость, стандартизация и технические измерения: Учебник для вузов. - М.: Машиностроение, 1966, С. 89 ... 94, 118 ... 120.
2. Захаров В.И. Взаимозаменяемость, качество продукции и контроль в машиностроении. - Л.: Лениздат, 1990. C.113 ... 115.
2. Лабораторная работа № 6
ОПТИКО-МЕХАНИЧЕСКИЕ ПРИБОРЫ И ИССЛЕДОВАНИЕ ИХ ПОГРЕШНОСТЕЙ
Цель работы: ознакомление с устройством и приемами измерения оптиметра; определение с помощью математической статистики погрешности прибора. Инструменты и материалы для работы:
оптиметр;
плоскопараллельные концевые меры длины;
объект измерения;
авиабензин, мягкие полотняные салфетки.
2.1. Принцип работы трубки оптиметра
Оптиметр относится к группе оптико-механических приборов, основанных на применении рычажно-оптического передаточного механизма с использованием принципа автоколлимации в сочетании с качающимся зеркалом.
Оптическая система заключена в Г- образную трубку. В фокальной плоскости объектива 5 (рис. 2.1) помещена стеклянная пластина 3. На этой пластине по одну сторону от ее оси нанесена шкала, которая освещается через призму 2 от внешнего источника света. Лучи света от шкалы, пройдя призму 4 и объектив 5, падают параллельным пучком на поворотное зеркало 6. Отразившись от зеркала, лучи возвращаются обратно, собираются на пластине и дают по другую сторону от главной оптической оси, где нанесен неподвижный штрих-указатель, изображение шкалы, которое наблюдает оператор через окуляр I.
Перемещение измерительного стержня 8 вследствие изменения размера изделия 9 вызывает поворот зеркала 6 вокруг оси 7 и соответствующее смещение изображения шкалы относительно неподвижного указателя.
В оптиметре используются принцип оптического рычага и его передаточное отношение
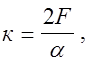
где 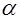 - расстояние от точки опоры зеркала 6 до оси измерительного стержня 8 (малое плечо рычага);
- расстояние от точки опоры зеркала 6 до оси измерительного стержня 8 (малое плечо рычага);
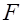 - фокусное расстояние объектива 5 (большое плечо рычага).
- фокусное расстояние объектива 5 (большое плечо рычага).
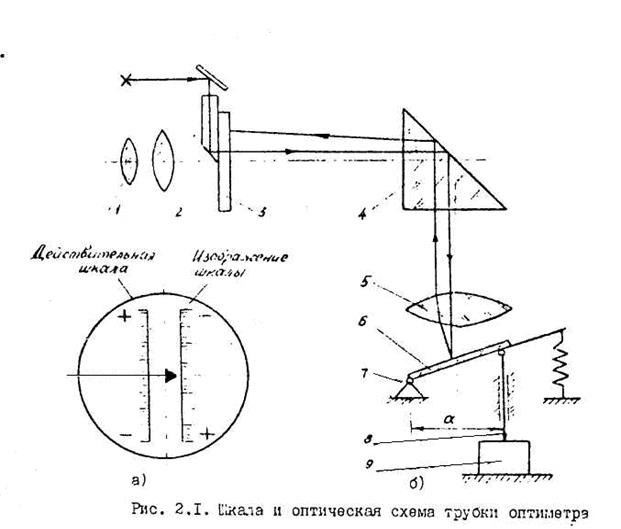
Трубка оптиметра монет быть закреплена в вертикальной или горизонтальной стойке. В первом случае прибор называется вертикальным оптиметром, во втором - горизонтальным.
2.2. Устройство и измерение на вертикальном оптиметре
Вертикальный оптиметр предназначен для измерения наружных размеров точных изделий и калибров относительным методом. Он состоит из трубки оптиметра I (рис. 2.2) и вертикальной стойки, основными частями которой являются: основание 8, плоский стол 4 , колонка 9 и кронштейн 12. Трубка оптиметра крепится в кронштейне винтом 2. Кронштейн перемещается по колонке вращением опорного кольца 10 и закрепляется в требуемом положении винтом II. Арретир 3 служит для поднятия измерительного стержня при установке, снятии изделия и для проверки постоянства показаний прибора.
Измеряемый объект устанавливается на столе 4. Микрометрическая подача стола в вертикальном направлении осуществляется вращением накатной гайки 7. В установленном положении стол крепится винтом 6.
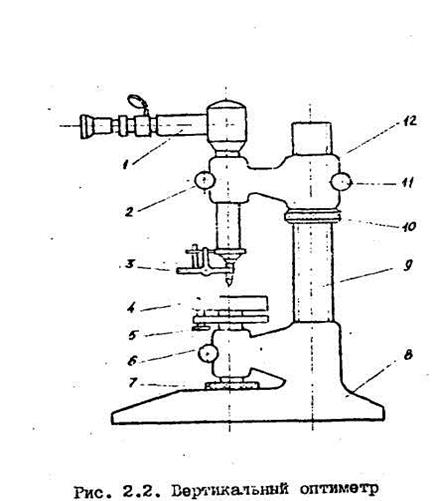
Регулировочные винты и гайки 5 служат для установки рабочей плоскости стола перпендикулярно линии измерения. ПРИ ВЫПОЛНЕНИИ РАБОТЫ ВИНТ 5 НЕ ВРАЩАТЬ, Т. К. УСТАНОВКА СТОЛИКА ПРОИЗВЕДЕНА ЗАPAHEЕ!!!
Метрологическая характеристика вертикального оптиметра: цена деления - 0,001 мм; диапазон показаний по шкале ± 0,1 мм; диапазон измерений прибора – 0 ... 180 мм, предельная погрешность измерения - ± 0,3 мкм.
2.3. Метрологические характеристики измерительных средств
Метрологическими характеристикам средств измерений называет характеристики, оказывающие влияние на результаты и погрешности измерений. Основными характеристиками являются:
ЦЕНА ДЕЛЕНИЯ шкалы - изменение измеряемой величины, соответствующее перемещению указателя на одно деление,
ПРЕДЕЛЫ ИЗМЕРЕНИЙ ПО ШКАЛЕ (диапазон показаний) - область значений измеряемой величины, ограниченной ее начальным и конечным значениями.
ПРЕДЕЛЫ (диапазон) ИЗМЕРЕНИЙ ПРИБОРА - область значений измеряемой величины, для которой нормированы допускаемые погрешности средства измерений, т.е. наибольшее и наименьшее значения, которые может показать данный прибор.
ДОПУСКАЕМОЙ ПОГРЕШНОСТЬЮ измерительного средства называется наибольшая погрешность, при которой измерительное средство может быть допущено к применению. Для наиболее распространенных измерительных средств значения допускаемых погрешностей приведены в таблицах [1] .
2.4. Введение в теорию погрешностей измерения
Измерение, какой либо величина не дает ее истинного значения из-за неизбежных погрешностей измерения.
Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой величины. Анализируя распределения частоты появления погрешностей той или иной величины относительно истинного размера, выделяют два вида составляющих погрешностей измерения: случайные и систематические.
Систематические погрешности постоянны для всей серии измерений или являются некоторыми функциями времени. Причины их появления могут быть обнаружены, изучены и устранены или учтены путем введения поправок.
Появление случайных погрешностей носит случайный характер, а сами погрешности и их распределение могут быть описаны методами математической статистики и теории вероятностей. Случайные погрешности измерения являются результатом взаимодействия большого числа факторов: непостоянство измерительного усилия, зазоры и силы трения в соединениях деталей механизма прибора, погрешности отсчета по шкале, различная точность установки детали на измерительную позицию и т.д. Случайные погрешности проявляются в различных показаниях прибора при многократном измерении одного и того же размера.
Многочисленными экспериментами показано, что при использовании универсальных приборов погрешности измерения изменяются по закону, близкому к закону нормального распределения, поэтому случайные погрешности характеризуется следующими свойствами:
1) равные по абсолютной величине положительные и отрицательные случайные погрешности равновероятны;
2) большие по абсолютной величине погрешности встречаются реже малых погрешностей;
3) среднему значению случайной погрешности отвечает наибольшая вероятность.
Из первого и третьего свойства следует, что наиболее достоверное значение измеряемого размера при многократном измерении есть среднее арифметическое ( 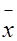 ) из полученных результатов. При количестве измерений n ≤ 25
) из полученных результатов. При количестве измерений n ≤ 25
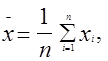 (2.1)
(2.1)
где хi - результаты измерений.
Значение 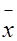 определяет центр группирования значений случайной величины. Алгебраическая сумма отклонений от среднего равна нулю.
определяет центр группирования значений случайной величины. Алгебраическая сумма отклонений от среднего равна нулю.
Практически наиболее важен вопрос о том, насколько велики отклонения случайной величины от ее среднего значения, т.е. каково рассеяние случайной величины. Характеристикой меры рассеяния является средняя квадратическая погрешность.
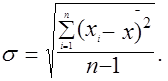 (2.2)
(2.2)
На основании значения σ устанавливается предельная погрешность Δlim средства измерения.
При распределении погрешностей по нормальному закону
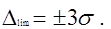 (2.3)
(2.3)
С вероятностью 99,73 % можно утверждать, что в пределах всей шкалы погрешность данного прибора должна бить менее Δlim . Погрешности, выходящие за пределы 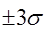 , исключаются из результатов измерений как грубые ошибки.
, исключаются из результатов измерений как грубые ошибки.
Средняя квадратическая и предельная погрешности определяют точность, отдельного измерения данного ряда. Поэтому при однократном измерении универсальными средствами результат записывается следующим образом:
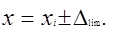 (2.4)
(2.4)
С уменьшением погрешности определенее результат и меньше интервал, в пределах которого может находиться искомый размер.
Для повышения точности измерений при отсутствии средств измерений c меньшей погрешностью производят многократные измерения одного и того же размера. В соответствии с теорией вероятности предельная погрешность Δ’lim среднего арифметического уменьшается.
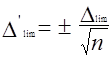 (2.5)
(2.5)
Результат при многократных измерениях записывается следующим образом: 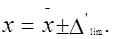 (2.6)
(2.6)
2.5. Определение случайной погрешности прямых измерений
2.5.1. Выполнение измерений
1. Набрать блок концевых мер, размер которого принимается равным номинальному размеру объекта измерения, и притереть его к толу прибора.
2. Провести грубую настройку прибора. Освободив винт II (рис.2.2) и вращая кольцо 10, осторожно опустить кронштейн 12 с трубкой так, чтобы между наконечником и поверхностью блока был просвет 1 ... 2мм. Закрепить винт II.
3. Провести окончательную настройку. Освободив винт 6, вращать гайку 7 микроподачи стола, добиваясь совпадения указателя с нулем шкалы. Закрепить стол винтом 6.
4. Проверить правильность нулевой установки арретированием, нажав 2...3 раза на рычажок 3. Если нулевая установка собьется, настройку следует повторить. После этого, нажав рычажок 3, удалить блок мер и заменить его объектом измерения - калибром-пробкой.
5. Измерить калибр 25 раз в одном и том же сечении, чтобы исключить влияние погрешностей формы, неоднородности поверхностей и т.д. Результаты измерений завести в отчетную карту в виде отклонений от номинального размера (что упрощает обработку ряда результатов измерения).
2.5.2 Обработка результатов измерений
Обработка ряда измерений имеет целью получение наиболее достоверного результата с оценкой его точности. Используя формулы 2.I ... 2.6,определяем основные характеристики рассеивания. При вычислении средней квадратической погрешности результаты следует округлять: при n ≤ 25 сохранять не более двух значащих цифр, а при n > 25 - не более трех. При обнаружении отклонений от среднего ( 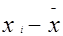 ), превышающих ± 3σ, эти результаты измерения вычеркиваются как имеющие грубые погрешности, и производится новый расчет
), превышающих ± 3σ, эти результаты измерения вычеркиваются как имеющие грубые погрешности, и производится новый расчет 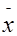 и σ. Результаты математической обработки ряда измерений заносим в таблицу 2.1.
и σ. Результаты математической обработки ряда измерений заносим в таблицу 2.1.
Таблица 2.1
Результаты измерений и их математическая обработка
| № п/п | Результаты отдельных измерений 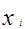 , мкм , мкм | Отклонения от среднего значения ( 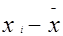 ), мкм ), мкм | Квадрат отклонений ( 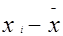 )2 )2 | Данные об объекте измерения |
| 1. 2. 3. . . . 25. | Размер блока мер для настройки | |||
| Средняя квадратическая погрешность ряда измерения σ, мкм | ||||
 Средняя квадратическая погрешность среднего арифметического Средняя квадратическая погрешность среднего арифметического 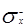 , мкм , мкм | ||||
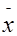 = = | Σ( 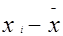 )= )= | Σ( 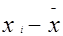 )2= )2= | Предельная погрешность 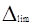 = = 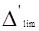 = = | |
| Результаты измерений калибра: |
2.6. Определение погрешности вертикального оптиметра
2.6.1. Выполнение измерений
Для оценки погрешности прибора необходимо измерить объект в одном сечении 25 раз с отсчетом на глаз долей целого деления. После каждого измерения деталь необходимо класть на стол, а не держать в руках, чтобы она не нагревалась от рук и чтобы каждое, измерение было новым. Результаты измерений занести в отчетную карту с учетом знака по шкале прибора.
2.6.2. Обработка измерений
1. По формулам 2.1 , 2.2 , 2.3 рассчитать статистические характеристики.
2. Сравнить полученную предельную погрешность прибора с допустимой по аттестату, и сделать заключение о годности прибора к работе.
2.7. Контрольные вопросы
2.7.1. Объясните оптическую схему и принцип действия оптиметра.
2.7.2. Объясните настройку и приемы измерения на вертикальном оптиметре.
2.7.3. Каковы основные метрологические характеристики оптиметра?
2.7.4. Приведите график закона нормального распределения и объясните основные характеристики и свойства.
2.7.5. Как определяется средняя квадратическая погрешность ряда измерений?
2.7.6. Что характеризует предельная погрешность измерения? Приведите формулу.
2.7.7. Что характеризует предельная погрешность среднего арифметического? Приведите формулу.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Единая система допусков и посадок СЭВ в машиностроении и приборостроении. Контроль деталей: Справочник. - М.: Изд. стандартов, 1987. С. 32 ... 45.
2. Якушев А. И., Воронцов Л. Н., Федотов Н.Н. Взаимозаменяемость, стандартизация и технические измерения: Учебник для вузов. - М.: Машиностроение, 1986. С. 120 ... 122, 130.
3. Лабораторная работа № 7
ИЗМЕРЕНИЕ РАДИАЛЬНОГО И ТОРЦЕВОГО БИЕНИЯ
Цель работы: ознакомление с приемами измерения радиального и торцевого биения, определение их степени точности у измеряемых деталей.
Инструменты и материалы для работы:
прибор для проверки изделий на биение в центрах;
призмы;
индикатор на стойке;
объекты измерения и их чертежи;
протирочные материалы.
3.1. Последовательность выполнения работы
3.1.1. Ознакомиться с базовыми поверхностями у валов.
3.1.2. Ознакомиться с прибором для проверки на биение.
3.1.3. Измерить радиальное и торцевое биение вала в центрах.
3.1.4. Измерить радиальное и торцевое биение вала относительно общей оси.
3.1.5. Измерить радиальное и торцевое биение вала на призме.
3.1.6. Результаты измерения занести в бланк отчета.
Таблица 3.1
Метрологические характеристики прибора
| Измерение торцевого и радиального биения | ||
| Метрологическая характеристика индикатора | Данные о детали | |
| Цена деления | Эскиз детали с указанием размеров | |
| Точность отсчета | ||
| Пределы измерения |
Таблица 3.2
Результаты измерений
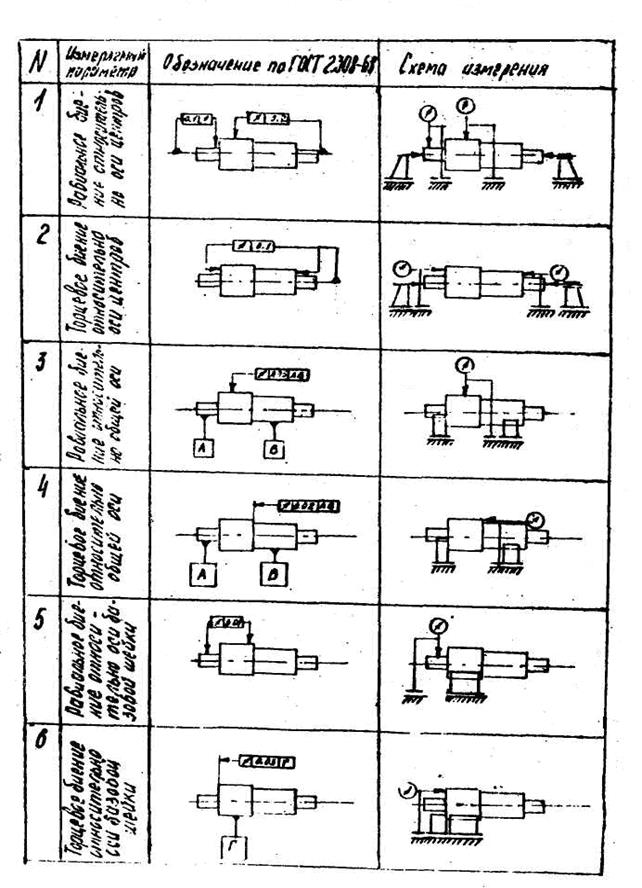
| № п/п | Измеряемый параметр | Схема измерений | Показания индикатора | Действ. отклонения | Степень точности по ГОСТ 24648 - 81 |
Радиальное и торцевое биение у поверхностей валов
Радиальное биение - это разность между наибольшим и наименьшим расстоянием от реальной поверхности до базовой оси вращения детали, перпендикулярной направлению намерения. Радиальное биение является результатом совместного проявления отклонения от круглости профиля рассматриваемого сечения и отклонения его центра относительно базовой оси (соосности).
Торцевое биение - это разность наибольшего и наименьшего расстояния от точек реальной торцевой поверхности, расположенных на окружности заданного диаметра, до плоскости, перпендикулярной к оси вращения детали. Если диаметр не задан, то торцевое биение определяется на наибольшем диаметре торцевой поверхности.
Торцевое биение является результатом совместного проявления отклонения от плоскостности рассматриваемой поверхности отклонения от перпендикулярности ее относительно базовой оси. Погрешности взаимного расположения, в том числе и биение, долгот задаваться конструктором и контролироваться от баз.
База - совокупность поверхностей, линий и точек, по отношению к которым определяется расположение рассматриваемой поверхности.
Измерение биений необходимо проводить относительно тех поверхностей, которыми деталь базируется в механизме.
Базовыми поверхностями у валов могут быть: а) одна цилиндрическая поверхность (таблица 3.3, пункт 5,6), консольный вал; в этом случае биение остальных цилиндрических и торцевых поверхностей долят определяться при установке детали на широкую призму этой базовой поверхностью;
6) две цилиндрические поверхности (таблица 3.3,пункт 3,4), двухопорный вал; в этом случае все пространственные отклонения измеряются относительно общей оси опорных поверхностей, установленных на призме. При этом для контроля биений вал устанавливается на узкие призмы серединами базовых поверхностей.
Для упрощения технологического процесса часто используют вспомогательные технологические базы. Для валов это центровые отверстия. Иногда контроль пространственных отклонений проводят относительно вспомогательных технологических баз. Это наиболее простой, но не всегда точный метод (таблица 3.3, пункт 1,2).
3.2. Прибор для проверки изделий на биение
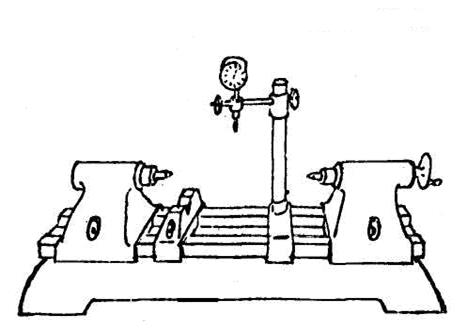
Рис. 3.1. Прибор для контроля биений
На станине 1 установлены две бабки с центрами 2 и 5, которые перемещаются и закрепляются в нужном положении. На той же станине установлена стойка 4 с индикатором 3, при помощи которого производят измерения биений. Кроме бабок с центрами на основание могут устанавливаться различные призмы. При контроле торцевого биения на стойке индикатора закрепляется регулирующий упор.
3.3. Измерение радиального биения в центрах
Установить деталь в центрах и закрепить бабки 2 и 5 в нужном положении винтами.
Для измерения радиального биения:
3.3.1. расположить измерительный наконечник индикатора приблизительно по оси детали над контролируемой шейкой и добиться натяга около 0,5 мм;
3.3.2. медленно вращая деталь в центрах, определить наибольшее и наименьшее показания индикатора, разница между ними дает величину радиального биения. Повторить измерения в различных местах и большее значение занести в таблицу 3.2.
3.3.3. повторить пункты 3.3.1 и 3.3.2 при контроле других шеек.
3.4. Измерение торцевого биения в центрах
3.4.1. Расположить индикатор так, чтобы его измерительный стержень располагался вдоль оси детали и касался измерительным наконечником торца детали на возможно большем расстоянии от оси детали, добиться натяга 0,5 мм.
3.4.2. Медленно вращать деталь, определить наибольшее и наименьшее показания индикатора. Разница между ними даст величину торцевого биения.
3.5. Измерение радиального биения относительно общей оси
Для определения радиального биения всех шеек вала относительно общей оси базовых шеек необходимо установить две призмы на основание так, чтобы они касались шеек приблизительно в средней части, призмы закрепить и повторить пункты 3.3.1, 3.3.2, 3.3.3 раздела измерения радиального биения в центрах.
3.6. Измерение торцевого биения относительно общей оси
Для определения торцевого биения относительно общей оси необходимо установить деталь на призмы базовыми шейками. Повторить пункты 3.4.1 и 3.4.2 раздела измерения торцевого биения в центрах.
3.7. Измерение радиального биения на широкой призме
Для определения радиального биения заданной поверхности относительно базовой необходимо установить широкую призму на основание. Уложить на нее деталь базовой поверхностью. Повторить пункты 3.3.1, 3.3.2, 3.3.3 раздела измерения радиального биения в центрах.
3.8. Измерение торцевого биения на широкой призме
Для определения торцевого биения в широкой призме необходимо деталь установите в призму базовой поверхностью. Повторить пункты 3.4.1 и 3.4.2 раздела измерения радиального биения в центрах.
3.9. Контрольные вопросы
3.9.1. Дайте определение радиального и торцевого биения.
3.9.2. Что такое базовые поверхности? Какие поверхности могут быть базовыми у валов?
3.9.3. Выполнить схемы измерения радиального и торцевого биения: в центрах; относительно общей оси; относительно базовой шейки.
3.9.4. Объясните устройство прибора для измерения биений.
3.9.5. Объясните методику измерения биений: в центрах, на призме.
Таблица 3.3