О процедурах ВЛП-опровержения
Всякое опровержение по определению есть некоторая синтаксическая конструкция. Как находить эти конструкции?
Пространством поиска опровержений является дерево некоторого, определяемого далее, вида. При построении этого дерева для сокращения его размерности правило выбора можно считать наперед фиксиро-
ванным в соответствии с § 6.
Поисковое дерево. ВЛП-дерево для 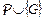 и
и  определяется так:
определяется так:
а) каждая вершина дерева есть цель (возможно, пустая);
б) корневая вершина есть 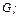
в) пусть 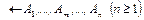 есть вершина в этом дереве, а
есть вершина в этом дереве, а 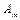 – атом, выбранный посредством
– атом, выбранный посредством 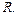 Тогда эта вершина имеет потомка для каждого программного дизъюнкта
Тогда эта вершина имеет потомка для каждого программного дизъюнкта 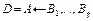 такого, что
такого, что 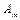 и
и 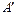 унифицируемы,
унифицируемы, 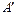 – заголовок подходящего варианта
– заголовок подходящего варианта 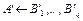 дизъюнкта
дизъюнкта 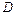 . Это – потомок вида
. Это – потомок вида
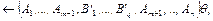
где 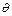 – но-унификатор для
– но-унификатор для 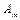 и
и 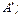
г) вершины, которые являются пустыми дизъюнктами, не имеют потомков.
Каждая ветвь этого дерева есть вывод из 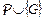 . Те ветви, которые завершаются пустым дизъюнктом, являются ВЛП-опровержениями для
. Те ветви, которые завершаются пустым дизъюнктом, являются ВЛП-опровержениями для 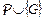 – (успешные ветви). В ВЛП-дереве могут быть бесконечные ветви. Некоторые непустые цели могут не иметь потомков. Это – цели, выбранные атомы которых не унифицируемы с заголовком ни одного программного дизъюнкта. Этим тупиковым целям отвечают и тупиковые ветви, в них ведущие.
– (успешные ветви). В ВЛП-дереве могут быть бесконечные ветви. Некоторые непустые цели могут не иметь потомков. Это – цели, выбранные атомы которых не унифицируемы с заголовком ни одного программного дизъюнкта. Этим тупиковым целям отвечают и тупиковые ветви, в них ведущие.
Если задано ВЛП-дерево, то правилом поиска называется стратегия поискана дереве успешных ветвей. Процедура ВЛП-опровержения определяется своими правилами выбора и поиска.
Способ фиксации правила выбора  влияет на размерность дерева, которое для одного
влияет на размерность дерева, которое для одного  может быть конечным, а для другого
может быть конечным, а для другого  – бесконечным. Тем не менее из следствий 4 и 5 вытекают следующие утверждения.
– бесконечным. Тем не менее из следствий 4 и 5 вытекают следующие утверждения.
Пусть  – любое фиксированное правило выбора.
– любое фиксированное правило выбора.
Следствие 6. Если 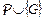 невыполнимо, то ВЛП-дерево для
невыполнимо, то ВЛП-дерево для 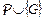 и
и  имеет по крайней мере одну успешную ветвь.
имеет по крайней мере одну успешную ветвь.
Следствие 7. Каждая корректная ответная подстановка 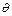 для
для 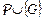 ображается» на ВЛП-дереве для
ображается» на ВЛП-дереве для 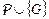 и
и  , т.е. для
, т.е. для 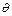 имеется успешная ветвь, которой соответствует
имеется успешная ветвь, которой соответствует  -ответная подстановка, более общая чем
-ответная подстановка, более общая чем 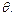
В связи с применением логического программирования в базах данных нас могут интересовать не одна, а все  -ответные подстановки. Поэтому желательно, чтобы правило поиска удовлетворяло такому требованию, что любая успешная ветвь им будет в конечном счёте найдена (требование полноты относительно выводимости).
-ответные подстановки. Поэтому желательно, чтобы правило поиска удовлетворяло такому требованию, что любая успешная ветвь им будет в конечном счёте найдена (требование полноты относительно выводимости).
При поиске на деревьях используются разные стратегии: «вначале вглубь», «вначале вширь» и др. (об этом читайте в монографии [12]).
Если же ВЛП-дерево бесконечно и используется стратегия «вначале вглубь», то такое правило поиска может не удовлетворять выставленному требованию полноты. С другой стороны, стратегия «вначале вширь» иногда оказывается неэффективной из-за сложной комбинаторики.
Само логическое программирование обеспечивает удобные возможности для двух основных видов параллелизма: так называемый И-параллелизм, который возможен, если одновременно могут преследоваться разные подцели
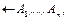
и ИЛИ-параллелизм, который возможен, если в связи с рассматриваемой целью могут в одно и то же время использоваться разные альтернативные правила:
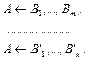
Вместе с тем пока большинство созданных ПРОЛОГ-систем логического программирования (исключая LOGLISP [13] и некоторые другие) используют стратегию «вначале вглубь» и механизм возврата (back-tracking) при попадании в тупиковую вершину. Функционирование таких систем с механизмом возврата – строго последовательное. В них правило поиска сводится к правилу упорядочения, т.е. к правилу, указывающему, в каком порядке должны быть испытаны программные дизъюнкты. Упорядочение дизъюнктов в  и их испытание всегда в соответствии с этим порядком – простое и часто достаточно эффективное правило поиска, хотя и имеет недостаток, состоящий в том, что для каждой цели порядок испытания фактов и правил жёстко фиксирован, т.е. один и тот же.
и их испытание всегда в соответствии с этим порядком – простое и часто достаточно эффективное правило поиска, хотя и имеет недостаток, состоящий в том, что для каждой цели порядок испытания фактов и правил жёстко фиксирован, т.е. один и тот же.
Рассмотрим полноту ПРОЛОГ-систем, в которых используется механизм возврата и фиксированный порядок испытания программных дизъюнктов.
При этом большинство ПРОЛОГ-систем (см., например, [14]) используют правило выбора 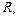 которое всегда выбирает первый (слева) атом цели. Однако имеются системы и с более сложными правилами
которое всегда выбирает первый (слева) атом цели. Однако имеются системы и с более сложными правилами  , например IC-PROLOG [15], MU-PROLOG [16] и др. По следствию 6, если
, например IC-PROLOG [15], MU-PROLOG [16] и др. По следствию 6, если 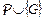 невыполнимо, независимо от
невыполнимо, независимо от  соответствующее ВЛП-дерево всегда содержит успешную ветвь. Тем не менее система с механизмом возврата, фиксированным порядком испытания программных дизъюнктов и произвольным
соответствующее ВЛП-дерево всегда содержит успешную ветвь. Тем не менее система с механизмом возврата, фиксированным порядком испытания программных дизъюнктов и произвольным  не гарантирует отыскания успешной ветви. Это – плата за отказ, например, от полной стратегии поиска «вначале вширь» (которую более обоснованно использовать в базах данных).
не гарантирует отыскания успешной ветви. Это – плата за отказ, например, от полной стратегии поиска «вначале вширь» (которую более обоснованно использовать в базах данных).
Рассмотрим примеры.
Пример 17. Пусть  и
и 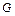 из примера 1 (см. также обозначения примера 13). Выбрав в качестве
из примера 1 (см. также обозначения примера 13). Выбрав в качестве  правило, упомянутое выше, а в качестве порядка на
правило, упомянутое выше, а в качестве порядка на  порядок ((4), (5), (6)), получим дерево просмотра целей
порядок ((4), (5), (6)), получим дерево просмотра целей
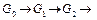 □.
□.
Поменяв порядок на ((5), (4), (6)), при том же  получим дерево
получим дерево
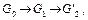
где 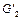 – тупиковая вершина. Возвращаясь к цели
– тупиковая вершина. Возвращаясь к цели 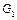 и используя следующий, ещё не испытанный, дизъюнкт в
и используя следующий, ещё не испытанный, дизъюнкт в  , т.е. факт (4), получим
, т.е. факт (4), получим 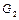 и далее □. В целом, дерево просмотра целей примет вид, представленный на рис. 3.
и далее □. В целом, дерево просмотра целей примет вид, представленный на рис. 3.
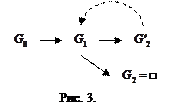
Если в качестве  для той же программы
для той же программы  и цели
и цели 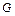 примем правило выбора самого последнего (слева) атома цели, то при любом порядке на
примем правило выбора самого последнего (слева) атома цели, то при любом порядке на  получается дерево
получается дерево
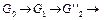 □,
□,
где 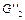 есть цель
есть цель 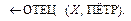
Пример 18. Пусть  – программа вида:
– программа вида:
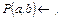 (11)
(11)
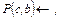 (12)
(12)
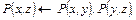 (13)
(13)
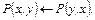 (14)
(14)
а 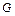 – цель
– цель 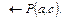 Используя произвольный, но фиксированный порядок в
Используя произвольный, но фиксированный порядок в  и любое правило выбора
и любое правило выбора 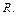 система с механизмом возврата (и стратегией «вначале вглубь») никогда не найдет опровержения. Действительно, дизъюнкты (13) и (14) имеют заголовки, не содержащие констант и функциональных символов. Поэтому их заголовки унифицируемы с любой (непустой) целью, которая может возникнуть. Если дизъюнкт (13) предшествует по порядку испытаний дизъюнкту (14), то система никогда не дойдет до дизъюнкта (14) (и наоборот). Однако все дизъюнкты (11)–(14), как нетрудно проверить, необходимы для опровержения.
система с механизмом возврата (и стратегией «вначале вглубь») никогда не найдет опровержения. Действительно, дизъюнкты (13) и (14) имеют заголовки, не содержащие констант и функциональных символов. Поэтому их заголовки унифицируемы с любой (непустой) целью, которая может возникнуть. Если дизъюнкт (13) предшествует по порядку испытаний дизъюнкту (14), то система никогда не дойдет до дизъюнкта (14) (и наоборот). Однако все дизъюнкты (11)–(14), как нетрудно проверить, необходимы для опровержения.
Пример 19 (более полный пример и его модификации см. в [14]). Рассмотрим задачу выбора механика для включения его в состав формируемой экспедиции. Программа  содержит набор фактов, устанавливающих специальности предполагаемых участников экспедиции и состояние их здоровья, а также правило включения в экспедицию:
содержит набор фактов, устанавливающих специальности предполагаемых участников экспедиции и состояние их здоровья, а также правило включения в экспедицию:
КТО-ЕСТЬ-КТО (БОТАНИК, ВАСЯН) 
КТО-ЕСТЬ-КТО (СИНОПТИК, ФЕДЯКОВ) 
КТО-ЕСТЬ-КТО (МЕХАНИК, КАЛЯЕВ) 
КТО-ЕСТЬ-КТО (МЕХАНИК, САЖИН) 
ЗДОРОВ (ВАСЯН) 
ЗДОРОВ (ФЕДЯКОВ) 
ЗДОРОВ (САЖИН) 
ВКЛЮЧИТЬ (СПЕЦИАЛЬНОСТЬ, ФАМИЛИЯ) 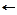 КТО-ЕСТЬ-КТО (СПЕЦИАЛЬНОСТЬ, ФАМИЛИЯ), ЗДОРОВ (ФАМИЛИЯ)
КТО-ЕСТЬ-КТО (СПЕЦИАЛЬНОСТЬ, ФАМИЛИЯ), ЗДОРОВ (ФАМИЛИЯ)
(«специальность» и «фамилия» объявляются переменными).
В качестве цели решения задачи выберем цель 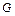 вида
вида
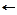 ВКЛЮЧИТЬ (МЕХАНИК, ФАМИЛИЯ).
ВКЛЮЧИТЬ (МЕХАНИК, ФАМИЛИЯ).
Считая программу упорядоченной так, как она записана, правилом выбора  – выбор первого (слева) атома и используя возврат, получим дерево просмотра целей, представленное на рис. 4.
– выбор первого (слева) атома и используя возврат, получим дерево просмотра целей, представленное на рис. 4.
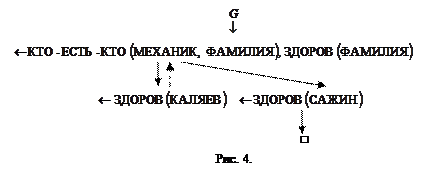
При этом на успешной ветви образуются
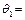 {ФАМИЛИЯ / X, МЕХАНИК / СПЕЦИАЛЬНОСТЬ},
{ФАМИЛИЯ / X, МЕХАНИК / СПЕЦИАЛЬНОСТЬ},
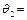 {САЖИН / ФАМИЛИЯ},
{САЖИН / ФАМИЛИЯ},
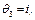
где 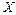 – переменная из подстановки, образующей подходящий вариант дизъюнкта (15). Композиция подстановок
– переменная из подстановки, образующей подходящий вариант дизъюнкта (15). Композиция подстановок 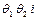 имеет вид {САЖИН / X, МЕХАНИК /СПЕЦИАЛЬНОСТЬ, САЖИН / ФАМИЛИЯ}.
имеет вид {САЖИН / X, МЕХАНИК /СПЕЦИАЛЬНОСТЬ, САЖИН / ФАМИЛИЯ}.  -ответной подстановкой явится подстановка {САЖИН /ФАМИЛИЯ}.
-ответной подстановкой явится подстановка {САЖИН /ФАМИЛИЯ}.
Упражнения:
22. Приведите пример программы и цели, для которых ВЛП-дерево конечно в случае одного правила выбора и бесконечно при другом.
23. Приведите пример, раскрывающий существенность требования предварительного преобразования программного дизъюнкта в подходящий вариант при построении потомков в поисковом дереве.
24. Чем отличается поисковое дерево от дерева просмотра целей (см. примеры 17 и 19)?
25. Проверить, что всякое опровержение для множества 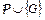 из примера 18 использует каждый из четырёх дизъюнктов программы.
из примера 18 использует каждый из четырёх дизъюнктов программы.
26. Для выработки навыков формализации и освоения изложенного материала поупражняйтесь в составлении логических программ и решении Ваших задач.
Заключение
Основной тезис логического программирования утверждает, алгоритмизация решения задач состоит в указании двух компонент: «логики» и «управления». Логика определяет, ЧТО за задача должна быть решена. Управление определяет, КАК она должна быть решена. Идеалом логического программирования является то, чтобы программист (пользователь) указывал бы (специфицировал)только логическую компоненту задачи. Управление должно осуществляться исключительно системой логического программирования (обычно некоторым интерпретатором).
Однако этот идеал, как мы видели в § 7, ещё не достигнут.
Достижение идеала логического программирования предполагает решение двух основных проблем. Первая из них – это проблема управления. В настоящее время программистам приходится указывать разную управляющую информацию частично упорядочением дизъюнктов и атомов в дизъюнктах, а частично введением в дизъюнкты как бы на правах атомов таких нелогических управляющих признаков, как признак отсечения (который подавляет повторный просмотр поддеревьев, нежелательный в некоторых случаях). Однако эти управляющие признаки недостаточно удовлетворительны по ряду причин [8]. Первой задачей в решении проблемы управления является предоставление программистам более удовлетворительных управляющих средств. Второй задачей является передача ответственности за управление от программиста самой системе.
Вторая проблема логического программирования – это проблема работы с отрицаниями. Хорновские дизъюнкты не имеют достаточной выразительной силы, и поэтому для вывода негативной информации применяются дополнительные специальные правила, например правило неуспеха [17]. В логические программы, а именно в тела дизъюнктов, вводят отрицания атомов (на практике многие программы более естественно записываются именно так). Продолжаются исследования по разработке таких программ и в целом по реализации отрицания в системах логического программирования.
Ряд практических задач сводится к проверке выполнимости логических формул (т.е. существованию модели [2, 3]). Соответствующий подход реализован в системах логического программирования CLP (Constraint Logic Programming). Задача с неполной информацией или с ограниченными ресурсами, в том числе задачи диагностики, объяснения наблюдений, автоматизации построения теорий, нуждаются в третьем подходе к логическому программированию – абдуктивном подходе, в рамках которого могут отыскиваться недостающие условия и конструктивные средства для разрешения поставленной задачи.
Исчисление позитивно-образованных формул [19] в сравнении с методом резолюций обладает рядом преимуществ (более выразительный язык, меньшая комбинаторность поиска выводов, совместимость с эвристиками предметной области, модифицируемость семантики и др.). Является актуальным использование этой теоретической базы для создания более эффективных практических систем логического программирования во всех указанных выше классах задач.
Использованная литература
1. Глушков В.М. Кибернетика // Математическая энциклопедия. Т. 2. С. 850–855. М.: Советская энциклопедия, 1979.
2. Ершов Ю.Л., Палютин Е.А. Математическая логика. М.: Наука, 1979.
3. Мендельсон Э. Введение в математическую логику. М.: Мир, 1971.
4. Робинсон Дж. Машинно-ориентированная логика, основанная на принципе резолюции // Киберн. сб. Нов. сер. М.: Мир, 1970. Вып. 7. С. 194–218.
5. Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. М.: Наука, 1983.
6. Мальцев А.И. Алгебраические системы. М.: Наука, 1970.
7. Emden M., Kowalski R. The Semantics of Predicate Logic as a Programming Language // JACM. 23. 4. P. 733–742.
8. Lloyd J. Foundation of Logic Programming // Tech. Report. 82/7. Univ. Melbourne, 1983.
9. Apt K., Emden M. Contributions to the Theory of Logic Programming // JACM. 29. 3. P. 841–862.
10. Clark K. Predicate Logic as a Computational Formalism // Res. Report. 79/59. Imper. College, 1980.
11. Hill R. LUSH-Resolution and its Completeness // DGL Memo 78. Univ. Edinburgh, 1974.
12. Уинстон П. Искусственный интеллект. М.: Мир, 1960.
13. Robinson J., Sibert E. Logic Programming in LISP / School of Computer and Information Science. Syracuse Univ., 1980.
14. Система «ПРОЛОГ-ЕС» Введение в ПРОЛОГ (инструкция для пользователя). Киев: ИК АН УССР, 1979.
15. Clark K., McCabe F. The Control Facilities of IC-PROLOG, in Expert Systems in the Micro Electronic Age. Edinburg Univ. Press. P. 122–149.
16. Hayes P. Computation and Deduction // Proc. MFCS Conf., Czechoslovakian Acad. Sci., 1973.
17. Clark K. Negation as Failure, in Logic and Data-bases // Plenum Press. N.Y.,1978. P. 293–322.
18. Fifth Generation Computer Systems // Proc. Internat. Conf. on Fifth Generation Computer Systems / T. Moto-Oka ed. North-Holland Publ. Comp. Amsterdam; N.Y.; Oxford, 1982.
19. Васильев С.Н., Жерлов А.Л., Федосов Е.А., Федунов Б.Е. Интеллектное управление динамически-
ми системами. М.: Наука, ФИЗМАТЛИТ, 2000.
20. Клоксин У., Мелиш К. Программирование на языке Пролог. М.: Мир, 1987 (F.W. Clocksin, C.S. Mellish. Programming in Prolog. Springer-Verlag, 1981).
21. Братко И. Программирование на языке Пролог для искусственного интеллекта. М.: Мир, 1990 (I. Bratko. Prolog Programming for Artificial Intelligence. Addison-Wesley Publ. Comp. Inc. , Wokingham, 1986).
22. Непейвода Н.Н. Прикладная логика. Уч. пос. 2-е изд., исп. и доп. Новосибирск: Изд-во Новосиб. ун-та, 2000.
23. Kakas A.C., Kowalski R.A., Toni F. The Role of Abduction in Logic Programming . Handbook of Logic in Artificial Intelligence and Logic Programming / Eds. D.M. Gabbay, C.J. Hoger, J.A. Robinson. Oxford Univ. Press, 1998.
24. Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фомина М.В. Достоверный и правдоподобный вывод в интеллектуальных системах / Под ред. В.Н. Вагина, Д.А. Поспелова. М.: ФИЗМАТЛИТ, 2004.
25. Вагин В.Н., Хотимчук К.Ю. Методы абдуктивного вывода в задачах планирования работы в сложных объектах // Изв. РАН. Теория и системы управления. 2010. № 5. С. 95–113.
26. Автоматическое порождение гипотез в интеллектуальных системах / Сост. Е.С. Панкратова, В.К. Финн; под ред. В.К. Финна. М.: Книжный дом «ЛИБРОКОМ», 2009.
27. Cox P.T., Pietrzykowski T. General Diagnosis by Abductive Inference // Proc. of the IEEE Symposium on Logic Programming. 1987. P. 183–189.
28. Matyasiki P., Nalepai G.J., Zieciki P. Prolog-Based Real-Time Intelligent Control of the Hexor Mobile Robot // http: // ai. ia. agh. edu. pl / wiki/_media / hekate: bib:ptm-ki 2007.pdf
