Закон исключенного третьего 5 страница

С помощью алгебры логики (математической) можно описывать рассуждения и «вычислять» их результаты, если символам переменных поставить в соответствие некоторые утверждения, называемые высказываниями.

Такое применение алгебры логики получило название логики высказываний. Впоследствии оно было расширено добавлением переменных, принимающих значения из множества понятий, что сформировало логику предикатов.

Дальнейшее развитие логики высказываний основано на допущении нескольких значений истинности (например, кроме значений «истина» и «ложь» допускается третье значение − «неопределенность»). В подобных случаях используют аппарат многозначной логики. Если истинность предложений определяется с некоторой вероятностью, то логика высказываний превращается в вероятностную логику.

Понятие закона исключения третьего позволяет полностью использовать в логике высказываний аппарат двузначной логики (рассмотренный в разделе 3). В данном разделе дисциплины рассматривается только двузначная логика высказываний и логика предикатов.

План раздела состоит в том, чтобы на основе предварительного рассмотрения основных понятий логики высказываний и логики предикатов ввести понятие «формальной теории» и наиболее часто используемых исчислений: исчисления высказываний и исчисления предикатов.

Понимание основ теории доказательств, которая рассматривается в данном разделе, необходима для логического построения передовых компьютерных технологий.

Введем специфическую «логическую» терминологию и укажем её связь с положениями раздела «Элементы математической логики. Алгебра булевых функций».

Определение.

Высказывание – это утверждение или повествовательное предложение, о котором можно сказать, истинно оно или ложно, но ни то и другое одновременно.

В логике высказываний рассматривают не содержание и даже не структуру высказывания, а ограничиваются только тем его свойством, что оно представляет собой истину или ложь.

Пример.

Предложения, являющиеся высказываниями:

а) Два умножить на два равно четыре ( ).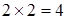

б) Рим − столица Франции.

Предложения, не являющиеся высказываниями:

а) Кто Вы? (вопрос).

б) Прочтите эту книгу до следующего занятия (приказ или восклицание).

в) Это утверждение ложно (внутренне противоречивое утверждение).

Определение.

Высказывания, которые соответствуют простым повествовательным предложениям, т.е. не имеют составных частей, называются атомами (элементарными высказываниями, атомарными формулами).

Высказывание можно рассматривать как величину, (пропозициональную переменную, высказывательную переменную), которая может принимать два значения: «истина» и «ложь», т.е. принимать истинностное значение.

Определение.

Под истинностным значением понимается абстрактный объект («истина» или «ложь»), сопоставляемый высказыванию в зависимости от того, является это высказывание истинным или ложным. Обозначается: «истина» − И, Т (True) или 1, „ложь” – Л, F (False) или 0.

Определение.

Множество {И, Л} называется множеством истинностных значений.

Пример.

Высказывание « 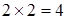» имеет истинностное значение 1 (И).

Высказывание «Рим − столица Франции» имеет истинностное значение 0 (Л).

Можно рассматривать две группы высказываний:

- высказывания, истинностное значение которых независимо от ситуации можно считать однозначно определенным;

- высказывания, зависящие от обстоятельств, которыми руководствуются при его истолковании, и, следовательно, могут принимать различные значения.

Обычно эти обстоятельства не фигурируют явно в простом высказывании.

Пример.

а) Высказывание « 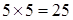» определено однозначно.

б) Истинность таких высказываний, как «Хорошая погода», «Сегодня 31 декабря», «Результат измерений диаметра цилиндра равен 52 мм» зависит, соответственно, от вкусов или критерия оценки погоды, сегодняшней даты, требуемой точности измерения. Высказывание «Завтра будет дождь» может получить значение «истина» или «ложь» в зависимости от конкретной ситуации.

качестве символов для обозначения атомов используются заглавные буквы латинского алфавита 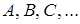или заглавные буквы с индексами. Каждая буква в рассуждении должна обозначать одно и только одно элементарное высказывание.

Пример.

а) - «Снег белый».

б) 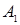- «Аня является студенткой университета».

в) − «Группа КН-13-1 насчитывает 25 студентов».

10.2 Логические связки и формулы логики высказываний

Рассматривая конструкции естественного языка, видим, что простые предложения объединяются в сложные при помощи соответствующих сентенциональных связок (союзов), т.е. сложные предложения состоят из простых предложений и служебных слов («если», «то», «и», «или» и т.п.).

Пример.

Составные (сложные) высказывания:

а) «Снег белый, и температура ниже нуля».

б) «Если Петр на занятиях, то Аня дома».

в) «Петр − студент института или шахтер».

Простые предложения и союзы можно использовать как элементы словаря, необходимого для формализации естественного языка с помощью логики высказываний. Операции логики высказываний – логические связки – рассматриваются как формальные обозначения соответствующих им связок естественного языка. Сентенциональные связки в разговорном языке допускают различные варианты. Поэтому при записи сложного предложения в виде формулы алгебры высказываний важно выяснить характер логической связи между предложениями, не вдаваясь в смысл этих предложений.

Из одних высказываний различными способами можно строить новые, более сложные высказывания, называемые формулами или молекулами, используя те же операции (и их символы), что и в булевой алгебре. Примеры связок и их символов приведены в табл. 10.1.

Таблица 10.1 − Логические связки в логике высказываний

Название	Обозначение	Аналоги естественного языка
Отрицание		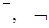не, «неверно, что»
Конъюнкция		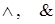и
Дизъюнкция		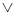или, «или одно из двух …, или оба», либо
Импликация		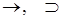влечет, «если, …то», «только если», «только тогда, когда», «есть достаточное условие», «при условии, что», «есть необходимое условие»
Эквивалентность		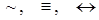эквивалентно, равносильно, «тогда и только тогда, когда», «если и только если», «есть необходимое и достаточное условие»

Рассмотрим примеры и выражения естественного языка, которые соответствуют логическим связкам.

Определение.

Отрицанием высказывания называется высказывание (обозначение 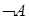), которое истинно тогда и только тогда, когда ложно.

Данная унарная операция соответствует отрицанию в естественном языке, которое может иметь различные синтаксические выражения (см. таблицу 4.1).

Пример.

Пусть имеем высказывание − «Владимир получил электронное письмо от Александра». Отрицанием высказывания является: 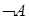− «Владимир не получил электронное письмо от Александра». Данное высказывание можно представить следующим образом: 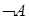− «Неверно, что Владимир получил электронное письмо от Александра».

Определение.

Высказывание 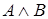, называемое конъюнкцией и , истинно тогда и только тогда, когда истинны оба высказывания и .

Эта логическая операция соответствует в естественном языке связке «и», соединяющей два предложения.

Пример.

Пусть имеем простые высказывания: − «Харьков является первой столицей Украины»; − «Харьков − красивый город».

Составное высказывание, определяющее конъюнкцию, будет иметь вид: 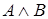− «Харьков является первой столицей Украины и Харьков − красивый город».

Определение.

Высказывание 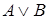, называемое дизъюнкцией и , ложно тогда и только тогда, когда ложны оба высказывания и .

Эта логическая операция соответствует соединению высказываний естественного языка с помощью связки «или», употребляемой в смысле «не исключающее или»: «верно» , или верно , или оба высказывания равны.

Пример.Пусть имеем два атома: − « 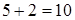» и − « 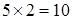». Тогда высказывание « 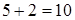или 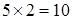» будет соответствовать формуле .

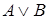Определение.

Высказывание 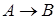, называемое импликацией (условным предложением), ложно тогда и только тогда, когда истинно, а ложно.

В импликации 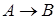высказывание называется посылкой (условием, антецедентом), а - следствием (заключением, консеквентом). Выражаемая импликацией причинно-следственная связь между и на естественном языке описывается следующими оборотами: « влечет », «если , то », « является достаточным основанием для », « , потому что », « при условии выполнения ». Используемые в точных науках понятия достаточного и необходимого условий можно формально выразить с помощью импликации.

Пример.

Пусть имеем два атома: − « − простое» и − « − нечетное». Тогда высказывание «Для того, чтобы было нечетным, достаточно, чтобы было простым» будет соответствовать формуле .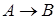

Определение.

Если и - высказывания, то высказывание 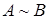, называемое эквиваленцией, истинно тогда и только тогда, когда и либо оба истинны, либо оба ложны.

Эта операция в естественном языке соответствует оборотам: «… тогда и только тогда, когда …», «для того чтобы …, необходимо и достаточно …»,

Пример.

Пусть имеем два атома: − «идет дождь» и − «на небе тучи». Тогда высказывание «Дождь идет тогда и только тогда, когда на небе тучи» будет соответствовать формуле .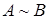

Алфавит логики высказываний содержит следующие символы:

1) высказывательные переменные 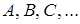или заглавные буквы с индексами;

2) логические символы (связки) ;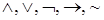

3) символы скобок ( ) и запятую.

Связки могут быть бинарными и унарными. Операции 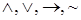являются бинарными логическими связками, операция 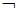− унарной логической связкой.

При записи формул можно обойтись без некоторых скобок, если приписать ранги логическим связкам. Ранги логических связок чаще всего задаются в таком порядке (от высшего к низшему): .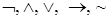

Пример. − «Влажность большая»; − «Температура высокая»; 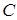− «Мы чувствуем себя хорошо».

Высказывание «Если влажность большая и температура высокая, то мы не чувствуем себя хорошо» можно записать в виде формулы 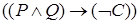или с учетом рангов операций .

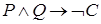Определение.В логике высказываний правильно построенная формула определяется рекурсивно следующим образом:

1. Атом есть формула.

2. Если и - формулы, то - также формулы.

3. Никаких формул, кроме порожденных указанными выше правилами, не существует.

10.3 Алгебра логики и логика высказываний

Определение.

Логика высказываний – это алгебраическая структура 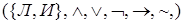) с носителем – двоичным множеством { : «Ложь», : «Истина»}, операциями (логическими связками): « » – конъюнкция, « 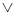» – дизъюнкция, « 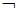» – отрицание, « 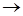» – импликация, «~» – эквивалентность.

Если рассмотреть две алгебры: алгебру логики 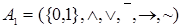и алгебру логики высказываний 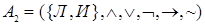, то они будут изоморфны друг другу, так как можно поставить взаимно однозначное соответствие между множествами 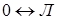, , 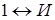а операции просто одинаковы. Если алгебры изоморфны, то элементы и операции можно переименовать так, что совпадает с 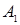. Из условия изоморфности следует, что любое эквивалентное соответствие в алгебре 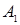сохраняется в 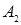. То есть соотношения, полученные в алгебре 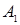, автоматически распространяются на алгебру .

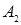С логической точки зрения двоичные объекты, которые рассматривались в разделе «Элементы математической логики. Алгебра булевых функций», - это высказывания, которые могут быть истинными или ложными. Формулы - это составные высказывания, истинность которых определяется истинностью входящих в них элементарных высказываний (обозначаемых буквами) и логическими операциями над высказываниями.

Поэтому все утверждения относительно алгебры логики справедливы и для алгебры логики высказываний.

Если рассматривать формулы, содержащие только логические операции 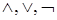, то в логике высказываний выполняется закон двойственности. Кроме того, формулы логики высказываний можно представить в виде ДНФ и КНФ, СДНФ и СКНФ (учитывая изоморфизм алгебр).

10.4 Интерпретация формул логики высказываний. Правильные рассуждения

Определение.

Приписывание истинностных значений атомам, из которых построено высказывание, называется интерпретацией высказывания.

Для высказывания, содержащего атомов, можно составить 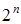интерпретаций, так же, как и для -местной булевой функции.

Формулы логики высказываний можно задавать таблицами истинности, подобно булевым функциям.

Пример.

Рассмотрим таблицу истинности для логических связок логики высказываний (таблица 10.2)

Таблица 10.2 - Таблица истинности логических связок

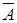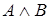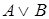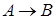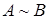Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	И	Л
И	Л	Л	Л	И	Л	Л
И	И	Л	И	И	И	И

Исходя из принимаемых формулами логики высказываний истинностных значений, формулы разделяются на тождественно истинные, тождественно ложные и необщезначимые.

Определение.

Формула называется тождественно истинной (тавтологиейили общезначимой),если она принимает значение «истина» на всех интерпретациях (наборах значений переменных).

Определение.

Формула называется тождественно ложной (противоречивой или невыполнимой),если она принимает значение «ложь» на всех интерпретациях.

Определение.

Формула называется необщезначимойилинепротиворечивой, если она на одних интерпретациях принимает значение «истина», а на других – «ложь».

Определение.

Все формулы, не относящиеся к противоречивым, образуют множество выполнимыхформул.

Пример.

Формула 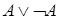− тавтология; формула 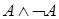является противоречивой; формула 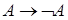является выполнимой.

Перечислим наиболее важные тавтологии, предполагая, что 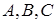− произвольные формулы:

1. ;

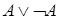2. ;

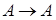3. ;

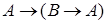4. ;

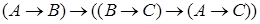5. ;

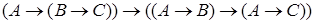6. ;

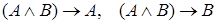7. ;

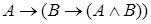8. ;

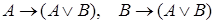9. ;

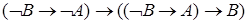10. 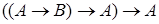(закон Пирса).

При доказательстве утверждений различных математических теорий обычно используют рассуждения, которые на языке логики можно выразить формулами.

Определение.

Рассуждение называется правильным, если оно выражается тождественно истинной формулой.

Таким образом, проверить правильность рассуждения можно, построив соответствующую ему формулу и определив, является ли она тождественно истинной.

Доказать, что формула является тавтологией, можно следующими способами:

1. Построить таблицу истинности этой формулы. Если в таблице истинности на всех интерпретациях функция принимает значение «истина», то соответствующее формуле рассуждение является тавтологией.

2. Применив тождественные преобразования, привести её к виду одного из логических законов. Если в результате преобразований получим значение «истина», то формула является тавтологией.

10.5 Логическая эквивалентность и логическое следствие

Определение.

Две формулы называются равносильными, если на всех наборах значений входящих в них переменных эти формулы принимают одинаковые значения.

Равносильность формул логики высказываний вытекает из тождественности соответствующих формул алгебры логики. Равносильности формул и будем обозначать через 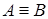. Легко видеть, что равносильность − это отношение эквивалентности (оно рефлексивно, симметрично и транзитивно), поэтому равносильность называют также логической эквивалентностью.