Тема 4.3 Формы логических функций. Функционально-полные системы

Первый вопрос: формы логических функций

ПФ (переключ. Функции) могут быть выражены различными логическими формулами, благодаря возможности проведения над ними эквивалентных преобразований.

(фото)

На практике наиболее удобными для представления ПФ оказываются дизъюнктивные и конъюнктивные формы. Эти формы представляют собой дизъюнкции элементарных конъюнкций или конъюнкции элементарных дизъюнкций.

Конъюнкция (дизъюнкция) любого числа двоичных переменных А, В, С и т.д. является элементарной, если сомножителями (слагаемыми) в ней являются либо одиночные аргументы, либо отрицания одиночных аргументов.

Ранг элементарной конъюнкции (дизъюнкции) определяется числом переменных, входящих в эту конъюнкцию (дизъюнкцию).

Дизъюнктивной нормальной формой (ДНФ ПФ) называется дизъюнкция любого числа элементарных конъюнкций. (примеры на фото).

Совершенной ДНФ (СДНФ ПФ), имеющей n аргументов, называется такая форма, в которой все конъюнкции имеют ранг n. (пример на фото выше).

Конъюнктивной нормальной формой (КНФ ПФ) называется конъюнкция элементарных дизъюнкций. (пример)

Совершенной КНФ (СКНФ ПФ), имеющей n аргументов, называется такая форма, в которой все дизъюнкции имеют ранг n.(пример).

Конъюнктивные формы представления ПФ используются реже чем дизъюнктивные.

Чаще всего ПФ задается словесно, в виде таблицы истинности, алгебраическим выражением. По словесному описанию составляется таблица истинности, а затем записывается СДНФ ПФ.

СДНФ ПФ записывается по таблице истинности в следующей последовательности:

1. Из таблицы истинности выделяются строки, в которых функция принимает значение единицы.

2. Записываются составляющие формулы в виде конъюнкции переменных или их отрицания. Если переменная в данном наборе =1, то она входит в формулу, как не отрицаемая.

3. Конъюнкции объединяют знаком дизъюнкции.

Задача:

Записать ПФ устройство, функционирующее по следующему правилу:

Сигнал на выходе схемы =1, если хотя бы на 2х входах из 3х отсутствует уровень логической единицы.

Таблица истинности:

x	y	z	F

F = + +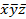

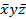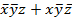
Этапы построения (синтеза) логической схемы

Синтез – это проектирование схемы, реализующей заданный закон её функционирования.

Последовательность этапов синтеза логических схем:

1. Составить таблицу истинности по словесному описанию закона её функционирования;

2. Записать СДНФ ПФ логической схемой;

3. Минимизировать ПФ (упростить);

4. Построить на логических элементах логическую схему, реализующую.