Закон исключенного третьего 4 страница
д) линейные функции.
Определение.
Булева функция 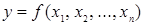 называется функцией, сохраняющей 0, если на нулевой наборе она равна 0, т.е.
называется функцией, сохраняющей 0, если на нулевой наборе она равна 0, т.е.  .
.
Так как на одном из  наборов
наборов  значения таких функций фиксированы, то их число равно
значения таких функций фиксированы, то их число равно  , то есть половина всех функций
, то есть половина всех функций  переменных сохраняет константу 0.
переменных сохраняет константу 0.
Обозначим через 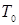 класс функций, сохраняющих 0.
класс функций, сохраняющих 0.
Определение.
Булева функция 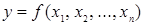 называется функцией, сохраняющей 1, если на единичном наборе она равна 1, т.е.
называется функцией, сохраняющей 1, если на единичном наборе она равна 1, т.е.  .
.
Их число, как и в предыдущем случае, равно половине общего числа всех функций  переменных. Обозначим через
переменных. Обозначим через 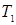 класс функций, сохраняющих 1.
класс функций, сохраняющих 1.
Пример.
Функции  и
и  сохраняют 0 и сохраняют 1, так как
сохраняют 0 и сохраняют 1, так как  ,
,  и
и  ,
,  . Функция
. Функция  не сохраняет 0 и не сохраняет 1, так как
не сохраняет 0 и не сохраняет 1, так как  и
и  .
.
Самодвойственная функция (см. раздел «Принцип двойственности») полностью определяется заданием её значений на половине всех наборов (остальные значения определяются по условию антисимметричности), поэтому число независимых наборов равно  и число всех таких функций
и число всех таких функций  . Обозначим через
. Обозначим через  класс самодвойственных функций.
класс самодвойственных функций.
Рассмотрим важный класс булевых функций - монотонные булевы функции. Обозначим через  класс монотонных функций.
класс монотонных функций.
Зададим два любых набора булевых констант (две интерпретации) в виде  и
и  , на которых введем отношение частичного порядка
, на которых введем отношение частичного порядка 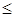 (отношение предшествования).
(отношение предшествования).
Определение.
Для двух наборов 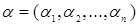 и
и  выполняется отношение предшествования, если
выполняется отношение предшествования, если  .
.
Если хотя бы для одной пары  , где
, где  , отношение
, отношение  не выполняется, то соответствующие им наборы
не выполняется, то соответствующие им наборы  и
и  в отношении порядка не участвуют, т.е. являются несравнимыми.
в отношении порядка не участвуют, т.е. являются несравнимыми.
Пример.Два набора  и
и  находятся в отношении предшествования, т.к.
находятся в отношении предшествования, т.к.  , (
, (  ).
).
Наборы же (0, 1) и (1, 0) не находятся в отношении предшествования.
Определение.
Функция 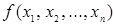 называется монотонной, если для любых двух наборов
называется монотонной, если для любых двух наборов 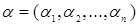 и
и 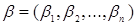 , находящихся в отношении предшествования, имеет место и неравенство
, находящихся в отношении предшествования, имеет место и неравенство 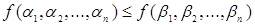 .
.
Функция, эквивалентная монотонной, является также монотонной. Для проверки функции на монотонность необходимо исследовать выполнение неравенства 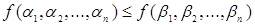 для всех пар наборов
для всех пар наборов  .
.
Пример.Константы 0 и 1 и функция  монотонны. Отрицание
монотонны. Отрицание  немонотонно. Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.
немонотонно. Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.
Пример.
Проведем анализ на монотонность двух функций от трех переменных, заданных таблицей истинности (табл. 9.2).
Таблица 9.2 - Таблица истинности функций трех переменных  и
и 
 | 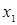 | 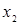 |  |  |
Функция  немонотонная, так как
немонотонная, так как  , а
, а  . Функция
. Функция  монотонна, т.к.
монотонна, т.к.  для всех пар наборов
для всех пар наборов  .
.
Проверка монотонности функции непосредственно по определению требует анализа таблицы функции и может оказаться достаточно громоздкой. Поэтому воспользуемся следующей теоремой.
Теорема.
Всякая булева формула, не содержащая отрицаний, представляет монотонную функцию, отличную от 0 и 1, и наоборот, для любой монотонной функции, отличной от 0 и 1, найдется представляющая её булева формула без отрицаний.
Следствие.
Сокращенная ДНФ монотонной функции является её минимальной ДНФ.
Пример.
Определить, является ли функция  монотонной.
монотонной.
Выразим  через элементарные функции булевой алгебры:
через элементарные функции булевой алгебры:
 .
.
Полученная формула булевой алгебры не содержит отрицаний, следовательно, функция  является монотонной.
является монотонной.
9.2.2 Замкнутые классы булевых функций
Рассмотрим понятия замыкания и замкнутого класса.
Определение.
Пусть  - некоторое подмножество функций из
- некоторое подмножество функций из 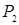 . Замыканием множества
. Замыканием множества  булевых функций называется множество
булевых функций называется множество 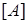 , состоящее из функций, представимых в виде формул через функции множества
, состоящее из функций, представимых в виде формул через функции множества  .
.
Пример.
а)  , очевидно
, очевидно  ;
;
б)  , замыканием этого множества будет класс
, замыканием этого множества будет класс 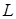 всех линейных функций, то есть функций, имеющих вид:
всех линейных функций, то есть функций, имеющих вид:  , где
, где  .
.
Определение.
Класс (множество) называется замкнутым классом, если 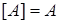 .
.
Пример.
а) класс  − замкнутый класс;
− замкнутый класс;
б) класс  не замкнут;
не замкнут;
Всякий класс 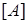 будет замкнутым.
будет замкнутым.
Определение.
Важнейшими замкнутыми классами булевых функций, которые называются классами Поста, являются:
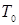 − класс функций, сохраняющих 0;
− класс функций, сохраняющих 0;
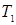 − класс функций, сохраняющих 1;
− класс функций, сохраняющих 1;
 − класс самодвойственных функций;
− класс самодвойственных функций;
 − класс монотонных функций;
− класс монотонных функций;
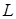 − класс линейных функций.
− класс линейных функций.
Булева функция  может принадлежать одному или нескольким классам Поста, а может не входить ни в один класс.
может принадлежать одному или нескольким классам Поста, а может не входить ни в один класс.
Пример.
Функция  входит в класс линейных функций
входит в класс линейных функций 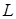 и в класс функций, сохраняющий 1. Функция
и в класс функций, сохраняющий 1. Функция  принадлежит всем классам. Функция штрих Шеффера
принадлежит всем классам. Функция штрих Шеффера  не входит ни в один из классов.
не входит ни в один из классов.
Теорема 9.1Каждый из классов Поста замкнут.
Замкнутые классы Поста попарно различны.
В табл. 9.3 приведем результаты исследования на принадлежность классам Поста каждой булевой функции двух переменных.
Таблица 9.3 − Принадлежность булевых функций классам Поста
| Булева функция | Формула | Классы Поста | ||||
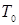 | 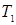 |  |  | 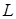 | ||
| Константа 0 | * | - | - | * | * | |
| Конъюнкция |  | * | * | - | * | - |
| Отрицание импликации |  | * | - | - | - | - |
| Повторение первого аргумента |  | * | * | * | * | * |
| Отрицание обратной импликации |  | * | - | - | - | - |
| Повторение второго аргумента |  | * | * | * | * | * |
| Сумма по модулю 2 |  ) ) | * | - | - | - | * |
| Дизъюнкция | 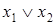 | * | * | - | * | - |
| Стрелка Пирса |  | - | - | - | - | - |
| Эквиваленция |  | - | * | - | - | * |
| Отрицание второго аргумента |  | - | - | * | - | * |
| Обратная импликация |  | - | * | - | - | - |
| Отрицание первого аргумента |  | - | - | * | - | * |
| Импликация |  | - | * | - | - | - |
| Штрих Шеффера |  | - | - | - | - | |
| Константа 1 | - | * | * | * |
9.2.3 Понятия функциональной полноты булевых функций
Понятие полноты булевых функций имеет существенное практическое значение прежде всего в синтезе логических схем, где системе логических функций соответствует набор (серия) типовых логических элементов, а полнота системы означает возможность реализовать с помощью элементов данной схемы любые логические функции.
Определение.
Система функций 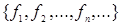 из
из 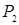 , которое является множеством всех возможных булевых функций, зависящих от любого числа переменных, называется функционально полной, если любая булева функция может быть записана в виде формулы через функции этой системы (в виде суперпозиции функций из этой системы).
, которое является множеством всех возможных булевых функций, зависящих от любого числа переменных, называется функционально полной, если любая булева функция может быть записана в виде формулы через функции этой системы (в виде суперпозиции функций из этой системы).
Пример.
Рассмотрим примеры полных и неполных систем:
а) система 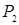 - множество булевых функций, является полной системой;
- множество булевых функций, является полной системой;
б) система  представляет полную систему;
представляет полную систему;
в) система  не является полной.
не является полной.
Теорема 9.1
Пусть даны две системы функций  и
и  из
из 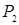 , относительно которых известно, что
, относительно которых известно, что  является полной и каждая её функция выражается в виде формулы через функции системы
является полной и каждая её функция выражается в виде формулы через функции системы  . Тогда система
. Тогда система  также является полной.
также является полной.
Опираясь на эту теорему, можно установить полноту ряда систем следующим образом:
а) представить (задать) функции  в виде формул;
в виде формул;
б) все операции в  заменить формулами над
заменить формулами над  .
.
Пример.
а) системы функций  и
и  являются полными. Доказать, что система
являются полными. Доказать, что система  также является полной.
также является полной.
Действительно, из законов де Моргана и двойного отрицания следует, что в каждой из этих двух систем недостающая до  функция выражается через остальные две:
функция выражается через остальные две:  ,
,  . Следовательно, булева формула
. Следовательно, булева формула  в системе
в системе  перейдет в формулу
перейдет в формулу  , а в системе
, а в системе  - в формулу
- в формулу  .
.
Определение.
Система функций 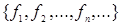 из
из 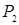 , суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1, называется ослаблено функционально полной или функционально полной в слабом смысле.
, суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1, называется ослаблено функционально полной или функционально полной в слабом смысле.
В терминах замкнутого класса можно дать следующее определение полноты.
Определение.
Система булевых функций  называется функционально полной, если
называется функционально полной, если  .
.
Исходя из рассмотренных определений можно предположить, что не каждая система является полной. Пост предложил и исследовал условия, называемые критерием полноты, выполнение которых позволяет определить, является ли произвольная система булевых функций полной в сильном смысле.
Рассмотрим теорему полноты Поста, которая является основной теоремой о функциональной полноте булевых функций.
9.2.4 Теорема Поста о функциональной полноте
Для того чтобы система функций  была функционально полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию, не сохраняющую ноль, хотя бы одну функцию, не сохраняющую единицу, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию, хотя бы одну нелинейную функцию.
была функционально полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию, не сохраняющую ноль, хотя бы одну функцию, не сохраняющую единицу, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию, хотя бы одну нелинейную функцию.
Одна и та же функция может представлять в функционально полной системе одно или несколько требуемых свойств, а также может обладать всеми пятью требуемыми свойствами. Следовательно, минимальное число булевых функций в функционально полном наборе равно единице.
Если каждая из взятых функций обладает лишь одним свойством (но каждая другим), то для функциональной полноты необходима система из 5-ти функций.
Говорят, что функционально полная система функций образует базис в логическом пространстве.
Определение.
Система функций называется минимально полным базисом, если удаление из неё любой функции превращает эту систему в неполную.
Определение.
Полная система булевых функций называется несократимой, если из неё нельзя исключить ни одной булевой функции без потери свойств полноты.
В связи с тем, что каждая из функций может обладать несколькими свойствами, функционально полные системы могут быть построены с помощью одной, двух, трех и четырех функций.
Пример.
Наиболее распространенная система − система из трех функций: отрицание, конъюнкция и дизъюнкция. С помощью этих функций могут быть описаны процессы управления любыми производственными процессами; функция, описывающая работу любого устройства вычислительной системы и т.п.
Пример.
Определить с помощью теоремы Поста, является ли система  функционально полной?
функционально полной?
Операцию отрицания можно представить полиномом Жегалкина в виде  , следовательно, функция отрицания линейна. Функция отрицания является самодвойственной, не сохраняет), не сохраняет 1(определяется с использованием таблицы истинности), немонотонна. Импликация является нелинейной функцией, т.к. её полином Жегалкина имеет вид
, следовательно, функция отрицания линейна. Функция отрицания является самодвойственной, не сохраняет), не сохраняет 1(определяется с использованием таблицы истинности), немонотонна. Импликация является нелинейной функцией, т.к. её полином Жегалкина имеет вид  , она несамодвойственная, не сохраняет 0 , сохраняет 1 (можно определить по таблице истинности), немонотонна. Следовательно, для каждого класса Поста в данной системе имеется хотя бы одна функция, которая этому классу Поста не принадлежит. По теореме Поста такая система булевых функций является функционально полной.
, она несамодвойственная, не сохраняет 0 , сохраняет 1 (можно определить по таблице истинности), немонотонна. Следовательно, для каждого класса Поста в данной системе имеется хотя бы одна функция, которая этому классу Поста не принадлежит. По теореме Поста такая система булевых функций является функционально полной.
Теорема 9.2
Для того чтобы система функций  была функционально полной в слабом смысле, необходимо и достаточно, чтобы она содержала хотя бы одну немонотонную и хотя бы одну нелинейную функцию.
была функционально полной в слабом смысле, необходимо и достаточно, чтобы она содержала хотя бы одну немонотонную и хотя бы одну нелинейную функцию.
Пример.
Система  функционально полна в слабом смысле, так как конъюкнция нелинейно, а сумма по модулю 2 немонотонна. Константа 0 получается из соотношения
функционально полна в слабом смысле, так как конъюкнция нелинейно, а сумма по модулю 2 немонотонна. Константа 0 получается из соотношения  , однако константу 1 с помощью конъюнкции и суммы по модулю 2 получить нельзя, поэтому
, однако константу 1 с помощью конъюнкции и суммы по модулю 2 получить нельзя, поэтому  не является полной в обычном (полном) смысле. Использование константы 1, которое разрешается определением слабой полноты, сводит
не является полной в обычном (полном) смысле. Использование константы 1, которое разрешается определением слабой полноты, сводит  к полной в сильном смысле системе
к полной в сильном смысле системе  .
.
9.3 Контрольные вопросы и задания
1. Перечислите основные типы булевых функций.
2. Дайте определение булевых функций, сохраняющих 0 и 1.
3. Какое количество всех функций  переменных сохраняет константу 0 и константу 1?
переменных сохраняет константу 0 и константу 1?
4. Какая функция называется монотонной?
5. Как по виду ДНФ булевой функции можно определить, монотонна функция или нет?
6. Поясните структуру алгебры Жегалкина.
7. Перечислите основные законы и тождества алгебры Жегалкина.
8. Определите понятие полинома Жегалкина.
9. Дайте определение линейности булевой функции.
10. Приведите примеры линейных и нелинейных функций двух переменных.
11. Перечислите важнейшие замкнутые классы булевых функций.
12. Какая система булевых функций называется функционально полной?
13. Сформулируйте теорему о полноте двух систем булевых функций.
14. Дайте определение функциональной полноты в слабом смысле.
15. Какая полная система булевых функций является несократимой.
16. Сформулируйте теорему Поста о полноте булевых функций.
Лекция 10. Логика высказываний. Алгебра высказываний.
10.1 Высказывания (основные понятия)
С древнейших времен человечеству известна логика, или искусство правильно рассуждать, причем способность к рассуждениям − это именно искусство. Имея какие-то утверждения (посылки), истинность которых проверена, скажем, на опыте, логик путем умозрительных построений приходит к другому утверждению (заключению), которое также оказывается истинным (в некоторых случаях). Опыт древних (число наблюдательный) был систематизирован Аристотелем, рассмотревшим конкретные виды рассуждений, которые назвал силлогизмами. Однако логика Аристотеля − это классическая логика, то есть наука, традиционно относящаяся к гуманитарному циклу.
Предметом этого раздела дисциплины «Дискретная математика» являются некоторые элементы логики математической.
